算法整理——非对称密钥加密RSA数学相关与简单实现

RSA

   RSA公钥加密算法是1977年由Ron Rivest、Adi Shamir和Leonard Adleman一起提出的，是目前最有影响力的公钥加密算法，能够抵抗到目前为止已知的绝大多数密码攻击。RSA算法基于一个十分简单的数论事实：将两个大质数相乘十分容易，但是想要对其乘积进行因式分解却极其困难。RSA算法是第一个能同时用于加密和数字签名的算法，也易于理解和操作。加密方式是发送者采用接收者的公钥加密，而这个公钥是公开的，任何人都可以知道。接收者利用自己私钥对密文进行解密，因为私钥只有自己知道，此时别人拿到密文以及公钥都无法解出原文。签名方式则反过来，签名者使用私钥签名，查看者只需要使用公钥进行解密。一旦解出的原文消息符合预期，签名者则无法反驳自己曾对这段密文进行签名，因为私钥只有它自己有。

数学基础

欧拉定理

RSA算法的理论基础基于以下的数学推导式

什么情况下(e1, e2, n 关系)才能使得最后一个式子成立？欧拉定理给出了答案：

 欧拉定理表明，若 n, a为正整数，且 互素，则有

 

（欧拉函数φ(n)：在数论，对正整数n，欧拉函数是小于n的数中与n互质的数的数目。）

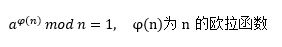
关于欧拉定理的证明，来自 某百科

将1~n中与n互质的数按顺序排布：x1, x2, ……, xφ(n) （显然，共有φ(n)个数）

我们考虑这么一些数：
m1=a*x1, m2=a*x2, m3=a*x3, ……, mφ(n)=a*xφ(n)

1）这些数中的任意两个都不模n同余，因为如果有mS≡mR (mod n) （这里假定mS更大一些），就有：
mS-mR=a(xS-xR)=qn（q为一整数，两者模n同余，在相减之后余数减去，剩余部分将是n的倍数），即n能整除a(xS-xR)。但是a与n互质，a与n的最大公因子是1（此时最小公倍数为a*n），而xS-xR<n（xS, xR均在1~n中），因而左式不可能被n整除。也就是说这些数中的任意两个都不模n同余，φ(n)个数有φ(n)种余数。

2）这些数除n的余数都与n互质，因为如果余数与n有公因子r，那么a*xi=pn+qr=r(……)（这样，a*xi 与 n也将有公因子r），a*xi与n不互质&#