算法学习笔记之计算几何--平面凸包

Introduction

凸包（Convex Hull）是计算几何中的一类极其重要的问题，计算几何中的很多问题都可以转化为凸包问题来解决。

直观的来讲，凸包就像是在一块钉有若干个钉子的木板上撑开一根橡皮筋来讲所有钉子围起来一样。

构造凸包的算法可谓汗牛充栋，著名的有Gift wrapping（Jarvis March算法）, Graham scan, QuickHull, Divide and conquer, Incremental convex hull algorithm等。本文不可能面面俱到，在这里只选取一些具有代表性的算法来阐释凸包构造过程中的基本思想。

下面所介绍的算法中基本上都体现出了一个特征，就是利用问题的集合特质将问题一步步的转化，大事化小，小事化了，从而使问题得到解决。

基于极点的算法

极点

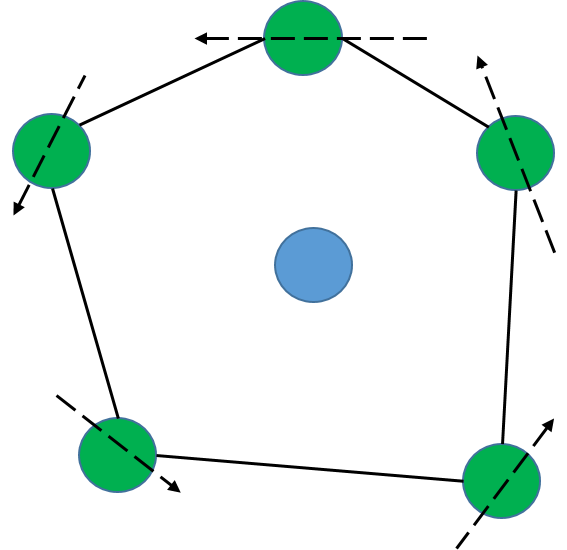
设$S$为平面点集，若存在一条经过点$p$的直线$l$使得除$p$点外所有的点都位于直线$l$的同一端，那么称点$p$为极点（Extreme Point）。否则称为非极点（Non-Extreme Point）。

如上图所示，直观的来讲，一个点是极点那么它一定就是凸包上的点。

构造策略

回忆一下冒泡排序的原理：

一个序列有序当且仅当每一个点都是有序的

同样的根据极点的概念我们有如下的凸包定义：

一个多边形为凸包当且仅当所有顶点都是极点

根据极点的定义我们可以想出一个很直接的凸包的构造算法：遍历每个点，检查是否为极点，如果是，就将它加入到凸包的集合中。这样，构造凸包的问题就被我们转化为了判断点是否为极点的问题，虽然离我们的目标还有一些距离，但已经前进了一大步。不过，我们还没有判断极点的算法。

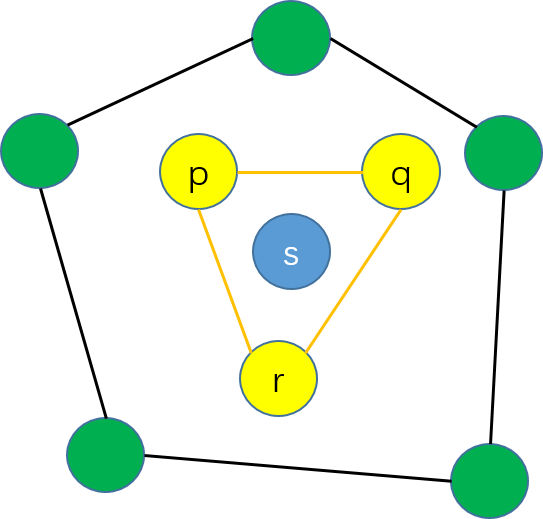
要判断一个点是不是极点其实很容易，它要不是极点，那么一定能找到三个点（从给定的点集中）将它包围起来。原因很简单，因为平面点集的凸包就是能将所有点包围起来的凸多边形，那么对于在凸包内部的点（不是极点的点）最少最少能从凸包上找到三个点将其围起来。于是就有：

平面点集$S$中的一个点$s$不是极点当且仅当存在$\{p,q,r\} \subseteq S \backslash \{s\}$使得$s \in \triangle(p,q,r)$，其中$\triangle(p,q,r)$代表$p,q,r \subseteq S$组成的封闭三角形。

In-Triangle Test

虽然有了上面的判断极点的In-Triangle Test方法，但我们还无法马上给出一个实现，因为我们还不知道如何判断点是不是在三角形内。

要判断点是否在三角形内，需要用到一个计算几何中十分常用而重要的技术，叫做To-Left测试。

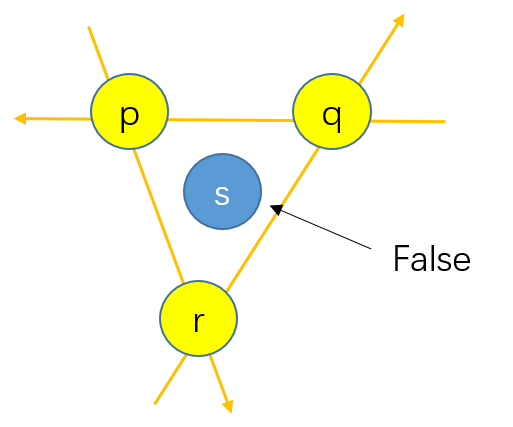
观察上面的图片，如果我们按照一定的顺序（如顺时针）检查三个点$p,q,r$构成的有向线段，就会发现无论是对于有向线段$rq$还是$qp$和$pr$，点$s$都位于它们的左边。

To-Left测试则可以完成这样的任务，对于点$(a, b, s)$，当$s$位于有向线段$ab$的左侧时，ToLeft(a, b, s)返回True，否则返回False。其利用的原理是叉积。

叉积（又称外积），其集合意义是向量$\vec {p1}$和$\vec {p2}$构成的平行四边形的有向面积。同时，当$\vec {p1} \times \vec {p2} > 0$时，$\vec {p1}$位于$\vec {p2}$的顺时针方向，反之$\vec {p1}$位于 p2