图的简单总结

图的简单总结

本文主要根据《数据结构（Java版）》（第3版） 叶核亚 简单总结得到

图

图的术语

线性表中的元素具有线性关系，每个元素只有一个直接前驱和一个直接后继。树形结构中的元素之间具有明显的层次关系，每个元素只有一个前驱和若干个后继，元素之间是非线性关系。图中元素之间具有多对多的非线性关系，图中每个元素可以有多个前驱和多个后继，任意两个元素都可以相邻，图结构比树和线性表更加复杂。

1. 图是由顶点集合以及顶点间的关系集合组成的一种数据结构。顶点之间的关系称为边。一个图G记为$G=(V,E)$，V是顶点的有限集合，E是边的有限集合。
2. 无向图中的边没有方向，每条边用两个顶点的无序对$(v_i,v_j)$表示
3. 有向图中的边有方向，每条边用两个顶点的有序对 <vi,vj> <script type="math/tex" id="MathJax-Element-310"> </script>表示
4. 简单图：在图中，如果不存在顶点到其自身的边，且同一条边在图中不重复出现，称为简单图。
5. 完全图：图中的边数达到最大。无向图中每两个顶点之间都存在边，有n个顶点的无向完全图中有$n*(n-1)/2$条边。有向图中，每两个顶点之间都存在方向相反的两条边，有n个顶点的有向完全图中有$n*(n-1)$条边。
6. 带权图：图中的边具有权值。在不同的应用中，权值有不同的含义。例如，如果顶点表示城市，两个顶点之间边的权值可以表示两个城市之间的距离。
7. 子图：有两个图$G=(V,E)$和$G'=(V',E')$，如果$V'\subseteq V,E'\subseteq E$,则称$G'$是$G$的子图。
8. 邻接顶点：如果$(v_i,v_j)$是无向图中的一条边，则称$v_i$和$v_j$互为邻接顶点。如果 <vi,vj> <script type="math/tex" id="MathJax-Element-321"> </script>是有向图中的一条边，则称 $v_i$邻接到 $v_j$
9. 顶点的度：与顶点$v_i$关联的边数，记为$degree(v_i)$。度为0的点称为孤点。度为1的点称为悬挂点。在无向图中，边数是各顶点度数和的一半。在有向图中，度=入度+出度，$v_i$的入度数是以$v_i$为终点的边数，初度是以$v_i$为起点的边数，图中总边数等于各顶点度数和。
10. 路径：在图$G=(V,E)$中，如果存在顶点序列$(v_i,v_{p1},v_{p2},...,v_{pm},v_j)$，且边$(v_i,v_{p1}),(v_{p1},v_{p2}),...,(v_{pm},v_j)$都是图G的边，则称顶点序列$(v_i,v_{p1},v_{p2},...,v_{pm},v_j)$是一条路径。对于不带权的图，路径长度是指该路径上的边数，对于带权图，路径长度值该路径上各条边的权值之和。简单路径是路径上个各顶点互不重复。回路指起点和终点相同且长度大于1的简单路径。
11. 连通性：在无向图中，如果从顶点到顶点有路径，则称两个顶点连通，如果图中任意两个顶点都是连通的，则称该图为连通图，无向图中的极大连通子图称为该图的连通分量。在有向图中，如果每对顶点之间都存在两条方向相反的路径，则称该图是强连通的。有向图的极大强连通子图称为 该图的强联通分量。
12. 连通图的生成树:连通图首先是无向图，连通的无回路的无向图称为树。树中无回路且连通，如果去掉树中如意一条边，则变为森林，加上一条边则构成回路。一棵树有n个顶点，则有n-1条边。连通图的生成树是图的连通无回路子图。一个非联通无向图，其各连通分量的生成树组成该图的生成森林。
13. 最小生成树：设$G$是一个带权连通无向图，$w(e)$是边$e$的权，$T$是$G$的生成树，$T$中各边的权重之和$w(T)=\sum_{e\in T}w(e)$称为生成树$T$的权。最小生成树是权重最小的生成树。
14. 最短路径：设$G=(V,E)$是一个带权图，若$G$中从顶点$v_i$到$v_j$的一条路径$(v_i,...,v_j)$，其路径长度是所有从$v_i$到$v_j$的路径中的最小值，则$(v_i,...,v_j)$是从$v_i$到$v_j$的最短路径，$v_i$称为源点，$v_j$称为终点。

图的存储结构

存储一个图包括存储图的顶点集合和边集合。通常采用顺序表存储图的顶点集合，而边集合有邻接矩阵和邻接表两种存储结构。

邻接矩阵

邻接矩阵是表示图中各顶点之间邻接关系的矩阵。根据边是否带权值，分为两种形式。

• 不带权图的邻接矩阵：设图$G=(V,E)$有n个顶点，$V=[v_0,v_1,...,v_{n-1}]$，$E$可用一个$n*n$的矩阵描述，矩阵中元素为$a_{ij}$，如果$(v_i,v_j)\in E$或 <vi,vj>∈E <script type="math/tex" id="MathJax-Element-359"> \in E</script>， $a_{ij}=1$，否则 $a_{ij}=0$。无向图的邻接矩阵是对称的。有向图的邻接矩阵不一定对称。从邻接矩阵可知顶点的度。无向图中，邻接矩阵第i行或第i列元素之和是顶点 $v_i$的度。有向图中，邻接矩阵第i行上元素之和是顶点 $v_i$的出度，第i列上元素之和是顶点 $v_i$的入度。
• 带权图的邻接矩阵：设图$G=(V,E)$有n个顶点，$V=[v_0,v_1,...,v_{n-1}]$，$E$可用一个$n*n$的矩阵描述，矩阵中元素为$a_{ij}$，如果$(v_i,v_j)\in E$或 <vi,vj>∈E <script type="math/tex" id="MathJax-Element-371"> \in E</script>，且 $v_i\ne v_j$， $a_{ij}=w_{ij}$，如果 $(v_i,v_j)\in E$或 <vi,vj>∈E <script type="math/tex" id="MathJax-Element-375"> \in E</script>，且 $v_i=v_j$， $a_{ij}=0$。否则 $a_{ij}=\infty$。

图的连接矩阵存储了任意两个顶点间的邻接关系或权值，能够实现各种操作。判断两个顶点是否邻接、获取与设置边的权值等操作时间复杂度为O(1)，但是增加或删除边，需要移动大量元素，效率很低。另外在图的邻接矩阵中，如果两个点之间没有边，矩阵相应位置也存储了元素，对于稠密图，存储效率较高，但是对于稀疏图，存储效率较低，此时需要用邻接链表。

邻接链表

图的邻接链表，采用顺序表存储顶点集合，采用链表存储和一个顶点相关的多条边的信息。每一个顶点和其邻接的边构成一个元素，存储在线性表中，这个线性表即为邻接链表。

以加权有向图为例，邻接链表是一个线性表，其中每个元素有三个域构成，顶点的序号，顶点的值，和顶点相连的边构成的链表。其中加权图有向边也包含三个域，起点的序号，终点的序号，权值。

关于图的算法

图中的算法可以分成三大类：图的遍历，图的最小生成树算法和最短路径算法。

图的遍历

图的遍历是指从图$G$中任意一点$v_i$出发，沿着图中的边前行，到达并访问图中的所有顶点，并且每个顶点只访问一次。遍历图比遍历树更复杂，需要考虑以下三个问题：

1. 指定遍历的第一个访问顶点
2. 由于一个顶点可能与多个顶点相邻，因此要在多个邻接顶点之间约定访问次序
3. 由于图中可能存在回路，在访问某个顶点之后，可能沿着某条路径又回到该顶点。因此，为了避免重复访问同一顶点，在遍历过程中必须对访问过的顶点做标记

根据第2条中访问次序的不同，图的遍历有两种操作：深度优先搜索和广度优先搜索。

图的深度优先搜索遍历

图的深度优先搜索(DFS)的策略是：访问某个顶点$v_i$，寻找$v_i$的一个邻接顶点$v_j$访问，再寻找$v_j$的一个邻接顶点$v_k$访问，如此反复执行，走过一条较长的路径到达最远的顶点。如果顶点$v_k$没有未被访问的其他邻接顶点，则退回到前一个被访问的顶点，再寻找其他访问路径。

图的深度优先搜索遍历算法有递归和非递归两种：

1. 递归版本：从图中一个顶点$v_i$出发的一次深度优先搜索遍历算法描述如下

   • 访问顶点$v_i$，标记$v_i$为已访问状态
   • 选定$v_i$的一个未被访问的邻接顶点$v_j$，从$v_j$开始进行深度优先搜索，递归算法
   • 如果和$v_j$邻接的所有顶点都是已访问状态，则退回到$v_i$
   • 如果$v_i$仍有未被访问的下一个邻接顶点$v_k$,则从$v_k$出发继续搜索；否则由顶点$v_i$出发的一次搜索结束

2. 非递归版本：从图中一个顶点$v_i$出发的一次深度优先搜索遍历算法描述如下

   • 初始化一个栈

   • 访问$v_i$，标记$v_i$为已访问状态，并将$v_i$入栈

   • 重复以下操作，直到栈为空

     取栈顶元素但不出栈

     如果该顶点有一个未被访问的邻接顶点$v_j$，则访问顶点$v_j$，标记$v_j$为已访问状态，并入栈

     否则该顶点出栈

对于一个联通无向图或者一个强联通有向图，从一个顶点出发一次遍历就可以访问图中所有顶点。对于一个非联通无向图或者非强联通有向图，从一个顶点出发的一次遍历只能访问图中的一个联通分量。因此遍历一个非连通图需要遍历各个连通分量。

图的广度优先搜索遍历

广度优先搜索(BFS)的策略是：访问某个顶点$v_i$，接着访问$v_i$所有的未被访问的邻接顶点$v_j,v_k,v_t,...$，再依次访问$v_j,v_k,v_t,...$的所有未被访问的邻接顶点，如此反复执行，直到访问完图中所有顶点。图的广度优先搜索类似于树的层次遍历。

图的广度优先搜索遍历算法一般只用非递归方法：

从图中一个顶点$v_i$出发的一次广度优先搜索遍历算法描述如下

• 初始化一个队列

• 将$v_i$入队，标记$v_i$为已入队状态

• 重复以下操作，直到队列为空

  队头元素出队，访问，找到该顶点所有未入队的邻接顶点，依次入队，并标记为已入队状态

因为所有如果的顶点都能够被访问，所以这里标记的是顶点是否入队的状态，和深度优先遍历不同。

和深度优先搜索一样，对于一个联通无向图或者一个强联通有向图，从一个顶点出发一次遍历就可以访问图中所有顶点。对于一个非联通无向图或者非强联通有向图，从一个顶点出发的一次遍历只能访问图中的一个联通分量。因此遍历一个非连通图需要遍历各个连通分量。

最小生成树

按照生成树的定义，n个顶点的连通无向图的生成树有$n-1$条边。因此，构造最小生成树的准则有以下三条：

1. 必须使用该图中的边来构造最小生成树
2. 必须使用且仅使用$n-1$条边来连接图中的n个顶点
3. 不能使用产生回路的边

构造最小生成树主要有两种方法：Prim算法和Kruskal算法。这两种算法都是基于最小生成的MST性质。

MST性质：设$G=(V,E)$是一个连通带权无向图，$TV$是顶点集合$V$的非空真子集。如果$(tv,v)$是一条权值最小的边，其中$tv\in TV,v\in V-TV$，则必定存在$G$的一棵最小生成树$T$，$T$包含边$(tv,v)$。

Prim

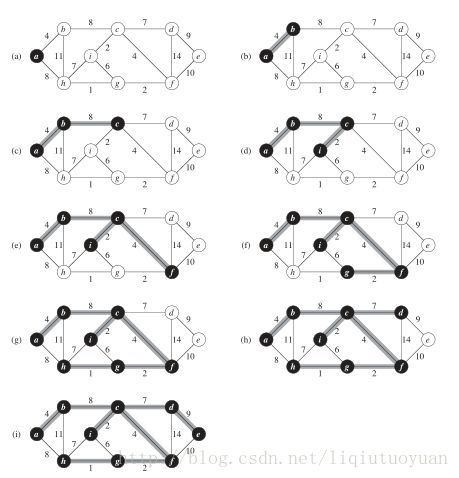
以《算法导论》上368页的一个例子说明Prim算法的过程。

设上图是图$G=(V,E)$，最小生成树$T=(TV,TE)$。

1. 最初$T$中只有一个顶点$a$，没有边，$TV=\{A\},TE=\{\},V-TV=\{b,c,d,e,f,g,h,i\}$
2. 在所有的$tv\in TV,v\in V$的边$(tv,v)\in E$中，选择权值最小的边加入$T$中。在上图，一个顶点在$TV$中，另一个顶点在$V-TV$中的边有$\{(a,b),(a,h)\}$，其中权值最小的边为$(a,b)$，将顶点$b$和边$(a,b)$加入最小生成树$T$中，得到$TV=\{a,b\},TE=\{(a,b)\},V-TV=\{c,d,e,f,g,h,i\}$，此时生成树的权值为4
3. 在所有的$tv\in TV,v\in V$的边$(tv,v)\in E$中，选择权值最小的边$(b,c)$加入$TE$,将$c$加入$TV$，此时$TV\{a,b,c\},TE=\{(a,b),(b,c)\},V-TV=\{d,e,f,g,h,i\}$。重复以上步骤，依次加入的边为$\{(c,i),(c,f),(i,g),(g,h),(c,d),(d,e)\}$，$TV$中的顶点也不断增加。当$TV=V$时，$T=(TV,TE)$就是一颗最小生成树。

Prim算法的描述如下：设$T_i$表示有i个顶点的最小生成树

1. 最初$T_1$只有一个顶点，没有边，即$TV=\{v_0\},TE=\{\},w(T_1)=0$
2. 如果对于$T_i$有$w(T_i)=\sum_{e\in TE}$最小，在所有$tv\in TV,v\in V-TV$的边$(tv,v)\in E$中，选择权值最小的一条边$(tv_i,v_i)$加入$T_i$得到$T_{i+1}$，根据MST性质，$w(T_{i+1})=w(T_i)+(tv_i,v_i)$最小
3. 重复执行步骤2，直到$TV=V$

在实现Prim算法是需要设置一个大小为$n-1$的数组记录从$TV$到$V-TV$具有最小权值的边。

Kruskal

Kruskal算法也是根据MST特性，采用贪心策略逐步求解，每次选择权值最小的且不产生回路的一条边加入生成树，直到加入$n-1$条边。可以看出，用Kruskal算法构造最小生成树主要有两点：1、如何找到权值最小的边；2、如何判断没有生成回路。

Kruskal算法构造加权无向图的算法描述如下：设$G=(V,E)$是有n个顶点的加权无向图，$T=(TV,TE)$是最小生成树

1. 最初$TV=T,TE=\{\}$，即$T$有$G$的n个顶点却没有边，每个顶点构成一个联通分量
2. 选择权值最小的一条边$(u,v)\in E$，并且该边的两个顶点$u,v$分别属于两个联通分量，将此边加入$TE$，并合并$u,v$所在的两个联通分量；如果$u,v$在同一个联通分量中，则放弃该条边
3. 重复执行步骤2，直到$TE$中有$n-1$条边或所有顶点处于一个连通分量中

因为Kruskal算法是根据权值大小选择边的，所以当图中有权值相同的边时，最小生成树不唯一。

在实现过程中，所有边的集合是一个成员变量，通过排序可以得到权值最小的边。设置一个数组放置连通标记，标记一样的顶点联通，在循环中更新数组。

最短路径

求最短路径主要依据的是最短路径的最优子结构性质。描述如下：给定带权重的有向图$G=(V,E)$和权重函数$w:E\rightarrow R$。设$p=<v_0,v_1,...,v_k>$为从节点$v_0$到$v_k$的一条最短路径，设$p_{ij}=<v_i,v_{i+1},...,v_j>$是路径$p$的一条子路径，那么$p_{ij}$是从节点$v_i$到$v_j$的一条最短路径。即任一条最短路径的子路径都是最短路径。

另外最短路径中不能有回路。如果有负回路，则无法求出最短路径，如果有正回路，不是最短路径，如果回路的权值为0，则去掉该回路无影响。所以最短路径中没有回路。对于有n个顶点的带权图，其最短路径最多包含$n-1$条边。

Dijkstra算法

Dijkstra算法求解的是带权有向图中单源最短路径的问题，该算法要求图中所有边的权重非负。该算法可以得到指定源点到图中其他各个顶点的最短路径。Dijkstra算法是广度优先搜索的扩展。以源点为中心层层向外扩展，直到求出所有点的最短路径。

问题描述：给定带权有向图$G=(E,V)$，每条边的权重非负，给定源点$v_0$，求$v_0$到其余各顶点的最短路径。

算法描述：给定带权有向图$G=(V,E)$，将其顶点分成两部分，一部分是$S$，表示已经求出最短路径的顶点集合，初始为$S=\{v_0\}$，之后每确定一个顶点的最短路径，将其加入$S$.另一部分是$S$对于$V$的补集$U=V-S$，表示没有确定最短路径的顶点集合。为每一个顶点设置一个当前最小路径长度$dist_i$，初始值为对任意的$v_i\in V,dist_i=w_{0i}$。求出$j=arg\;\min_{v_i\in U}dist_j$，$v_0$到$v_j$的最短路径长度为$dist_j$，将$v_j$加入集合$S$，并从$U$中除去。接下来更新$U$中所有顶点的当前最小路径长度。对任意的$v_k\in U$，如果$dist_j+w_{jk}<dist_k$，则将$dist_k$更新为$dist_j+w_{jk}$.重复以上步骤，直到$U$为空集。

算法步骤：设$G=(V,E)$是有n个顶点的加权无向图，求以$v_0$为源点到其他各点的最短路径

1. 设置$S=\{v_0\},U=V-S,dist_i=w_{0i},i=1,2,...,n-1$。从$U$中所有的顶点中找到$dist_i$最小的值对应的顶点$v_j$，即$j=ara\;\;min_{v_j\in U}dist_j$，$S=\{v_0,v_j\}$，并将$v_j$从$U$中取出；
2. 假设第k步并入$S$的顶点是$v_k$，根据$v_k$对$U$中顶点的$dist_j$更新。对任意的$v_j\in U$，如果$dist_k+w_{kj}<dist_j$，则将$dist_j$更新为$dist_k+w_{kj}$.更新过后重复步骤1，从$U$中找到$dist_j$最小的顶点加入$S$
3. 重复以上步骤，直到$U$为空集

在实现的过程中，需要记录顶点属于哪个集合，记录每个顶点当前最短路径长度以及记录最短路径。利用三个数组vest,path和dist

1. vest[j]==1表示顶点$v_j$在集合$S$中，初始vest[0]=1
2. path[j]表示从源点$v_0$到$v_j$的最短路径$(v_0,...,v_k,v_j)$中$v_k$的序号，即最短路径上$v_j$的前驱
3. dist[j]表示$v_0$到$v_j$的当前最短路径，如果无通路，设置为$\infty$，一般用优先队列实现

Dijkstra算法求解的是从指点源点到图中各点的最短路径，是贪婪算法，在迭代的过程中，每次求出源点到一个顶点的最短距离。如果要求指定两个顶点$v_i,v_j$间的最短距离，以$v_i$为源点进行Dijkstra算法，当$v_j$的最短路径求出时，算法停止。

有向无环图的单源最短路径有线性时间算法，时间复杂度可以达到为$O(V+E)$。对于有环图，Dijkstra的时间复杂度是？，分析如下。

在《算法导论》中，对于Dijkstra算法的描述如下：

Dijkstra(G,s)

1. 初始化源点
2. 设置S为空集
3. 优先队列Q=G.V，将所有顶点加入优先队列
4. while Q非空
5.       u=ectractMin(Q)，取出Q队首元素
6.       将u加入S
7.       对任意的u的邻接顶点v
8.              relax(u,v,w)，相当于更新U中顶点的当前最小路径长度

这里的Dijkstra算法由优先队列辅助实现。在算法中，需要执行三种优先队列的操作，第3行的插入操作(insert)，用所有顶点构造一个优先队列；第5行的取出最小元素(poll)和第8行的更新键值操作(update)。（难点是如何更新键值）。三种操作中插入和取出操作对每个顶点执行一次，一共执行$|V|$次。更新键值在7、8行的循环中，对连接u和v的边也只操作一次，所以一共执行$|E|$次(当图是无向图时，指向2|E|次)。

Dijkstra算法总的运行时间依赖于优先队列的实现。有三种实现方式(和自己实现Dijkstra的过程一样)：

1. 利用数组来实现优先队列。前文中介绍Dijkstra算法时，用数组来存储每个节点的当前最小路径长度。insert和update操作的时间是$O(1)$，poll操作时需要遍历整个数组找到最小值，所以是$O(V)$。总体时间复杂度为$O(V^2+E)$
2. 如果用二叉堆来实现最小优先队列，比如Java中的PriorityQueue。利用V个顶点构造堆的时间复杂度是$O(V)$，每一次poll操作的时间是$O(lgV)$。PriorityQueue中没有关于更新键值的操作，所以需要先remove()再offer()，所以update时间是$O(lgV)$。所以总的时间复杂度为$O(V+VlgV+ElgV)=O((V+E)lgV)$。如果所有节点都可以从源点到达，则$E>V$，时间复杂度可以写作$O(ElgV)$
3. 用斐波那契堆实现，斐波那契堆的构造时间是$O(V)$，poll时间是$O(lgV)$，但是update时间是$O(1)$。总的时间复杂度是$O(V+VlgV+E)$。如果所有节点都可以从源点到达，则$E>V$，时间复杂度可以写作$O(VlgV+E)$。从历史角度来说，斐波那契堆提出的动机就是人们观察到Dijkstra算法调用update操作的次数比poll次数更多，所以任何能将update操作的摊还代价降低到$o(lgV)$而又不增加poll时间的方法都比二叉堆更优。

Dijkstra算法即类似于广度优先搜索，又类似于最小生成树Prim算法。Dijkstra算法本质上是一种广度优先搜索，没有回溯。在广度优先搜索中将遍历过的顶点放在集合S中，这些顶点的广度优先距离已知，正如Dijkstra算法S中顶点的最短路径已知。Dijkstra算法和Prim算法相同点在于，两个算法搜给定初始顶点集合S(Princess算法中是T、E)，用最小优先队列(也可以使用数组存储，然后比较)找到可以加入集合的顶点，并将位于集合外的顶点的权重进行相应的调整。

Floyd算法

Folyd算法是以图的邻接矩阵表示为基础。