算法导论 5.3-3

1 问题

假设不是将元素A[i]与子数组A[i…n]中的随机一个元素相交换，而是将它与数组任何位置上的随机元素相交换：

PERMUTE-WITH-ALL(A)
1    n <- length[A]
2    for i <- 1 to n
3        do swap A[i] <-> A[RANDOM(1, n)]

这段代码会产生均匀随机排列吗？为什么会？或为什么不会？

2 分析与解答

显然代码肯定可以产生A中元素的全排列，但是产生的排列中有一些是相同的，这样就要考察A中元素的每一个全排列的重复次数是否相同，如果相同就能产生，反之就不能。

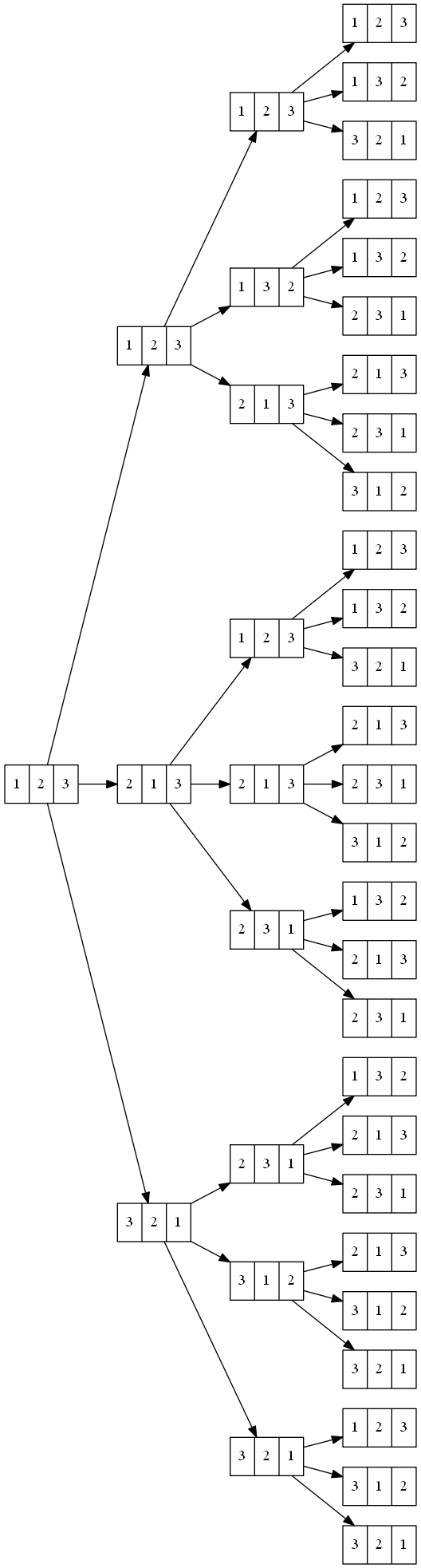
假设A=[1, 2, 3]，那么分析第2，3行的for循环，有下面的产生链：

由图可见，

[1, 2, 3]	4
[1, 3, 2]	5
[2, 1, 3]	5
[2, 3, 1]	5
[3, 1, 2]	4
[3, 2, 1]	4

A中元素的全排列中每一个排列出现的次数是不同的，所以不会产生均匀的随机序列。通过上面的分析，PERMUTE-WITH-ALL(A)会产生nⁿ 个序列，而A中元素的全排列只有n！个，并且nⁿ /n! ，当n>2时，是不可能得到整数的，所以当n>2时，不可能产生出均匀的随机序列。