算法导论 2.3-7

题目

请给出一个运行时间为 的 算法，使之能在给定一个由n个整数构成的集合S和另一个整数x时，判断S中是否存在有两 个其和为x的元素。

分析

要求运行时间为 ,所以想到应该用分治法；因为要求找到某个条件，所以猜测查找过程可能是类似二分查找的某种算法。ps：我们的算法不只希望找到是否存在，还要给出集合中和为x的整数对。

当S是集合时

假设集合中的元素Sx + Sy = x，那么Sx = x - Sy并且Sy = x - Sx。那么对于这样集合S'={S'i | S'i = x - Si, Si 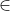S}，有Sx == S'y 且Sy = S'x。这就是这道题的核心算法。另外，需要考虑当Si == x/2的情况，当S中只有一个元素等于x/2，就会成为干扰项，算法中需要将干扰项去掉。这样算法初步成型：

1. 查找Si== x/2的位置
2. 若存在以此位置将S分为两部分(不含Si== x/2的位置)；若不存以中点将S分为两部 分（包含中点）
3. 用x对前一部分的每个元素做差,形成集合S'
4. 对于S'中的每个元素，在S的后半部分中使用二分查找

当S是数组时

由于集合是不包含重复元素的，将此算法扩展到有重复元素的情况，即S是数组的情况。最简单的办法就是扫描一下S，将不等于x/2的重复元 素只保留一个。但我想使用另一种方法，使用这种方法可以将分组与判断x/2结合起来。这种方法基于这个认识：只有在算法的第二步中，重复元素被分在不 同部分时才会干扰判断。

例如，假设一个升序排序的数组S=[1，2，3，4，8，10，10，25]和x=18，若S分 为[1，2，3，4，8]和[10，10，25]这样是不影响查找的。若S分为[1，2，3，4，8， 10]和[10，25]就影响查找了。

所以我们在分组时可以将相同元素分到同一部分， 只需将对集合的算法的第二步分组的条件做小幅修改，即改变为：

• 若Si == x/2存在,以此位置将S分为两部分； 若不存在,以x/2将S分为两部分，前一部分的元素都小于等于x/2，后一部分都大于x/2。

就可以解决将相同元素分在相同组的问题。

通过以上的分析，实际上对于分组的操作可以使用我的博客对习题2.3-6提供的 BINARY-SEARCH-INSERTION 过程。此处需要注意BINARY-SEARCH-INSERTION返回大于等于查询值的位置，为了与之保持一致性所以将等于x/2的元素分到前面的分组，否则主循环边界不好判断。由于重复元素的存在，过程的结果可能产生重复，需要将重复结果去除。

伪代码

1.   BINARY-SEARCH-SUM(S, p, r, x)
   
2.   create 2-d array M[1...]
   
3.   key <- X / 2
   
4.   j = 0
   
5.   q <- BINARY-SEARCH-INSERIONT(S, p, r, key)
   
6.   if S[q] + S[q] == x and (S[q] + S[q-1] == x or S[q] + S[q+1] = x)
   
7.       then j <- j + 1
   
8.            append array [S[q],S[q]] to M[j]
   
9.   while S[q] == key
   
10.       do q <- q+1
    
11.   for i <- q to r
12.       do v = BINARY-SEARCH(S, p, q-1, x - S[i])
    
13.           if v != NIL
    
14.                then j <- j+1
    
15.                         append array [S[v], S[i]] to M[j]
    
16.   create 2-d array Result[1...j]
    
17.   for u <- 1 to j
    
18.       do result[u] <- T[u]
    
19.   remove repeat data in result
20.   return Result[1...j]

从伪代码可知，过程的时间复杂度由11～15行的主循环决定，其中13～15行运行次数是常数，所以过程的运行时间为 ，q-p必然为(r-p)/a，a为大于1的正常数，令(r-p)=n，因为二分查找的时间复杂度为lgn，因此运行时间等价于(1-1/a)nT(n/a)=(1-1/a)nlg(n/a)=bnlgn-bnlga= 。

Python代码实现

def binary_search_sum(s, p, r, x):
    result = []
    key = x / 2
    q = binary_search_insertion(s, p, r, key)
    if s[q] + s[q] == x and (s[q] + s[q + 1] == x or s[q] + s[q - 1] == x):
        result.append([s[q], s[q]])
    while s[q] == key:
        q += 1
     for i in range(q, r + 1):
        k = binary_search(s, p, q-1, x-s[i])
        if k != None:
            result.append([s[k], s[i]])
    for i in range(0, len(result)-1):
        if result[i] == result[i+1]:
            result.remove(result[i])
    return result