这题要用构造法,
n=1特判
考虑n>=2的情况
不难发现最后那个数必须是0,否则无解(因为1和任何数左运算结果为1)
倒数第二个数若为1,则(..1)->0 =0
否则倒数第二个数为0:
此时若倒数第三个数为0 (...(0->0))->0=0 (0->0)
否则倒数第三个数为1 (...(1->0))->0 由于(..1)->0 =0 所以把1右运算 ..->(1->0)=..->0 想让结果为1,则..=0
考虑前面有1个0
(...->(0->(1->1->..->1->0))->0 = (..->(0->0))->0=(..->1)->0=1->0 =0
有解
否则前面均为1
1->1->1->1->0->0 无论怎么括都无解
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
#include<string>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define F (100000007)
#define MAXN (1000000+10)
typedef long long ll;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return (a-b+(a-b)/F*F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
int a[MAXN],n;
char str1[]="YES\n",str2[]="NO\n";
string logic(string s1,string s2)
{
string p=""+s1+"->"+s2+"";
p="("+p+")";
return p;
}
string itos(int x)
{
if (x) return string("1");
return string("0");
}
string logic(int i,int j)
{
string p(itos(a[i]));
Fork(k,i+1,j)
{
p+="->"+itos(a[k]);
}
p="("+p+")";
return p;
}
int main()
{
// freopen("B2.in","r",stdin);
// freopen(".out","w",stdout);
cin>>n;
For(i,n) scanf("%d",&a[i]);
if (a[n]==1)
{
cout<<str2;
return 0;
}
if (n==1)
{
cout<<str1<<"0\n";
return 0;
}
if (a[n-1]==1)
{
string p;
p=logic(logic(1,n-1),"0");
cout<<str1<<p<<endl;
return 0;
}
if (a[n-1]==0)
{
ForD(i,n-2)
if (a[i]==0)
{
string p=logic(i+1,n-1);
p=logic("0",p);
if (i>1) p=logic(logic(1,i-1),p);
p=logic(p,"0");
cout<<str1<<p<<endl;
return 0;
}
}
cout<<str2;
return 0;
}





 本文详细解释了在逻辑表达式中如何正确使用括号来改变运算顺序,确保表达式的值为假。通过实例演示了在没有括号的情况下从左到右计算与括号的存在如何影响最终结果。
本文详细解释了在逻辑表达式中如何正确使用括号来改变运算顺序,确保表达式的值为假。通过实例演示了在没有括号的情况下从左到右计算与括号的存在如何影响最终结果。
 ', and the arguments and the result of the implication are written as '
', and the arguments and the result of the implication are written as '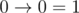
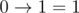
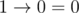
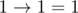
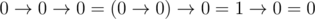 .
.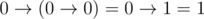 .
.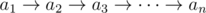 determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement
of brackets.
determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement
of brackets.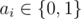 ),
which means the values of arguments in the expression in the order they occur.
),
which means the values of arguments in the expression in the order they occur.
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








