CF 574E(Bear and Drawing-2*n点阵画树)

最新推荐文章于 2024-04-23 16:15:02 发布

nike0good

最新推荐文章于 2024-04-23 16:15:02 发布

阅读量1.4k

点赞数

分类专栏：构造法

本文链接：https://blog.csdn.net/nike0good/article/details/48115749

版权

构造法专栏收录该内容

31 篇文章 2 订阅

订阅专栏

Limak is a little bear who learns to draw. People usually start with houses, fences and flowers but why would bears do it? Limak lives in the forest and he decides to draw a tree.

Recall that tree is a connected graph consisting of n vertices and n - 1 edges.

Limak chose a tree with n vertices. He has infinite strip of paper with two parallel rows of dots. Little bear wants to assign vertices of a tree to some n distinct dots on a paper so that edges would intersect only at their endpoints — drawn tree must be planar. Below you can see one of correct drawings for the first sample test.

Is it possible for Limak to draw chosen tree?

Input

The first line contains single integer n (1 ≤ n ≤ 105).

Next n - 1 lines contain description of a tree. i-th of them contains two space-separated integers ai and bi (1 ≤ ai, bi ≤ n, ai ≠ bi) denoting an edge between vertices ai and bi. It's guaranteed that given description forms a tree.

Output

Print "Yes" (without the quotes) if Limak can draw chosen tree. Otherwise, print "No" (without the quotes).

        Sample test(s) 
      

          input 
        
8
1 2
1 3
1 6
6 4
6 7
6 5
7 8

          output 
        
Yes

          input 
        
13
1 2
1 3
1 4
2 5
2 6
2 7
3 8
3 9
3 10
4 11
4 12
4 13

          output 
        
No

这题要构造解

构造的解是这样的

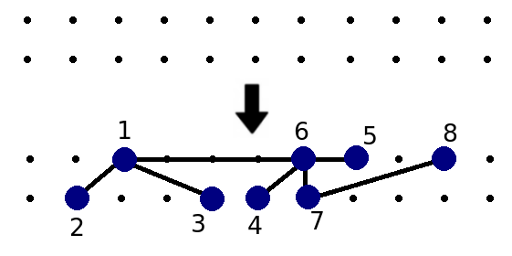
首先我们把叶子节点以及相连的链标记is_lef

然后对每个点统计分出的链的次数(分出一颗大子树不计)

然后除链和Y形，点最多分出2个大子树，否则无解

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Forpiter(x) for(int &p=iter[x];p;p=next[p])  
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define F (100000007)
#define MAXN (200000+10)
typedef long long ll;
ll mul(ll a,ll b){return (a*b)%F;}
ll add(ll a,ll b){return (a+b)%F;}
ll sub(ll a,ll b){return (a-b+(a-b)/F*F+F)%F;}
void upd(ll &a,ll b){a=(a%F+b%F)%F;}
int n;
int edge[MAXN],pre[MAXN],next[MAXN],siz=1;
void addedge(int u,int v) {
	edge[++siz]=v;
	next[siz]=pre[u];
	pre[u]=siz;
}
void addedge2(int u,int v){addedge(u,v),addedge(v,u);}
int degree[MAXN]={0};

bool is_lef[MAXN]={0};
int legs[MAXN]={0};
void dfs(int x,int f)
{
	is_lef[x]=1;
	Forp(x) {
		int v=edge[p];
		if (v==f) continue;
		if (degree[v]<=2) dfs(v,x); //链 
	}
}



int main()
{
//	freopen("E.in","r",stdin);
//	freopen(".out","w",stdout);
	
	MEM(edge) MEM(pre) MEM(next)
	cin>>n;
	For(i,n-1) {
		int u,v;
		scanf("%d%d",&u,&v);
		addedge2(u,v);
		degree[u]++;degree[v]++;
	}
	
	//找链 
	For(i,n) {
		if (degree[i]==1) dfs(i,0);		
	}
	
	
	//找Y型 
	For(i,n) {
		Forp(i) {
			int v=edge[p];
			if (is_lef[v]) ++legs[i]; //一个点连出的链数 
		}
	}
	
	
	bool flag=1;
	
	
	For(i,n) {
		if (is_lef[i]) continue;
		int cnt=0;
		
		Forp(i) {
			int v=edge[p];
			if (!is_lef[v]&°ree[v]-min(legs[v],2)>=2)  //这个邻居不是链也不是Y 
				++cnt;
		} 
		
		
		if (cnt>=3) { //只能向两边 
			flag=0;break;
		}
		
	}
	
	
	
	if (flag) puts("Yes");
	else puts("No");
	
	
	return 0;
}