插入排序及其解决思路
算法的作用自然不用多说,无论是在校学生,还是已经工作多年,只要想在计算机这条道路走得更远,算法都是必不可少的。
就像编程语言中的“Hello World!”程序一般,学习算法一开始学的便是排序算法。排序问题在日常生活中也是很常见的,说得专业点:
输入是:n个数的一个序列 <a1,a2,...,an−1,an> <script type="math/tex" id="MathJax-Element-1"> </script>
输出是:这n个数的一个全新的序列 <a,1,a,2,...,a,n−1,a,n> <script type="math/tex" id="MathJax-Element-2"> </script>,其特征是 a,1≤a,2≤...≤a,n−1≤a,n
举个例子,在本科阶段学校往往要求做的实验中大多是“学生管理系统”、“信息管理系统”、“图书管理系统”这些。就比如“学生管理系统”中的分数,每当往里面添加一个新的分数时,便会和其他的进行比较从而得到由高到低或由低到高的排序。
我本人是不太喜欢做这种管理系统的…… 再举个比较有意思的例子。
大家肯定都玩过扑克牌,撇开部分人不说,相信大部分童鞋都热衷于将牌按序号排好。那么这其中就蕴含着算法的思想:
1)手中的扑克牌有2种可能:没有扑克牌(为空)或者有扑克牌且已排好序。
2)从桌上抓起一张牌后,从左往右(从右往左)依次进行比较,最终选择一个合适的位置插入。简单的说,插入排序的精髓在于“逐个比较”。
在列出代码之前,先来看看下面的第一张图,我画的不是太好,就是有没有经过排序的 “8,7,4,2,3,9”几个数字,根据上面的描述,将排序过程描述为:
1)将第二个数字“7”和“8”比较,发现7更小,
于是将“8”赋值到“7”所在的位置,
然后将7赋值给“8”所在的位置。
2)将”4“移到”7“所在的位置,”7“和”8“后移一位。
3)同样的步骤,将”2“和”3“移到”4“的前面。
4)”9“比前面的数字都大,故不移动。仅仅是这样的描述还是不够的,我们需要更加专业一点。
1)设置一个循环,从第二个数字开始(索引为1)不断与前面的数字相比。
2)每次循环开始时作为比较的数的索引为j,设置temp为其值。(因为在前面也看到了,将”8“赋值到”7“的位置时,如果不将”7“保存起来,那么便丢失了这个数字。)
3)取得j的前一位i。
4)只要i仍在数组中,并且索引为i处的值大于temp,就将i后一位的值设为i处的值,同时将i减1。
5)在i不在数组中或i处的值不必temp大时结束第四部的循环,然后将i后一位的值设置为temp。将上面这部分描述翻译为insertion_sort函数,下面是完整的测试程序。
#include <iostream>
#include <cstdio>
using namespace std;
#define MAX_N 1000
int A[MAX_N];
int n;
void insertion_sort();
int main()
{
printf("数组长度:\n");
scanf("%d",&n);
printf("数组内容:\n");
for(int i=0;i<n;i++)
{
scanf("%d",&A[i]);
}
insertion_sort();
for(int i=0;i<n;i++)
{
printf("%d ",A[i]);
}
return 0;
}
void insertion_sort()
{
for(int j=1;j<n;j++)
{
int temp=A[j];
int i=j-1;
while(i>=0&&A[i]>temp)
{
A[i+1]=A[i];
i=i-1;
}
A[i+1]=temp;
}
}下面是能够帮助我们理解算法的正确性的循环不变式的三条性质:
初始化:循环第一次迭代之前,它为真。
保持:如果循环的某次迭代之前它为真,那么下次迭代之前它仍为真。
终止:在循环终止时,不变式能够提供一个有助于证明算法正确性的性质。就比如上面排序的例子,终止意味着在最后一次迭代时,由传入数组元素构成的子数组元素都已排好序,因此此时子数组就等同与原数组,于是循环终止。
学习如何分析算法
继续分析排序算法,我们知道排序10000个数肯定要比排序10个数所花费的时间更长,但除了输入的项数外就没有其他的影响因素吗?当然有,比如说输入的序列的已被排序的程度,如果是“23456781”这个序列,我们仅仅需要将1放到首位就好,而输入是”87654321“,我们就需要将7到1依次与其前面的数字进行比较。
关于算法的分析也有两个定义:
1)输入规模,当考虑的是排序算法时,那么规模就指的是项数;如果考虑的是图算法,那么规模就是顶点数和边数。
2)运行时间,名义上来说就是算法执行的时间,但实际上我们在分析一个算法时考量的算法执行的操作数或步数。下面我们通过前面排序算法的伪代码来分析它的运行时间。
INSERTION-SORT(A)
1 for j = 2 to A.length // 代价c1,次数n
2 temp=A[j]; // 代价c2,次数n-1
3 // 将A[j]插入到已排序的A[1..j-1] // 代价0,次数n-1
4 i=j-1; // 代价c4,次数n-1
5 while i>0 and A[i]>temp // 代价c5
6 A[i+1]=A[i]; // 代价c6
7 i=i-1; // 代价c7
8 A[i+1]=temp; // 代价c8,次数n-1代价为c1处的次数为n应该比较好理解对吧,从j=1到j=n一共有n步,j=n也应该包括在内,因为这是算法终止的情况。而j=n时,程序直接终止了,所以在代价c2、c3、c7处次数都为n-1。
那么在while循环中呢,代价为c4的时候次数为多少呢,很显然应该是 ∑nj=2tj ,而c5和c6在while循环里总有一次它不会去执行,因此次数为 ∑nj=2(tj−1) 。
将代价和次数相乘,便得到了该算法所需的总时间:
T(n)=c1n+c2(n−1)+c4(n−1)+c5∑nj=2tj+c6∑nj=2(tj−1)+c7∑nj=2(tj−1)+c8(n−1)
除此之外我们还可以来对算法进行最好和最坏情况的分析:
1)在最好情况下,也就是整个输入数组其实都是排好序的,那么它根本没法进入while循环,也就是说当i取初值j-1时,有 A[i]≤temp ,从而对 j=2,3,4...n 都有 tj=1 。
那么算法的总时间也就可以算出来了:
T(n)=(c1+c2+c4+c5+c8)n−(c2+c4+c5+c8)
2)在最坏情况下,也就是数组是逆向排好序的,那么就需要将 A[j] 与已排好序的数组 A[1...j1] 中的每个元素进行比较,从而对 j=2,3,4...n 都有 tj=j 。
那么算法的总时间也就可以算出来了:
T(n)=(c52+c62+c72)n2+(c1+c2+c4+c52−c62−c72+c








 本文深入探讨了算法在计算机科学中的重要性,特别是通过插入排序和分治策略来说明如何分析和设计算法。文章详细介绍了插入排序的工作原理、算法分析、渐近记号(Θ、O、Ω)的概念,以及分治法的基本思想、应用实例(如归并排序和最大子数组问题)。此外,还讨论了递归树在求解递归式中的作用,强调了在分析算法时忽略低阶项和常数的重要性。
本文深入探讨了算法在计算机科学中的重要性,特别是通过插入排序和分治策略来说明如何分析和设计算法。文章详细介绍了插入排序的工作原理、算法分析、渐近记号(Θ、O、Ω)的概念,以及分治法的基本思想、应用实例(如归并排序和最大子数组问题)。此外,还讨论了递归树在求解递归式中的作用,强调了在分析算法时忽略低阶项和常数的重要性。
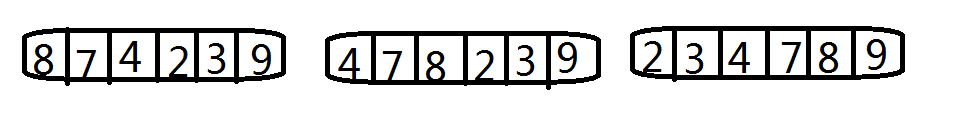
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 149
149

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








