【数据结构与算法】模式匹配——从BF算法到KMP算法（附完整源码）

转载请注明处处：http://blog.csdn.net/ns_code/article/details/19286279

模式匹配

    子串的定位操作通常称为串的模式匹配。模式匹配的应用很常见，比如在文字处理软件中经常用到的查找功能。我们用如下函数来表示对字串位置的定位：

int index(const string &Tag,const string &Ptn,int pos)

    其中，Tag为主串，Ptn为子串（模式串），如果在主串Tag的第pos个位置后存在与子串Ptn相同的子串，返回它在主串Tag中第pos个字符后第一次出现的位置，否则返回-1。

BF算法

    我们先来看BF算法(Brute-Force，最基本的字符串匹配算法)，BF算法的实现思想很简单：我们可以定义两个索引值i和j，分别指示主串Tag和子串Ptn当前正待比较的字符位置，从主串Tag的第pos个字符起和子串Ptn的第一个字符比较，若相等，则继续逐个比较后续字符，否则从主串Tag的下一个字符起再重新和子串Ptn的字符进行比较，重复执行，直到子串Ptn中的每个字符依次和主串Tag中的一个连续字符串相等，则匹配成功，函数返回该连续字符串的第一个字符在主串Tag中的位置，否则匹配不成功，函数返回-1。

    用C++代码实现如下：

/*
返回子串Ptn在主串Tag的第pos个字符后(含第pos个位置)第一次出现的位置，若不存在，则返回-1
采用BF算法，这里的位置全部以从0开始计算为准，其中T非空，0<=pos<=Tlen
*/
int index(const string &Tag,const string &Ptn,int pos)
{
	int i = pos;  //主串当前正待比较的位置，初始为pos
	int j = 0;   //子串当前正待比较的位置，初始为0
	int Tlen = Tag.size();  //主串长度
	int Plen = Ptn.size();  //子串长度
	
	while(i<Tlen && j<Plen)
	{
		if(Tag[i] == Ptn[j])   //如果当前字符相同，则继续向下比较
		{   
			i++;
			j++;
		}
		else   //如果当前字符不同，则i和j回退，重新进行匹配
		{   
			//用now_pos表示每次重新进行匹配时开始比较的位置，则
			//i=now_pos+后移量，j=0+后移量
			//则i-j+1=now_pos+1,即为Tag中下一轮开始比较的位置
			i = i-j+1;
			//Ptn退回到子串开始处
			j = 0;
		}
	}

	if(j >= Plen)
		return i - Plen;
	else
		return -1;
}

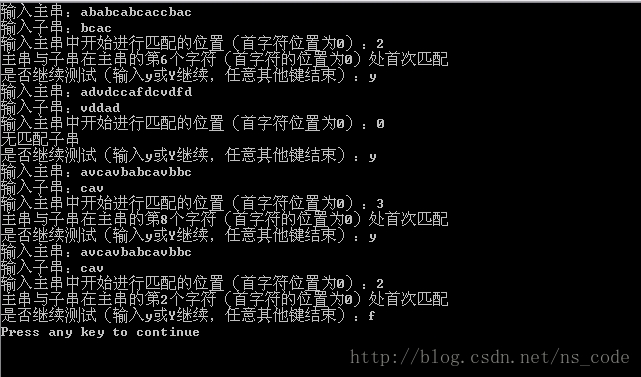
    调用上面的函数，采用如下代码测试：

int main()
{
	char ch;
	do{
		string Tag,Ptn;  
		int pos;
		cout<<"输入主串：";
		cin>>Tag;
		cout<<"输入子串：";
		cin>>Ptn;
		cout<<"输入主串中开始进行匹配的位置（首字符位置为0）：";
		cin>>pos;
	
		int result = kmp_index(Tag,Ptn,pos);
		if(result != -1)
			cout<<"主串与子串在主串的第"<<result<<"个字符（首字符的位置为0）处首次匹配"<<endl;
		else
			cout<<"无匹配子串"<<endl;

		cout<<"是否继续测试（输入y或Y继续，任意其他键结束）：";
		cin>>ch;
	}while(ch == 'y' || ch == 'Y');
	return 0;
}

    测试结果如下：

    以上算法完全可以实现要求的功能 ，而且在字符重复概率不大的情况下，时间复杂度也不是很大，一般为O（Plen+Tlen）。但是一旦出现如下情况，时间复杂度便会很高，如：子串为“111111110”，而主串为 “111111111111111111111111110” ，由于子串的前8个字符全部为‘1’，而主串的的前面一大堆字符也都为1，这样每轮比较都在子串的最后一个字符处出现不等，因此每轮比较都是在子串的最后一个字符进行匹配前回溯，这种情况便是此算法比较时出现的最坏情况。因此该算法在最坏情况下的时间复杂度为O（Plen*Tlen），另外该算法的空间复杂度为O（1）。

KMP算法   

        KMP算法的主要思想

    上述算法的时间复杂度之所以大，是由于索引指针的回溯引起的，针对以上不足，便有了KMP算法。KMP算法可以在O（Plen+Tlen）的时间数量级上完成串的模式匹配操作。其改进之处在于：每一趟比较重出现字符不等时，不需要回溯索引指针i，而是利用已经得到的部分匹配的结果将子串向右滑动尽可能远的距离，继续进行比较。它的时间复杂度为O（Plen+Tlen），空间复杂度为O（Plen），这从后面的代码中可以看出。