动态规划算法--解最长公共子序列问题

最新推荐文章于 2024-02-07 22:53:52 发布

proplume

最新推荐文章于 2024-02-07 22:53:52 发布

阅读量1w

点赞数 13

分类专栏：算法文章标签：动态规划 Python 最长公共子序列

本文链接：https://blog.csdn.net/proplume/article/details/78881529

版权

算法专栏收录该内容

2 篇文章 0 订阅

订阅专栏

如今最好，没有来日方长！

一、简述动态规划算法

1.动态规划算法简介

（1）背景

动态规划(英语：Dynamic programming，简称：DP)是一种算法设计技术，是运筹学的一个分支，是求解决策过程(Decision process)最优化的数学方法。值得注意的是，这个技术名字中的“programming”是计划和规划的意思，不是计算机领域中的编程。它有着有趣的历史。
它由20世纪50年代初美国一位卓越的数学家Richard Bellman所发明。数学家们在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题逐个求解，创立了解决这类过程优化问题的新方法——动态规划。

（2）基本思想

动态规划算法通常用于求解最优决策的问题。其基本思想是基于初始状态，将待求解问题分解成若干个子问题，其中当前子问题的解由上一次子问题的解推出，然后从这些子问题的解得到原问题的解。具体的动态规划算法有很多种，它们都用一个表来记录所有已解子问题的答案，以此避免重复计算，而节约时间。

（3）实例分析理解

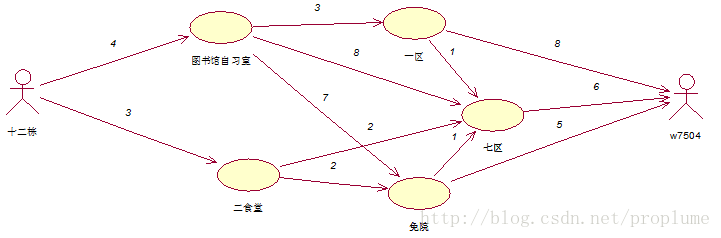
这里写图片描述

假设情景：某一天中午起床晚了，十二栋到惟义楼w7504的路
路线很多，只有走最短路线才能避免迟到。路线及所花时间，如上图所示，求解最短路线
应用动态规划算法的理解：将该过程分为A.B.C.D四阶段，每个阶段中，都求出本阶段的各个初始状态到过程终点的最短路径和最短距离，逆序倒推到起点十二栋时，便得到十二栋到教室的最短路径及最短距离。

2.算法特点

显而易见，动态规划算法可以很好的求解最优化问题。可以有效地解决冗余，降低原来具有指数级复杂度算法的时间复杂度。
最大的特点就是可以求得最优策略，符合最优化原理，即“最优策略的子策略也是最优策略”。
但是，任何思想方法都有一定的局限性。
因此，动态规划也有一些适用条件，即：适用动态规划的问题必须满足最优化原理和无后效性。简单说明，最优化原理即：一个最优化策略的子策略总是最优的；无后向性即：每个阶段的历史状态无法直接影响它的未来决策，只能通过当前的这个状态做出决策。例如，我在阶段B的某位置，阶段C“图书馆”以及“二食堂”的位置不会影响我选择哪条路。

3.动态规划算法应用

动态规划算法普遍在数学、经济学、计算机科学中使用。在最优控制、生产调度、机器学习等方面得到了广泛的应用。例如最短路线、库存管理、资源分配、设备更新、排序、背包问题、图像数据压缩、手势识别、语音识别、数据挖掘、信息检索以及最长公共子序列等应用问题。

二、问题求解

1.算法设计与论证

采用动态规划算法思想求解最长公共子序列，先将问题分解成若干个子问题，再求解子问题的最优子策略，最后求解原问题的最优策略。

（1）基本概念

在分析最长公共子序列的最优子结构前，先清楚以下概念:
子序列：某个序列的子序列指从原序列中不破坏顺序地任意除去若干个字符后形成的序列。
例：序列X，Y，其中X=“BABBCDB”，Y=“BDB”，则Y是X的一个子序列。

公共子序列：如果Z是X的子序列也是Y的子序列，那么Z是序列X与Y的公共子序列

最长公共子序列结构性质：第i前缀
如序列A=(a1,a2,…..,am)，则Ai=(a1,….,ai-1,ai)是序列A的第i前缀。
例：A=(A,B,D,C,D),A1=(A),A2=(A,B),A3=(A,B,D)

（2）最优子结构

由最长公共子序列结构性质可分析得最优子结构，现如题，假设段落一为序列A=(a1,a2,…..,am)（设长度为m）,段落二为序列T=(t1,t2,…,tn)（设长度为n），A与T的最长公共子序列为S=(s1,s2,….,sk)（设长度为k）则：
若am=tn，则sk=am=tn且Sk-1是Am-1和Tn-1的最长公共子序列；
若am≠tn且sk≠am ，则S是Am-1和T的最长公共子序列；
若am≠tn且sk≠tn ，则S是A和Tn-1的最长公共子序列
根据最长公共子序列的最优子结构可知，当am=tn时，A,T的最长公共子序列即Am-1和Tn-1的最长公共子序列加上am，当am≠tn时，A,T的最长公共子序列即Am-1和T的最长公共子序列或者A和Tn-1的最长公共子序列，则A和T的最长公共子序列为这两个最长公共子序列的最长者。
因此，求解A,T的最长公共子序列问题，均包括子问题，求解Am-1,Tn-1的最长公共子序列。

（3）最优值

由最长公共子序列的最优子结构得最长公共子序列最优值，可建立如下公式，用c[i,j]表示序列Ai和Tj的最长公共子序列的长度，则：
c[i,j] = 0, i=0或j=0
c[i,j] = c[i-1,j-1]+1, ai=tj
c[i,j] = max(c[i,j-1],c[i-1,j], ai≠tj

伪代码：

Description:The longest common sub-sequence problem . 
Init: m,d {m,d:(L1+1)(L2+1)的0矩阵}
Input: s1,s2,L1,L2
Function LCS(s1,s2)
L1=length[s1];L2=length[s2]
FOR p1=1 TO L1
FOR p2=1 TO L2
            IF  s1[p1] == s2[p2]                             
m[p1+1][p2+1] = m[p1][p2]+1  
           d[p1+1][p2+1] = 1           
        IF m[p1][p2+1] >= m[p1+1][p2]                
m[p1+1][p2+1] = m[p1][p2+1]   
            d[p1+1][p2+1] = 2           
        ELSE                                        
        m[p1+1][p2+1] = m[p1+1][p2]     
            d[p1+1][p2+1] = 3           
            ENDIF
         ENDIF
    ENDFOR 
ENDFOR 
Output: m,d

代码实现：

import numpy as np
#np.set_printoptions(threshold = 1e6)#设置打印数量阈值，避免打印省略号
def LCS(s1, s2):   
    # 序列长度加1的0矩阵
    # m用来保存对应位置匹配的结果  
    m = [ [ 0 for x in range(len(s2)+1) ] for y in range(len(s1)+1) ]   
    # d用来记录回溯矩阵 
    d = [ [ 0 for x in range(len(s2)+1) ] for y in range(len(s1)+1) ]   
    for p1 in range(len(s1)):   
        for p2 in range(len(s2)):   
            if s1[p1] == s2[p2]:              #匹配成功，取左上方的值加1，并标记回溯数字1  
                m[p1+1][p2+1] = m[p1][p2]+1  
                d[p1+1][p2+1] = 1           
            elif m[p1][p2+1] >= m[p1+1][p2]:  #左边值大于上边值，则取左值，并标记回溯数字2  
                m[p1+1][p2+1] = m[p1][p2+1]   
                d[p1+1][p2+1] = 2           
            else:                             #上值大于左值，则该位置的值为上值，并标记回溯数字3
                m[p1+1][p2+1] = m[p1+1][p2]     
                d[p1+1][p2+1] = 3         
    p1, p2 = len(s1), len(s2)
    print(m[p1][p2])
    #print(np.array(m))                        #打印对应位置匹配矩阵
    #print (np.array(d))                       #打印回溯矩阵 
    #回溯 构造最长公共子序列
    s = ''                  #存储最长公共子序列
    while m[p1][p2]:        #不为0时  
        c = d[p1][p2]
        if c == 1:          #匹配成功，插入1，并向左上角找下一个  
            s=s1[p1-1]+s
            p1-=1  
            p2-=1   
        if c ==2:           #根据标记，向左找下一个  
            p1 -= 1  
        if c == 3:          #根据标记，向上找下一个  
            p2 -= 1    
    return s

具体算法语言描述：
用矩阵记录两个基因序列的匹配程度，如果匹配则左上方的数字+1，否则取左边和上边的最大值，如果左边值大于上边值，则取左边值并标记回溯数字“3”，如果上边值大于左边值，则取上边值并标记回溯数字“2”，如果左边值等于上边值，则取上边值并标记回溯数字“2”。

测试：

if __name__ == '__main__':   

    x = 'ACAAGATGCCATTGTCC'
    y = 'TATAAATGTGTACA'
    print(LCS(x,y))

匹配矩阵：

[[ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  1  1  1  1  1  1  1  1  1  1  1  1  1]
 [ 0  0  1  1  1  1  1  1  1  1  1  1  1  2  2]
 [ 0  0  1  1  2  2  2  2  2  2  2  2  2  2  3]
 [ 0  0  1  1  2  3  3  3  3  3  3  3  3  3  3]
 [ 0  0  1  1  2  3  3  3  4  4  4  4  4  4  4]
 [ 0  0  1  1  2  3  4  4  4  4  4  4  5  5  5]
 [ 0  1  1  2  2  3  4  5  5  5  5  5  5  5  5]
 [ 0  1  1  2  2  3  4  5  6  6  6  6  6  6  6]
 [ 0  1  1  2  2  3  4  5  6  6  6  6  6  7  7]
 [ 0  1  1  2  2  3  4  5  6  6  6  6  6  7  7]
 [ 0  1  2  2  3  3  4  5  6  6  6  6  7  7  8]
 [ 0  1  2  3  3  3  4  5  6  7  7  7  7  7  8]
 [ 0  1  2  3  3  3  4  5  6  7  7  8  8  8  8]
 [ 0  1  2  3  3  3  4  5  6  7  8  8  8  8  8]
 [ 0  1  2  3  3  3  4  5  6  7  8  9  9  9  9]
 [ 0  1  2  3  3  3  4  5  6  7  8  9  9 10 10]
 [ 0  1  2  3  3  3  4  5  6  7  8  9  9 10 10]]

回溯矩阵

[[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
 [0 2 1 3 1 1 1 3 3 3 3 3 1 3 1]
 [0 2 2 2 2 2 2 2 2 2 2 2 2 1 3]
 [0 2 1 2 1 1 1 3 3 3 3 3 1 2 1]
 [0 2 1 2 1 1 1 3 3 3 3 3 1 3 1]
 [0 2 2 2 2 2 2 2 1 3 1 3 3 3 3]
 [0 2 1 2 1 1 1 3 2 2 2 2 1 3 1]
 [0 1 2 1 2 2 2 1 3 1 3 1 2 2 2]
 [0 2 2 2 2 2 2 2 1 3 1 3 3 3 3]
 [0 2 2 2 2 2 2 2 2 2 2 2 2 1 3]
 [0 2 2 2 2 2 2 2 2 2 2 2 2 1 2]
 [0 2 1 2 1 1 1 2 2 2 2 2 1 2 1]
 [0 1 2 1 2 2 2 1 2 1 3 1 2 2 2]
 [0 1 2 1 2 2 2 1 2 1 2 1 3 3 2]
 [0 2 2 2 2 2 2 2 1 2 1 2 2 2 2]
 [0 1 2 1 2 2 2 1 2 1 2 1 3 3 3]
 [0 2 2 2 2 2 2 2 2 2 2 2 2 1 3]
 [0 2 2 2 2 2 2 2 2 2 2 2 2 1 2]]

最长公共子序列及长度：

10
AAAATGTGTC

也可以用来检测文档间的匹配度，只需要增加以下内容即可：

def loadData(filename):
    import jieba
    txt = open(filename).read()
    for char in '！，。·~、？‘；“：”+-|、||《》{}【】&*（）-&……%':
        words = jieba.lcut(txt)
        words = txt.replace(char," ")     #噪声处理，将特殊字符替换为空格

    return words


if __name__ == '__main__': 
    txt1 = loadData('三生三世十里桃花.txt')
    txt2 = loadData('桃花债.txt')
    print(LCS(txt2,txt1))

三、算法复杂度分析及优化

对于一个具体的问题，设计与分析得出的算法，往往考虑两点，一即算法正确性；二即算法的时间及空间复杂度。

动态规划算法求最长公共子序列问题的时间复杂度为和空间复杂度均为：Ο(mn)

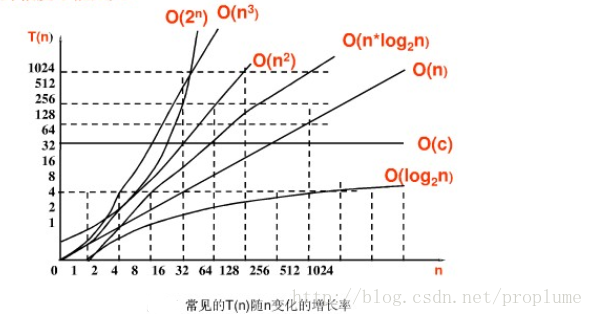
常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜O(nlog2n)＜Ο(n²)＜Ο(n³)＜…＜Ο(2ⁿ)＜Ο(n!)
则Ο(n²)＜Ο(mn)<Ο(n³)，如下图所示，当n越大所需时间随指数级增长。
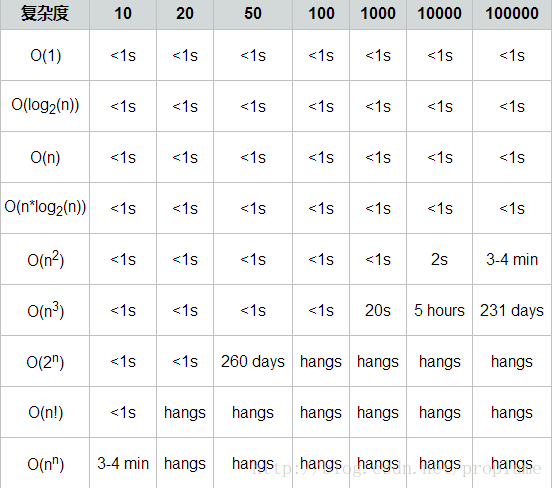
这里写图片描述

复杂度与计算时间关系如下图，虽然动态规划算法有效地降低了指数级增长的复杂度，但当数据较大时，复杂度仍旧递增增长，查资料显示可以将此问题时间复杂度降低到Ο(nlogn)，由于目前我的算法优化程度不够，所以，这里提取《三生三世十里桃花》前三章的内容以及《桃花债》前十章的内容，进行求解其最长公共子序列的长度。

这里写图片描述

去除矩阵d后优化代码如下：

import numpy as np
def LCS(s1, s2):   
    # 序列长度加1的0矩阵
    # m用来保存对应位置匹配的结果  
    m = [ [ 0 for x in range(len(s2)+1) ] for y in range(len(s1)+1) ]     
    for p1 in range(len(s1)):   
        for p2 in range(len(s2)):   
            if s1[p1] == s2[p2]:              #匹配成功，取左上方的值加1  
                m[p1+1][p2+1] = m[p1][p2]+1             
            else:                             #取左边值和上边值的大值
                m[p1+1][p2+1] = max(m[p1+1][p2], m[p1][p2+1])    
    p1, p2 = len(s1), len(s2)
    return m[p1][p2]

def loadData(filename):
    import jieba
    txt = open(filename).read()
    words = jieba.lcut(txt) #读取中文字符
    return words


if __name__ == '__main__': 
    txt1 = loadData('三生三世十里桃花.txt')
    txt2 = loadData('桃花债.txt')
    print(LCS(txt2,txt1))

四、总结

该算法还可以进一步优化，如果算法没有进一步优化到对数级别上，最好不要尝试100000的数据，会死机的……

proplume

关注

13
点赞
踩
44

收藏

觉得还不错? 一键收藏
0
评论
动态规划算法--解最长公共子序列问题

如今最好，没有来日方长！一、简述动态规划算法1.动态规划算法简介（1）背景动态规划(英语：Dynamic programming，简称：DP)是一种算法设计技术，是运筹学的一个分支，是求解决策过程(Decision process)最优化的数学方法。值得注意的是，这个技术名字中的“programming”是计划和规划的意思，不是计算机领域中的编程。它有着有趣的历史。它由20世纪50年代初美国一
复制链接

扫一扫