快速排序, 是最经典的排序算法之一。快速排序拥有良好的时间复杂度,平均为 O(nlog2n) ,最差为 O(n2) 。在这里,我们不妨略略深入讨论一下快速排序:
时间复杂度分析
首先说平均时间复杂度。以比较常用的从两头进行扫描的算法为例,算法主要分两步:
1. 是快排的核心:“分趟”。就是“每一趟”下来,找到某一个元素应该待的位置,这个元素一般被称为pivot;
2.再分别对pivot前后两部分进行递归排序。
#include <iostream>
using namespace std;
int partition(int *a, int left, int right)
{
int key = a[left];
while(left < right){
while(left < right && a[right] >= key) right--; //从右找到第一个比key小的
a[left] = a[right];
while(left < right && a[left] <= key) left++; //从左找到第一个比key大的
a[right] = a[left];
}
a[left] = key; //基准归位
return left;
}
void Qsort(int *a, int left, int right)
{
if(left < right){ //元素长度>1时
int pos = partition(a, left, right);
Qsort(a, left, pos - 1); //pos本身不需要再动了
Qsort(a, pos + 1, right);
}
}
int main()
{
int a[] = {57, 68, 59, 52, 72, 28, 96, 33, 24};
Qsort(a, 0, sizeof(a) / sizeof(a[0]) - 1);
for(int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
cout << a[i] << " ";
}
return 0;
}显然,一趟下来,pivot被固定的位置越趋于中间,前后两部分子序列的递归调用就越均衡,这时候时间复杂度是最小的。
T(n) <= n + 2T(n/2)
<= 2n + 4T(n/4)
<= 3n + 8T(n/8)
...
<= (log n)n + nT(1) = O(nlog n)因此,为 O(nlog2n) 。
最差的情况下,也就是pivot被固定后的位置总是在最前面或最后面,导致前后两部分子序列实际只是一个子序列。这也就意味着,原代排序列本身就是有序的,要么从小到大,要么从大到小。比如从小到大:此时,第一趟经过n-1次比较,将第一个元素固定在首位;第二趟经过n-2次比较,将第二个元素固定在第二位,以此类推,n个元素总共要比较 1+2+3+...+(n−1)=n(n−1)/2 次,所以复杂度为 O(n2) 。当然,如果从简单形象的角度去理解,一般的快排执行过程大概是二叉树形结构,而最差情况则是退化成了链表。
优化
优化大致有三种比较有效的方法。
使用插入排序
在子序列比较小的时候,其实插排是比较快的,因为对于有序的序列,插排可以达到 O(n) 的复杂度,如果序列比较小,则和大序列比起来会更加有序,这时候使用插排效率要比快排高。其实现方法也很简单:快排是在子序列元素个数变成1是,才停止递归,我们可以设置一个阈值n,假设为5,则大于5个元素,子序列继续递归,否则选用插排。(其实在C++的STL中,归并算法就是采用了这个思路,当子序列小到一定程度的时候,直接选用插排对子序列进行排序)
快排是在待排数列越趋近于有序时变得越慢,复杂度越高,调用插排可以很好的解决这个问题。
pivot选用中位数
对于一般的快排,我们直接简单的就取最左或最右的数据作为pivot,这样的话很可能遇到比较极端的pivot,使得划分出来的左右子序列变得不均衡。如果选取最左、中间、最右这三个值的中位数的话,显然会使得pivot更加“不偏激”,这样划分出来的左右子序列也会更加均衡。
选用中位数和调用插排一样,都能避免数列比较有序时复杂度变高的问题。
三路划分
快排是二路划分的算法。如果待排序列中重复元素过多,也会大大影响排序的性能。这时候,如果采用三路划分,则会很好的避免这个问题。
如果一个带排序列重复元素过多,我们先随机选取一个pivot,设为T,那么数列可以分为三部分:小于T,等于T,大于T:

等于T的部分就无需再参与后续的递归调用了,速度自然就大大提升了。
但是问题在于怎么高效地将序列划分为三部分!
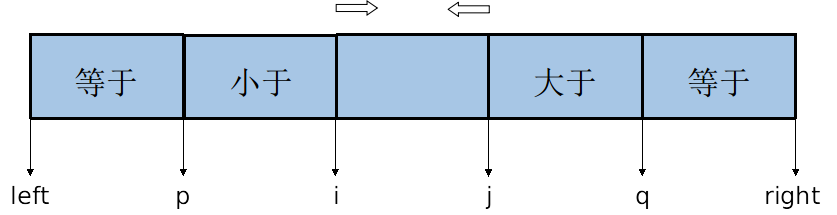
如下图,我们可以设置四个游标,左端a、b,右端c、d。b、c的作用跟之前两路划分时候的左右游标相同,就是从两端向中间遍历序列,并将遍历到的元素与pivot比较,如果等于pivot,则移到两端(b对应的元素移到左端,c对应的元素移到右端。移动的方式就是拿此元素和a或d对应的元素进行交换,所以a和d的作用就是记录等于pivot的元素移动过后的边界),反之,如果大于或小于pivot,还按照之前两路划分的方式进行移动。这样一来,中间部分就和两路划分相同,两头是等于pivot的部分,我们只需要将这两部分移动到中间即可。


参考算法如下,摘自http://blog.csdn.net/jlqCloud/article/details/46939703:
private void quickSort(int[] a, int left, int right) {
if (right <= left)
return;
/*
* 工作指针
* p指向序列左边等于pivot元素的位置
* q指向序列右边等于Pivot元素的位置
* i指向从左向右扫面时的元素
* j指向从右向左扫描时的元素
*/
int p, q, i, j;
int pivot;// 锚点
i = p = left;
j = q = right - 1;
/*
* 每次总是取序列最右边的元素为锚点
*/
pivot = a[right];
while (true) {
/*
* 工作指针i从右向左不断扫描,找小于或者等于锚点元素的元素
*/
while (i < right && a[i] <= pivot) {
/*
* 找到与锚点元素相等的元素将其交换到p所指示的位置
*/
if (a[i] == pivot) {
swap(a, i, p);
p++;
}
i++;
}
/*
* 工作指针j从左向右不断扫描,找大于或者等于锚点元素的元素
*/
while (left <= j && a[j] >= pivot) {
/*
* 找到与锚点元素相等的元素将其交换到q所指示的位置
*/
if (a[j] == pivot) {
swap(a, j, q);
q--;
}
j--;
}
/*
* 如果两个工作指针i j相遇则一趟遍历结束
*/
if (i >= j)
break;
/*
* 将左边大于pivot的元素与右边小于pivot元素进行交换
*/
swap(a, i, j);
i++;
j--;
}
/*
* 因为工作指针i指向的是当前需要处理元素的下一个元素
* 故而需要退回到当前元素的实际位置,然后将等于pivot元素交换到序列中间
*/
i--;
p--;
while (p >= left) {
swap(a, i, p);
i--;
p--;
}
/*
* 因为工作指针j指向的是当前需要处理元素的上一个元素
* 故而需要退回到当前元素的实际位置,然后将等于pivot元素交换到序列中间
*/
j++;
q++;
while (q <= right) {
swap(a, j, q);
j++;
q++;
}
/*
* 递归遍历左右子序列
*/
quickSort(a, left, i);
quickSort(a, j, right);
}
private void quick(int[] a) {
if (a.length > 0) {
quickSort(a, 0, a.length - 1);
}
}
private void swap(int[] arr, int a, int b) {
int temp = arr[a];
arr[a] = arr[b];
arr[b] = temp;
}三路划分可以避免很多重复元素再次参与递归,对于有大量重复元素的待排序列,效率提高了不少。
以上只是理论上的总结,当然实践起来代码也不难写。在这里推荐一篇有码有实验数据的文章,看后也是更加直观形象,受益匪浅。
快排的优化其实对于一个计算机科学与技术的入门者来讲,是一个不错的思维上的砥砺,这种类型的东西多多探索,计算机科学“素养”自然慢慢就上去了。






















 8451
8451

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








