前言:
红黑树是一棵二叉搜索树,它在每个节点上增加了一个存储位来表示节点的颜色,可以是Red或Black。通过对任何一条从根到叶子简单路径上的颜色来约束,红黑树保证最长路径不超过最短路径的两倍,因而近似于平衡。
红黑树的基本概念:
红黑树是满足下面红黑性质的二叉搜索树
1. 每个节点,不是红色就是黑色的
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个子节点是黑色的(不能有连续的两个红节点)
4. 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
5. 每个叶子节点都是黑色的(这里的叶子节点是指的NIL节点(空节点))
红黑树的插入写法要根据红黑树插入的各种情况来分析:
ps:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
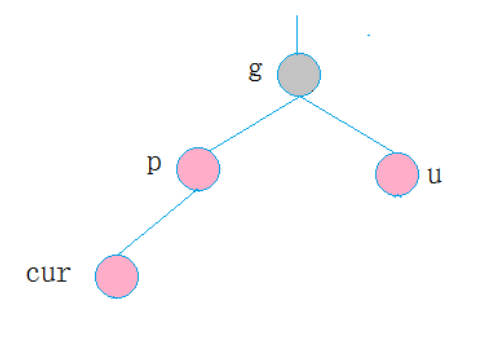
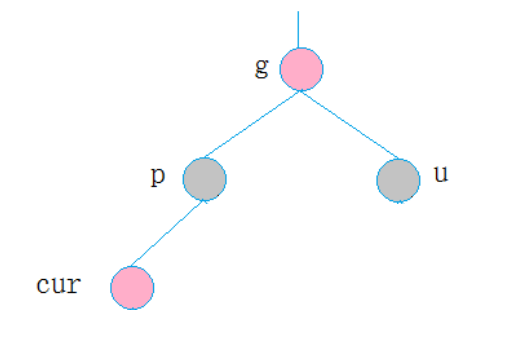
1.第一种情况
cur为红,p为红,g为黑,u存在且为红
则将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
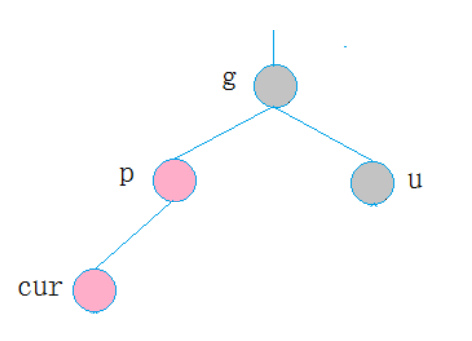
2.第二种情况
cur为红,p为红,g为黑,u不存在/u为黑
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色--p变黑,g变红
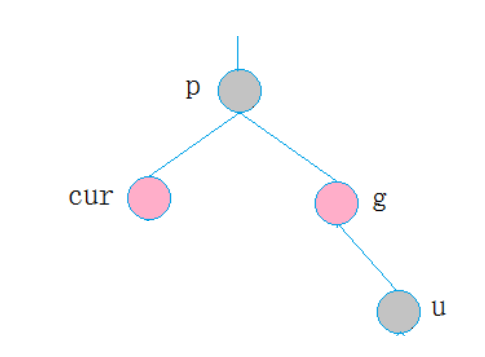
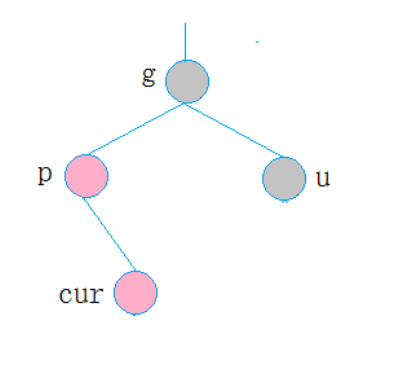
3.第三种情况
cur为红,p为红,g为黑,u不存在/u为黑
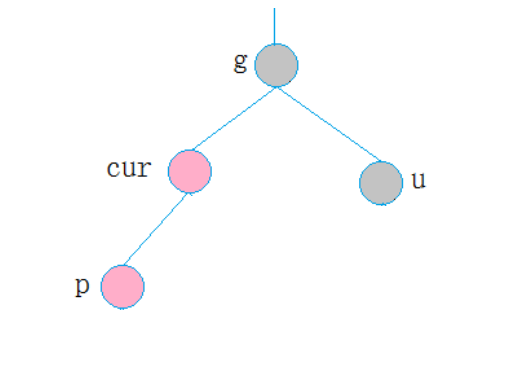
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
则转换成了情况2
上面已经把没种情况列出来了,其他相反的情况类似,反过来写一下就行了,具体细节过程见代码,
- #ifndef __RBTREE_H__
- #define __RBTREE_H__
- enum colour
- {
- RED,
- BLACK,
- };
- template<class K,class V>
- struct RBTreeNode
- {
- int _col;
- K _key;
- V _value;
- RBTreeNode<K, V>* _left;
- RBTreeNode<K, V>* _right;
- RBTreeNode<K, V>* _parent;
- RBTreeNode(const K& key, const V& value)
- :_key(key)
- , _value(value)
- , _col(RED)
- , _left(NULL)
- , _right(NULL)
- , _parent(NULL)
- {}
- };
- template<class K,class V>
- class RBTree
- {
- typedef RBTreeNode<K, V> Node;
- public:
- RBTree()
- :_root(NULL)
- {}
- bool Insert(const K& key, const V& value)
- {
- if (_root == NULL)
- {
- _root = new Node(key, value);
- _root->_col = BLACK;
- return true;
- }
- Node* parent = NULL;
- Node* cur = _root;
- while (cur)
- {
- if (cur->_key > key)
- {
- parent = cur;
- cur = cur->_left;
- }
- else if (cur->_key < key)
- {
- parent = cur;
- cur = cur->_right;
- }
- else
- return false;
- }
- //插入位置
- if (parent->_key >key)
- {
- cur = new Node(key, value);
- parent->_left = cur;
- cur->_parent = parent;
- }
- else if (parent->_key < key)
- {
- cur = new Node(key, value);
- parent->_right = cur;
- cur->_parent = parent;
- }
- //插入位置以后,如何调整
- while (cur != _root && parent->_col == RED)
- {
- Node* grandfather = parent->_parent;
- Node* uncle = NULL;
- //左边的情况
- if (parent == grandfather->_left)
- {
- //情况一
- uncle = grandfather->_right;
- if (uncle && uncle->_col == RED)
- {
- //情况1-> 不需要旋转
- if (cur == parent->_left)
- {
- grandfather->_col = RED;
- parent->_col = BLACK;
- uncle->_col = BLACK;
- cur = grandfather;
- parent = cur->_parent;
- }
- //需要旋转
- else if (cur == parent->_right)
- {
- RotateL(parent);
- grandfather->_col = RED;
- parent->_col = BLACK;
- uncle->_col = BLACK;
- cur = grandfather;
- parent = cur->_parent;
- }
- }
- //情况2,情况3
- else if (uncle == NULL || (uncle && uncle->_col == BLACK))
- {
- //情况3
- if (cur == parent->_right)
- {
- RotateL(parent);
- }
- parent->_col = BLACK;
- grandfather->_col = RED;
- RotateR(grandfather);
- break;
- }
- }
- //右边的情况
- else if (parent == grandfather->_right)
- {
- //情况1
- uncle = grandfather->_left;
- if (uncle && uncle->_col == RED)
- {
- //不需要旋转
- if (cur == parent->_right)
- {
- uncle->_col = BLACK;
- grandfather->_col = RED;
- parent->_col = BLACK;
- cur = grandfather;
- parent = cur->_parent;
- }
- //旋转
- else if (cur == parent->_left)
- {
- uncle->_col = BLACK;
- grandfather->_col = RED;
- parent->_col = BLACK;
- RotateR(parent);
- cur = grandfather;
- parent = cur->_parent;
- }
- }
- else if (uncle == NULL || (uncle && uncle->_col == BLACK))
- {
- //情况2,3
- if (cur == parent->_left)
- {
- RotateR(parent);
- }
- parent->_col = BLACK;
- grandfather->_col = RED;
- RotateL(grandfather);
- break;
- }
- }
- }
- _root->_col = BLACK;
- return true;
- }
- bool isRBTree()
- {
- int blackNodeNum = 0;
- int curBlackNodeNum = 0;
- Node* cur = _root;
- while (cur)
- {
- if (cur->_col == BLACK)
- blackNodeNum++;
- cur = cur->_left;
- }
- return _isRBTree(_root,blackNodeNum,curBlackNodeNum);
- }
- void InOrder()
- {
- _InOrder(_root);
- }
- protected:
- bool _isRBTree(Node* root,int blackNodeNum,int curBlackNodeNum)
- {
- if (root == NULL)
- return true;
- if (root->_col == BLACK)
- curBlackNodeNum++;
- if (blackNodeNum == curBlackNodeNum)
- {
- if (root->_parent == NULL)
- return true;
- else if (root->_col == RED && root->_col == root->_parent->_col)
- {
- return false;
- }
- else
- {
- return true;
- }
- }
- return _isRBTree(root->_left, blackNodeNum, curBlackNodeNum) && _isRBTree(root->_right, blackNodeNum, curBlackNodeNum);
- }
- void _InOrder(Node* root)
- {
- if (root == NULL)
- return;
- _InOrder(root->_left);
- cout << root->_key << " ";
- _InOrder(root->_right);
- }
- void RotateL(Node*& parent)
- {
- Node* subR = parent->_right;
- Node* subRL = subR->_left;
- parent->_right = subRL;
- if (subRL)
- subRL->_parent = parent;
- subR->_left = parent;
- subR->_parent = parent->_parent;
- parent->_parent = subR;
- parent = subR;
- if (parent->_parent == NULL)
- _root = parent;
- else if (parent->_parent->_key > parent->_key)
- {
- parent->_parent->_left = parent;
- }
- else if (parent->_key > parent->_parent->_key)
- {
- parent->_parent->_right = parent;
- }
- }
- void RotateR(Node*& parent)
- {
- Node* subL = parent->_left;
- Node* subLR = subL->_right;
- parent->_left = subLR;
- if (subLR)
- subLR->_parent = parent;
- subL->_right = parent;
- subL->_parent = parent->_parent;
- parent->_parent = subL;
- parent = subL;
- if (parent->_parent == NULL)
- _root = parent;
- else if (parent->_parent->_key > parent->_key)
- {
- parent->_parent->_left = parent;
- }
- else if (parent->_parent->_key < parent->_key)
- parent->_parent->_right = parent;
- }
- protected:
- Node* _root;
- };
- void testRBtree()
- {
- RBTree<int, int> rbt;
- int arr[8] = { 2, 5, 12, 16, 18, 26, 3, 1 };
- for (int i = 0; i < 8; i++)
- {
- rbt.Insert(arr[i], i);
- }
- rbt.InOrder();
- cout << endl;
- cout << "isRBTree? ->:" << rbt.isRBTree() << endl;
- }
- #endif //__RBTREE_H__






















 170万+
170万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








