排序算法JAVA实现二

时间复杂度为 O（n*log（n））的算法：归并排序、快速排序、堆排序、希尔排序

题： 对于一个int数组，请编写一个排序算法，对数组元素排序。
给定一个int数组A及数组的大小n，请返回排序后的数组。
测试样例：
　　[1,2,3,5,2,3],6
　　[1,2,2,3,3,5]

一，归并排序

　　归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
　　
　　归并过程为：比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素a[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]

归并操作的工作原理如下：
　　第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
　　第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置
　　第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
　　第四步：重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾

JAVA代码实现：

package Sort;
import java.util.*;
public class MergeSort {
     public int[] mergeSort(int[] A, int n ) {
            process(A,0,n-1);   
            return A;
        }  

     void process(int[] A,int l,int r){
            int mid=(l+r)/2;
            if(l < r) {  
              process(A,l,mid);
              process(A,mid+1,r);   
              merge(A,l,mid,r);              
            }
        }  

     void merge(int[] nums,int low,int mid, int high ){
           int[] temp = new int[high - low + 1];  
           int i = low;// 左指针  
           int j = mid + 1;// 右指针  
           int k = 0;    
           // 把较小的数先移到新数组中  
           while (i <= mid && j <= high) {  
               if (nums[i] < nums[j]) {  
                   temp[k++] = nums[i++];  
               } else {  
                   temp[k++] = nums[j++];  
               }  
           }   
          // 把左边剩余的数移入数组  
          while (i <= mid) {  
              temp[k++] = nums[i++];  
           }  
         // 把右边边剩余的数移入数组  
          while (j <= high) {  
             temp[k++] = nums[j++];  
         }  
         // 把新数组中的数覆盖nums数组  
         for (int k2 = 0; k2 < temp.length; k2++) {  
           nums[k2 + low] = temp[k2];  
          }  
       }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] A = { 1, 2,  3, 5, 2, 6};  
        int n=6;
        MergeSort ms = new MergeSort();
        ms.mergeSort(A, n);  
        System.out.println(Arrays.toString(A)); 
    }

}

二，快速排序

　　快速排序（Quicksort）是对冒泡排序的一种改进。
　　快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

一趟快速排序的算法是：
　1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；
　2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；
　3）从j开始向前搜索，即由后开始向前搜索(j–)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；
　4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；
　5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）。

JAVA实现：

package Sort;
import java.util.*;
public class QuickSort {
    public int[] quickSort(int[] A, int n) {
        // write code here
        if (A == null || n == 0) return null;
        Sort(A,0,n-1);
        return A;
    }

    void Sort(int[] A,int left,int right){
        if(left<right){
            int q=Partition(A,left,right);
            Sort(A,left,q-1);
            Sort(A,q+1,right);
        }
    }

    int Partition(int[] A,int left,int right){          
           int key = A[left];  
           while (left < right) { 
               //由后开始向前搜索，找到第一个小于key的值A[right]
               while (left < right && A[right] >= key) --right;  
               //交换
               A[left] = A[right];  
               while (left < right &&  A[left] <= key) ++left;  
               A[right] = A[left];  
           }   
           A[left] = key;     
           return left; 
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
            int[] A = { 1, 2,  3, 5, 2, 6};  
            int n=6;
            QuickSort qs = new QuickSort();
            qs.quickSort(A, n);  
            System.out.println(Arrays.toString(A)); 
    }
}

三，堆排序

　　堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆，是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值，即A[PARENT[i]] >= A[i]。在数组的非降序排序中，需要使用的就是大根堆，因为根据大根堆的要求可知，最大的值一定在堆顶。
　　

　
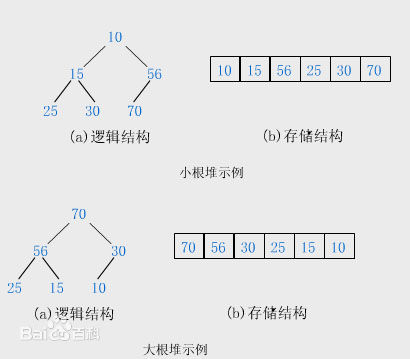
　用大根堆排序的基本思想
　　① 先将初始文件R[1..n]建成一个大根堆，此堆为初始的无序区
　　② 再将关键字最大的记录R[1]（即堆顶）和无序区的最后一个记录R[n]交换，由此得到新的无序区R[1..n-1]和有序区R[n]，且满足R[1..n-1].keys≤R[n].key
　　③由于交换后新的根R[1]可能违反堆性质，故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换，由此得到新的无序区R[1..n-2]和有序区R[n-1..n]，且仍满足关系R[1..n-2].keys≤R[n-1..n].keys，同样要将R[1..n-2]调整为堆。
……
直到无序区只有一个元素为止

JAVA实现：

package Sort;
import java.util.Arrays;

public class HeapSort {
        public int[] heapSort(int[] A, int n) {
            // write code here
            if(n < 2) return A;          
            for(int i = 0; i < n; i++) {      
                adjust(A, 0, n - i);               
                swap(A, 0, n - 1 - i);        
            }                  
            return A;
        }  

        void adjust(int[] A, int root, int size) { 
            if(root*2 + 1 < size) {      
                adjust(A, root * 2 + 1, size);       
                }         
            if(root * 2 + 2 < size) {      
                adjust(A, root * 2 + 2, size);    
                }         
            int MAX = root;   
            if(root * 2 + 1 < size) {      
                if(A[root * 2 + 1] > A[root]) {         
                    MAX = root * 2 + 1;            
                    }        
            }         
            if(root * 2 + 2 < size) {      
                if(A[root * 2 + 2] > A[MAX]) {         
                    MAX = root * 2 + 2;           
                    }       
                }        
                swap(A, root, MAX);   
            }   

        void swap(int[] A, int a, int b) {  
            if(a == b) return;            
            int temp = A[a];   
            A[a] = A[b];    
            A[b] = temp;   
            }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] A = { 1, 2,  3, 5, 2, 6};  
        int n=6;
        HeapSort hs = new HeapSort();
        hs.heapSort(A, n);  
        System.out.println(Arrays.toString(A));
    }
}

四，希尔排序

　　希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因DL．Shell于1959年提出而得名。
　　希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

　　希尔排序是基于插入排序的以下两点性质而提出改进方法的：插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。

　该方法实质上是一种分组插入方法：
　　相隔较远距离（称为增量）的数，使得数移动时能跨过多个元素，则进行一次比[2] 较就可能消除多个元素交换。D.L.shell于1959年在以他名字命名的排序算法中实现了这一思想。算法先将要排序的一组数按某个增量d分成若干组，每组中记录的下标相差d.对每组中全部元素进行排序，然后再用一个较小的增量对它进行，在每组中再进行排序。当增量减到1时，整个要排序的数被分成一组，排序完成。
　　一般的初次取序列的一半为增量，以后每次减半，直到增量为1。

JAVA实现：

package Sort;
import java.util.Arrays;

public class ShellSort {
    public int[] shellSort(int[] A, int n) {
        // write code here
        for(int gap = n/2 ;
            gap >= 1; gap /= 2){      
            for(int i = gap; i < n; i++){         
                for(int j = i - gap ; j >= 0 ; j -= gap){           
                    if(A[j] > A[j + gap]){                
                        int temp = A[j];                 
                        A[j] = A[j + gap];                
                        A[j + gap] = temp;            
                    }           
                }      
            }
        }
        return A;
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] A = { 1, 2,  3, 5, 2, 6};  
        int n=6;
        ShellSort ss = new ShellSort();
        ss.shellSort(A, n);  
        System.out.println(Arrays.toString(A));
    }

}