最短路径算法（上）——迪杰斯特拉（Dijikstra）算法

最新推荐文章于 2022-08-10 13:45:00 发布

daipuweiai

最新推荐文章于 2022-08-10 13:45:00 发布

阅读量8.9k

点赞数 8

分类专栏： # 数据结构数据结构与算法专栏文章标签：数据结构图迪杰斯特拉 Dijikstra

本文链接：https://blog.csdn.net/qq_30091945/article/details/77949979

版权

数据结构同时被 2 个专栏收录

100 篇文章 11 订阅

订阅专栏

数据结构与算法专栏

56 篇文章 21 订阅

订阅专栏

前记

对于迪杰斯特拉算法的分支界限法解法请移步：利用分支界限法求解Dijikstra算法

概述

单源最短路径问题，即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前，必须弄清楚最短路径的最优子结构性质。

最短路径的最优子结构性质描述为：如果P(i,j)={Vi…Vk…Vs…Vj}是从顶点i到j的最短路径，k和s是这条路径上的一个中间顶点，那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。

假设P(i,j)={Vi…Vk…Vs…Vj}是从顶点i到j的最短路径，则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离，那么必定存在另一条从k到s的最短路径P’(k,s)，那么P’(i,j)=P(i,k)+P’(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。

无权图的最短路径算法

对于无权图来说，可以把它当作每条边都为1的有权图。故无权图的最短路径算法如下：
1）初始化距离数组dist和路径数组path全为-1，同时定义一个队列queue，初始化队列为空。
2）把源点vertex入队并更新dist[vertex]=0
3）当队列不空是一直循环，利用cur_vertex保存出队元素，遍历cur_vertex的每个邻接点i，若dist[i] =-1，那么将其入队，更新dist[i] = dist[cur_vertex]+1,path[i] = cur_vertex。
算法如下：

//无权图的Dijikstra
void Unweighted(int vertex){
	queue<int> queue;		//初始化队列
	queue.push(vertex);		//初始结点入队
	int cur_vertex;			//当前结点 
	this->dist[vertex] = 0;	//初始结点的距离为0 
	while(!queue.empty()){
		cur_vertex = queue.front();	//队头结点出队 
		queue.pop();
		//遍历cur_vertex的每个邻接点 
		for(int i = 1  ; i < this->Nv+1 ; i++){
			if((this->G[cur_vertex][i] == 1)&& (this->dist[i] == -1)){
			//当前结点的距离是cur_vertex的距离加1 
				this->dist[i] = this->dist[cur_vertex]+1;
			//把当前结点的上一个结点设为cur_vertex;
				this->path[i] = cur_vertex;	
				queue.push(i); 
			}
		}
	}
}

Dijikstra算法

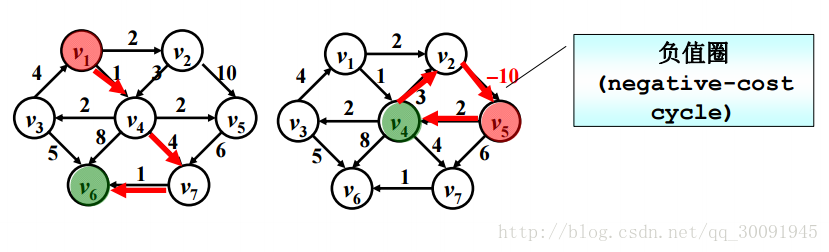
Dijikstra算法主要是针对有权图的最短路径问题提出的，且具体问题中不能出现权值为负的边，即负值圈问题，如下图所示：
这里写图片描述
对于Dijikstra算法的理解，首先得从最短路径的最优子结构说起。（这部分引用海子的博客园的Dijkstra算法（单源最短路径）一文的说法）

最短路径的最优子结构性质
该性质描述为：如果P(i,j)={Vi…Vk…Vs…Vj}是从顶点i到j的最短路径，k和s是这条路径上的一个中间顶点，那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。

假设P(i,j)={Vi…Vk…Vs…Vj}是从顶点i到j的最短路径，则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离，那么必定存在另一条从k到s的最短路径P(k,s)，那么P(i,j)=P(i,k)+P(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。

那么Dijikstra算法描述如下：
假设存在G=<V,E>，源顶点为V0，U={V0},dist[i]记录V0到i的最短距离，path[i]记录从V0到i路径上的i前面的一个顶点。
1）从V-U中选择使dist[i]值最小的顶点i，将i加入到U中；
2）更新与i直接相邻顶点的dist值。dist[j]=min{dist[j],dist[i]+matrix[i][j]}
3）直到U=V，算法停止。
起始Dijikstra算法的本质就是贪心算法。

//有权图的Dijikstra(遍历整个数组寻找最小路径顶点)
bool Dijikstra(int vertex){
	//根据初始结点初始化距离数组与路径数组 
	for(int i = 0 ; i < this->Nv+1 ; i++){
		//在构造函数里dist已经全部初始化为MAX
		//G存在边时为权重，没有边时为MAX 
		this->dist[i] = this->G[vertex][i];
		if(this->dist[i] < MAX){
			this->path[i] = vertex;
		}
	}
	this->dist[vertex] = 0;		//初始结点的距离为０
	this->collected[vertex] = 1;	//初始结点标记为已收录 
	while(1){
		//V是未被收录定点中dist最小者 
		int V = this->FindMinVertex(); 
		if(V == -1){//未找到这样的V则跳出循环 
			break;
		} 
		this->collected[V] = 1;//标记为已经被收录 
		//遍历图中每个顶点 
		for(int w = 1 ; w < this->Nv+1 ; w++){
			//若w是V的邻接点且未被收录 
			if(this->collected[w] == 0 && this->G[V][w] < MAX){
				if(this->G[V][w] < 0){//存在负边时 
					return false;	//结束算法 
				}
				//若收录V使得dist[w]变小 
				if(this->dist[V] + this->G[V][w] < this->dist[w]){
					//更新dist[w] 
					this->dist[w] = this->dist[V] = this->G[V][w]; 
					this->path[w] = V;//更新路径 
				} 
			} 
		} 
	}
	return true;
}

例子

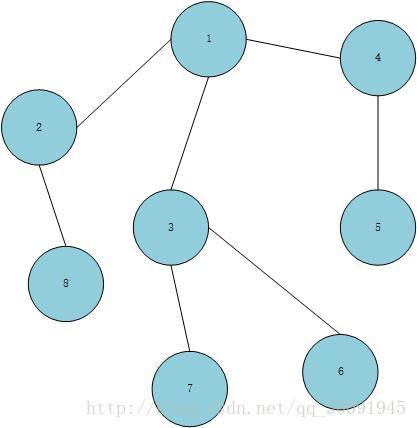
对于无权图的最小路径我们基于如下的图模型：
这里写图片描述
全部代码：

#include <iostream>
#include <cstring>
#include <queue>
#include <stack>
using namespace std;

class Graph{
	private:
		int** G;	 			//邻接矩阵 
		int* dist;				//距离数组
		int* path;				//路径数组 
		int Nv;					//顶点数
		int Ne;					//边数 
	public:
		//构造函数 
		Graph(int nv , int ne){
			this->Nv = nv;
			this->Ne = ne;
			this->G = new int*[nv+1];
			this->dist = new int[nv+1];
			this->path = new int[nv+1];
			memset(this->dist,-1,sizeof(this->dist[0])*(nv+1));
			memset(this->path,-1,sizeof(this->path[0])*(nv+1));
			for(int i = 0 ; i < nv+1 ; i++){
				G[i] = new int[nv+1];
				memset(G[i],0,sizeof(G[i][0])*(nv+1));
			}
			cout<<"请输入边："<<endl;
			for(int i = 0 ; i < ne ; i++){
				int a,b;
				cin>>a>>b;
				this->G[a][b] = 1;
				this->G[b][a] = 1;
			}
		}
		
		//无权图的Dijikstra
		void Unweighted(int vertex){
			queue<int> queue;		//初始化队列
			queue.push(vertex);		//初始结点入队
			int cur_vertex;			//当前结点 
			this->dist[vertex] = 0;		//初始结点的距离为0 
			while(!queue.empty()){
				cur_vertex = queue.front();	//队头结点出队 
				queue.pop();
				//遍历cur_vertex的每个邻接点 
				for(int i = 1  ; i < this->Nv+1 ; i++){
					if((this->G[cur_vertex][i] == 1)&& (this->dist[i] == -1)){
						this->dist[i] = this->dist[cur_vertex]+1;//当前结点的距离是cur_vertex的距离加1 
						this->path[i] = cur_vertex;	//把当前结点的上一个结点设为cur_vertex;
						queue.push(i); 
					}
				}
			}
		}
		
		//打印无权图迪杰斯特拉路径
		void Print_Unweighted(int vertex){
			for(int i = 1 ; i < this->Nv+1 ; i++){
				stack<int> stack;
				stack.push(i);
				cout<<vertex<<"到"<<i<<"的最短路径为：";
				int j = i;
				while(this->path[j] != -1){//路径上的元素一次入栈 
					j = this->path[j];
					stack.push(j);	
				}
				//打印路径 
				cout<<stack.top();
				stack.pop(); 
				while(!stack.empty()){
					cout<<" -> "<<stack.top();
					stack.pop();
				}
				cout<<endl;
			}
		}
};

int main() 
{
	cout<<"请输入顶点数与边数："<<endl; 
	int nv ,ne;
	cin>>nv>>ne;
	Graph graph(nv,ne);
	cout<<"请输入一个起始点："<<endl;
	int vertex;
	cin>>vertex;
	graph.Unweighted(vertex);
	graph.Print_Unweighted(vertex); 
	
	return 0;
}

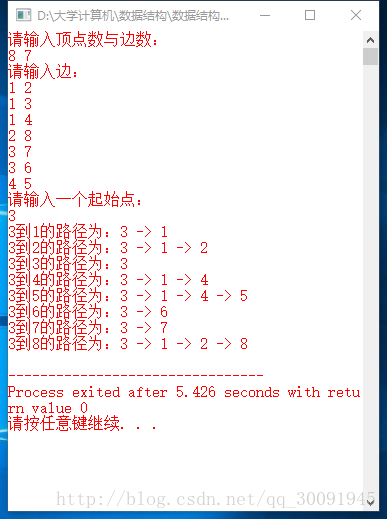
截图：
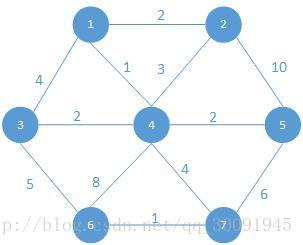
这里写图片描述

对于有权图的最短路径算法（Dijikstra）我们基于如下图模型：
这里写图片描述
全部代码：

#include <iostream>
#include <cstring>
#include <stack>
#include <stdio.h>
using namespace std;

const int MAX = 65535;

class Graph{
	private:
		int** G;	 			//邻接矩阵 
		int* dist;				//距离数组
		int* path;				//路径数组
		int* collected;			//收录数组 
		int Nv;					//顶点数
		int Ne;					//边数 
	public:
		//构造函数 
		Graph(int nv , int ne){
			this->Nv = nv;
			this->Ne = ne;
			this->G = new int*[nv+1];
			this->dist = new int[nv+1];
			this->path = new int[nv+1];
			this->collected = new int[nv+1]; 
			for(int i = 0 ; i < this->Nv+1 ; i++){
				this->dist[i] = MAX;
			}
			memset(this->path,-1,sizeof(this->path[0])*(nv+1));
			memset(this->collected,0,sizeof(this->collected[0])*(nv+1));
			for(int i = 0 ; i < nv+1 ; i++){
				this->G[i] = new int[nv+1];
				for(int j = 0 ; j < nv+1 ; j++){
					this->G[i][j] = MAX; 
				}
			}
			cout<<"请输入边与权重："<<endl;
			for(int i = 0 ; i < ne ; i++){
				int v1,v2,weight;
				cin>>v1>>v2>>weight;
				this->G[v1][v2] = weight;
				this->G[v2][v1] = weight;
			}
		}
		
		//遍历邻接点寻找最小距离顶点
		int FindMinVertex(){
			int MinDist = MAX;	//初始化最小距离
			int v,MinV = 0;
			for(v = 1 ; v < this->Nv+1 ; v++){
				if(this->collected[v] == 0 && this->dist[v] < MinDist){
					//v没有被收录且dist[v]更小
					MinDist = dist[v];
					MinV = v; 
				}
			}
			if(MinDist < MAX){//找到最小的dist 
				return MinV;	//返回对应顶点的下标 
			}else{
				return -1;	//若这样的顶点不存在则返回-1 
			} 
		} 
		
		//有权图的Dijikstra(遍历整个数组寻找最小路径顶点)
		bool Dijikstra(int vertex){
			//根据初始结点初始化距离数组与路径数组 
			for(int i = 0 ; i < this->Nv+1 ; i++){
				//在构造函数里dist已经全部初始化为MAX
				//G存在边时为权重，没有边时为MAX 
				this->dist[i] = this->G[vertex][i];
				if(this->dist[i] < MAX){
					this->path[i] = vertex;
				}
			}
			this->dist[vertex] = 0;		//初始结点的距离为０
			this->collected[vertex] = 1;	//初始结点标记为已收录 
			while(1){
				//V是未被收录定点中dist最小者 
				int V = this->FindMinVertex(); 
				if(V == -1){//未找到这样的V则跳出循环 
					break;
				} 
				this->collected[V] = 1;//标记为已经被收录 
				//遍历图中每个顶点 
				for(int w = 1 ; w < this->Nv+1 ; w++){
					//若w是V的邻接点且未被收录 
					if(this->collected[w] == 0 && this->G[V][w] < MAX){
						if(this->G[V][w] < 0){//存在负边时 
							return false;	//结束算法 
						}
						//若收录V使得dist[w]变小 
						if(this->dist[V] + this->G[V][w] < this->dist[w]){
							//更新dist[w] 
							this->dist[w] = this->dist[V] + this->G[V][w]; 
							this->path[w] = V;//更新路径 
						} 
					} 
				} 
			}
			return true;
		}
		
		//打印迪杰斯特拉路径
		void Print_Dijikstra(int vertex){
			for(int i = 1 ; i < this->Nv+1 ; i++){
				if(i == vertex){
					continue;
				} 
				stack<int> stack;
				stack.push(i);
				cout<<vertex<<"到"<<i<<"的最短路径为：";
				int j = i;
				while(this->path[j] != -1){//路径上的元素一次入栈 
					j = this->path[j];
					stack.push(j);	
				}
				//打印路径 
				cout<<stack.top();
				stack.pop(); 
				while(!stack.empty()){
					cout<<" -> "<<stack.top();
					stack.pop();
				}
				cout<<endl;
			}
		}
};

int main() 
{
	cout<<"请输入顶点数与边数："<<endl; 
	int nv ,ne;
	cin>>nv>>ne;
	Graph graph(nv,ne);
	cout<<"请输入一个起始点："<<endl;
	int vertex;
	cin>>vertex;
	if(graph.Dijikstra(vertex)){
		graph.Print_Dijikstra(vertex); 	
	}
	
	return 0;
}

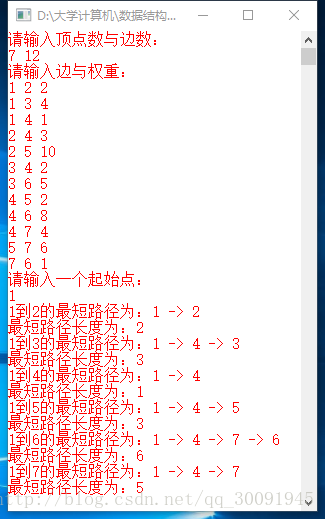
截图：
这里写图片描述

daipuweiai

关注

8
点赞
踩
42

收藏

觉得还不错? 一键收藏
打赏
6
评论
最短路径算法（上）——迪杰斯特拉（Dijikstra）算法

概述单源最短路径问题，即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前，必须弄清楚最短路径的最优子结构性质。最短路径的最优子结构性质描述为：如果P(i,j)={Vi….Vk..Vs…Vj}是从顶点i到j的最短路径，k和s是这条路径上的一个中间顶点，那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。假设P(i,j)={Vi….Vk..Vs…Vj}是从顶
复制链接

扫一扫