【总结】图的表示

---

邻接矩阵
用下标代表点的标号，以二维数组储存数值表示边的存在与否，或者边的长度大小。

邻接表
一、邻接表
邻接表是图的一种链式存储结构。
邻接表中，对图中每个顶点建立一个单链表，第i个单链表中的结点表示依附于顶点Vi的边（对有向图是以顶点Vi为尾的弧）。

二、无向图的邻接表

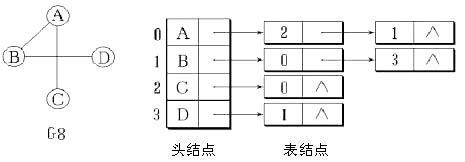
三、有向图的邻接表和逆邻接表
（一）在有向图的邻接表中，第i个单链表链接的边都是顶点i发出的边。
（二）为了求第i个顶点的入度，需要遍历整个邻接表。因此可以建立逆邻接表。
（三）在有向图的逆邻接表中，第i个单链表链接的边都是进入顶点i的边。

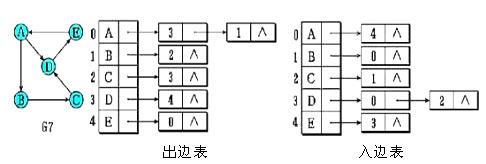
四、邻接表小结
◆ 设图中有n个顶点，e条边，则用邻接表表示无向图时，需要n个顶点结点，2e个表结点；用邻接表表示有向图时，若不考虑逆邻接表，只需n个顶点结点，e个边结点。
◆ 在无向图的邻接表中，顶点vi的度恰为第i个链表中的结点数。
◆ 在有向图中，第i个链表中的结点个数只是顶点vi的出度。在逆邻接表中的第i个链表中的结点个数为vi的入度。
◆ 建立邻接表的时间复杂度为O(n+e)。

---

两者使用途径的区别：
如果图中边的数目远远小于n2称作稀疏图，这是用邻接表表示比用邻接矩阵表示节省空间;
如果图中边的数目接近于n2,对于无向图接近于n*(n-1)称作稠密图,考虑到邻接表中要附加链域，采用邻接矩阵表示法为宜。

在空间允许情况下：
在有向图中求顶点的度采用邻接矩阵比采用邻接表表示更方便

邻接表表示中第i个边表上的结点个数就是顶点Vi的出度,求入度较困难，需遍历个顶点的边表
逆邻接表表示中第i个边表上的结点个数就是顶点Vi的入度,求出度较困难，需遍历个顶点的边表

在邻接矩阵中求边的数目必须检测整个矩阵，所消耗的时间是O(n)
在邻接表中求边的个数，只要对每个边表计数即可求得所消耗的时间是O(n+e)

---

构建代码：
邻接表：

/*
*  构建邻接表模板
*/
#include<stdio.h>
#include<string.h>
int head[100100];//表头，head[i]代表起点是i的边的编号
int cnt;//代表边的编号
struct s
{
    int u;//记录边的起点
    int v;//记录边的终点
    int w;//记录边的权值
    int next;//指向上一条边的编号
}edge[100010];
void add(int u,int v,int w)//向所要连接的表中加入边
{
    edge[cnt].u=u;
    edge[cnt].v=v;
    edge[cnt].w=w;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        int i;
        cnt=0;
        memset(head,-1,sizeof(head));//清空表头数组
        for(i=0;i<n;i++)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);
        }
        int u,v,w;
        scanf("%d",&u);
        for(i=head[u];i!=-1;i=edge[i].next)//输出所有与起点为u相连的边的终点和权值
        {
             v=edge[i].v;
             w=edge[i].w;
             printf("%d %d\n",v,w);
        }
    }
    return 0;
}

/*
*  构建邻接矩阵模板
*/
#include<stdio.h>
#include<string.h>
int G[1010][1010];//矩阵
void add(int u,int v,int w)//向邻接矩阵加入边
{
    G[u][v] = w; //有向边
}
int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        int i;
        for(i=0;i<n;i++)
        {
            int u,v,w;
            scanf("%d%d%d",&u,&v,&w);
            add(u,v,w);
        }
        //遍历全矩阵才能找到所有边
    }
    return 0;
}

---

以上部分整合于多人博客以及自己的内容：
http://blog.csdn.net/shiyanming1223/article/details/6847070
http://blog.sina.com.cn/s/blog_54b6680e010004rv.html