How Many Trees?
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Problem Description
A binary search tree is a binary tree with root k such that any node v reachable from its left has label (v) <label (k) and any node w reachable from its right has label (w) > label (k). It is a search structure which can find a node with label x in O(n log n) average time, where n is the size of the tree (number of vertices).
Given a number n, can you tell how many different binary search trees may be constructed with a set of numbers of size n such that each element of the set will be associated to the label of exactly one node in a binary search tree?
Given a number n, can you tell how many different binary search trees may be constructed with a set of numbers of size n such that each element of the set will be associated to the label of exactly one node in a binary search tree?
Input
The input will contain a number 1 <= i <= 100 per line representing the number of elements of the set.
Output
You have to print a line in the output for each entry with the answer to the previous question.
Sample Input
1 2 3
Sample Output
1 2 5
题意:首先题目介绍了二叉搜索树的概念(即在一棵二叉树中,以任意结点为根时,它的左孩子的值都小于根的值,它的右孩子的值总是大于根自身的值,这样的二叉树就是二叉搜索树),然后给你一个数字n,让你将1~n这n个数字填到结点上,问能使它成为一棵二叉搜索树的填法有多少种
首先,题目已经给出了n=1,n=2,n=3的解,我们不妨再算算看n=4的解:
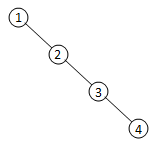
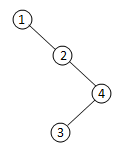
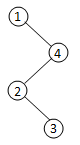
①以数字1为整棵树的根,那么有如下5种情况
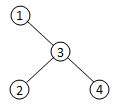
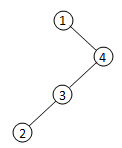
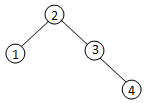
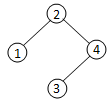
②以数字2为整棵树的根,则有如下2种情况
③以数字3为整棵树的根,因为与②是对称的,所以同样有2种情况,而以数字4为根则与①是对称的,所以有5种情况
共计14种情况
那么答案形成的就是这样一个数列
1,2,5,14……
相信知道卡特兰数的人此时都会有种似曾相识的感觉,没错,这就是卡特兰数数列,不知道卡特兰数的,可以点链接学习学习
而我们真正需要的就是卡特兰数中的一个递推式
其余就是模拟大数乘法与除法的过程,详细见代码,不明白的欢迎提出
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<stdlib.h>
#include<cmath>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 101;
const int inf = 2147483647;
const int mod = 2009;
int s[N][2*N];
int main()
{
int n,i,j,res;
s[1][1]=1;s[1][0]=1;
for(i=2;i<N;i++)
{
for(j=1;j<=s[i-1][0];j++)
{
s[i][j]+=s[i-1][j]*(4*i-2);
s[i][j+1]+=s[i][j]/10;
s[i][j]%=10;
}
while(s[i][j])
{
s[i][j+1]+=s[i][j]/10;
s[i][j]%=10;
j++;
}
for(s[i][0]=--j,res=0;j>0;j--)
{
res=res*10+s[i][j];
s[i][j]=res/(i+1);
res%=(i+1);
}
while(!s[i][s[i][0]])
s[i][0]--;
}
while(~scanf("%d",&n))
{
for(i=s[n][0];i>0;i--)
printf("%d",s[n][i]);
puts("");
}
return 0;
}









 本文探讨了如何计算由1至n的数字构成的不同二叉搜索树的数量,并揭示了其与卡特兰数的关系。
本文探讨了如何计算由1至n的数字构成的不同二叉搜索树的数量,并揭示了其与卡特兰数的关系。
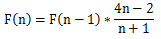

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








