HDU 5877 Weak Pair(离散化+dfs+树状数组)——2016 ACM/ICPC Asia Regional Dalian Online

本文详细解析了HDU5877 WeakPair问题的解题思路，利用离散化、DFS及树状数组等技术手段解决有根树上的弱对查找问题。介绍了如何通过遍历树节点并利用树状数组高效统计满足特定条件的节点对数量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

此文章可以使用目录功能哟↑(点击上方[+])

HDU 5877 Weak Pair

Accept: 0 Submit: 0
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)

Problem Description

You are given a rooted tree of N nodes, labeled from 1 to N. To the ith node a non-negative value ai is assigned.An ordered pair of nodes (u,v) is said to be weak if

(1) u is an ancestor of v (Note: In this problem a node u is not considered an ancestor of itself);

(2) au×av≤k.

Can you find the number of weak pairs in the tree?

Input

There are multiple cases in the data set.

The first line of input contains an integer T denoting number of test cases.

For each case, the first line contains two space-separated integers, N and k, respectively.

The second line contains N space-separated integers, denoting a1 to aN.

Each of the subsequent lines contains two space-separated integers defining an edge connecting nodes u and v , where node u is the parent of node v.

Constrains:

1≤N≤10^5

0≤ai≤10^9

0≤k≤10^18

Output

For each test case, print a single integer on a single line denoting the number of weak pairs in the tree.

Sample Input

Sample Output

1

Problem Idea

解题思路:

【题意】
给你一棵有根树,一个定值k,以及树上每个结点的值a[i]

对于有序对(u,v),如果(1)u是v的祖先,且(2)a[u]*a[v]<=k,则称该有序对(u,v)是弱的

问树中有多少对有序对(u,v)是弱的

【类型】
离散化+dfs+树状数组

【分析】
对于要求(1),u是v的祖先,我们可以采取dfs

遍历到v时,它上方的所有结点必定都是满足第一条件的u

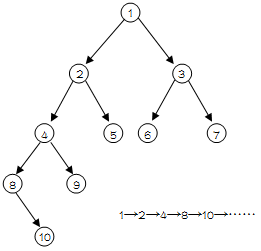
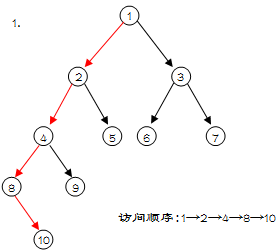
熟悉dfs过程的应该能理解这一点,不理解的可以借助下述图片稍微理解一下

从上图中,我们可以大致看出dfs过程是从树根开始向树叶访问的

对于某结点v,它的祖先u肯定是先于它被访问的,不然也不可能到达结点v

正如上图,结点10的祖先是结点1,2,4,8,不管哪个祖先,一旦有一个没被访问,也不可能达到结点10

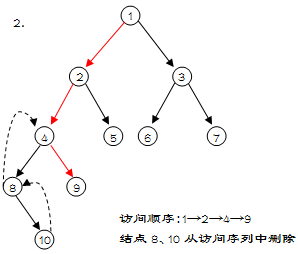
此外,在退出某个子树的时候,该子树下结点的影响会被消除,这样就能保证所有有影响的都是祖先

要求(2),a[u]*a[v]<=k，那么到v的时候,所有小于等于k/a[v]的u都满足,可以想到树状数组

结点的值a[i]最大10亿,要用树状数组的话肯定要离散化

离散化的时候要把k/a[v]加进去一起离散,保证大小关系不变

另外,当a[i]=0时,会出现除以0错误,所以我们要特判该情况

显然a[i]=0的话,任何满足要求(1)的结点都可以构成弱的有序对

所以将该条件下的k/a[i]的结果直接设置为inf

【时间复杂度&&优化】
O(n×logn×logn)

题目链接→HDU 5877 Weak Pair

Source Code

/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 20005;
const __int64 inf = 1e18+1;
const int mod = 1000000007;
struct edge
{
    int v,to;
}e[N];
int p,q,h[N],a[N],c[2*N];
bool vis[N];
__int64 k,s[2*N],ans;
void add_edge(int u,int v)
{
    e[p].v=v;
    e[p].to=h[u];
    h[u]=p++;
}
int lowbit(int t)
{//计算c[t]展开的项数
    return t&(-t);
}
void update(int i,int x)
{
    while(i<=q)
    {
        c[i]=c[i]+x;
        i+=lowbit(i);
    }
}
int Sum(int n) //求前n项的和.
{
    int sum=0;
    while(n>0)
    {
         sum+=c[n];
         n-=lowbit(n);
    }
    return sum;
}
void dfs(int x)
{
    int i;
    ans+=Sum(lower_bound(s,s+q,a[x]?k/a[x]:inf)-s+1);
    update(lower_bound(s,s+q,a[x])-s+1,1);
    for(i=h[x];i+1;i=e[i].to)
        dfs(e[i].v);
    update(lower_bound(s,s+q,a[x])-s+1,-1);
}
int main()
{
    int t,n,i,u,v;
    scanf("%d",&t);
    while(t--)
    {
        p=q=0;
        ans=0;
        memset(h,-1,sizeof(h));
        memset(c,0,sizeof(c));
        memset(vis,false,sizeof(vis));
        scanf("%d%I64d",&n,&k);
        for(i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            s[q++]=a[i];
            if(!a[i])
                s[q++]=inf;
            else
                s[q++]=k/a[i];
        }
        sort(s,s+q);
        q=unique(s,s+q)-s;
        for(i=1;i<n;i++)
        {
            scanf("%d%d",&u,&v);
            vis[v]=true;
            add_edge(u,v);
        }
        for(i=1;i<=n;i++)
            if(!vis[i])
                dfs(i);
        printf("%I64d\n",ans);
    }
    return 0;
}

菜鸟成长记