【BZOJ 2179】【FFT模板】 FFT快速傅立叶

2179: FFT快速傅立叶

Time Limit: 10 Sec Memory Limit: 259 MB
Submit: 1595 Solved: 792
[Submit][Status][Discuss]
Description

给出两个n位10进制整数x和y，你需要计算x*y。
Input

第一行一个正整数n。 第二行描述一个位数为n的正整数x。 第三行描述一个位数为n的正整数y。
Output

输出一行，即x*y的结果。
Sample Input

1

3

4

Sample Output

12

数据范围：

n<=60000

FFT模板题。

直接进行高精度乘法是$O(n^2)$的，于是我们采用FFT来$O(nlogn)$实现：
（注明：以下着重介绍算法流程和算法思想，具体细节参考《算法导论》）

1.我们把乘数的每一位看作多项式的系数，得到多项式$A(x)$（因为高精度乘法的本质就是多项式乘法）

2.首先求出$A(\omega_n^k)$，其中$k\in[0,n-1]$，$\omega_n$是n次单位复根。
由于n次单位复根的一些奇妙性质：
相消引理

折半引理

我们可以采用分治$O(nlogn)$的时间求出这$n$项的值，但是递归实现常数较大，我们采用蝴蝶算法来迭代实现。

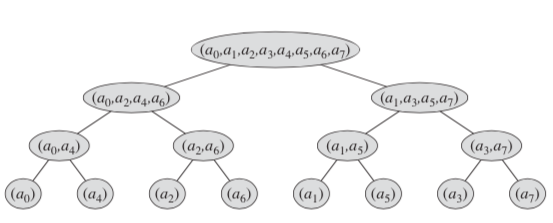
如图，把原来顺次排列的数列变成叶子中的顺序就可以迭代了~
（叶子中的顺序就是原序列的二进制逆序）

3.（这一步叫插值）
如下图，
$a_i$表示多项式的系数；
$\omega_n^k$就是我们带入多项式的值：
第一个多项式$x=\omega_n^0$，第二个是$x=\omega_n^1$，第三个是$x=\omega_n^2$….知道第n个是$x=\omega_n^{n-1}$；
$y_i$就是带入不同的$x$的求出的多项式的值。

那么，通过上一步已经求出了两个多项式（两个乘数）的$y_i$，现在我们把对应的$y_i$乘起来就是乘积的多项式的$Y_i$，我们要求的是这个多项式的系数即$a_i$，因此我们只要求出$\omega_n^k$矩阵的逆矩阵即可。

最后推出$a_i$的表达式

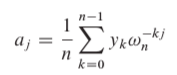
和第二步要求的式子几乎一样~再来一次FFT即可解决~
时间复杂度依然是$O(nlogn)$

详见代码注释。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <complex>
#define pi acos(-1)
#define N 200005
using namespace std;
complex<double> a[N],b[N],p[N];
int n,c[N];
char s[N];
void FFT(complex<double> x[],int n,int p)
{
//把原来依次排列的数变成叶子中的顺序
    for (int i=0,t=0;i<n;i++)
    {
        if (i>t) swap(x[i],x[t]);
        for (int j=n>>1;(t^=j)<j;j>>=1);
    }
    for (int m=2;m<=n;m<<=1)  //枚举每一层
    {
        complex<double>       wn(cos(p*2*pi/m),sin(p*2*pi/m));
        for (int i=0;i<n;i+=m)
        {
            complex<double> w(1,0),u;
            int k=m>>1;
            for (int j=0;j<k;j++,w*=wn)
            {
            //蝴蝶操作
                u=x[i+j+k]*w;
                x[i+j+k]=x[i+j]-u;
                x[i+j]=x[i+j]+u;
            }
        }
    }
}
int main()
{
    cin>>n;
    scanf("%s",s);
    for (int i=0;i<n;i++)
        a[i]=s[n-i-1]-'0';
    scanf("%s",s);
    for (int i=0;i<n;i++)
        b[i]=s[n-i-1]-'0';
    //把长度变为2的幂次，方便FFT中的迭代
    for (int j=n,i=1;(i>>2)<j;i<<=1)  
        n=i;     
    FFT(a,n,1),FFT(b,n,1);
    for (int i=0;i<n;i++)
        p[i]=a[i]*b[i];
    //插值
    FFT(p,n,-1);
    for (int i=0;i<n;i++)
        c[i]=p[i].real()/n+0.1;
    int len=0;
    //进位
    for (int i=0;i<n;i++)
        if (c[i])
            len=i,c[i+1]+=c[i]/10,c[i]%=10;
    for (int i=len;i>=0;i--)
        printf("%d",c[i]);
    return 0;
}