有上下界的网络流问题

写在前面

有上下界的网络流即对边的流量有限制，必须在$[down,up]$的范围内。

其实普通的网络流也是一种特殊的有上下界的网络流，只是每条边的流量限制为$[0,cap]$。

分类

有上下界的网络流分为两种：

• 有源汇
  所有点都要求满足流量平衡

• 无源汇
  除了源点汇点都要满足流量平衡（源点只有流出，汇点只有流入）

无源汇

可行流

我们可以想到为了满足流量的下限$down$，可以直接将边的流量设为$up-down$。

但是我们求出这个图的最大流之后，加上下限$down$，会使得某些点不满足流量平衡。

这该怎么解决呢？

我们可以建立附加源和附加汇，来补充和吸收这些流量。

具体来说就是：

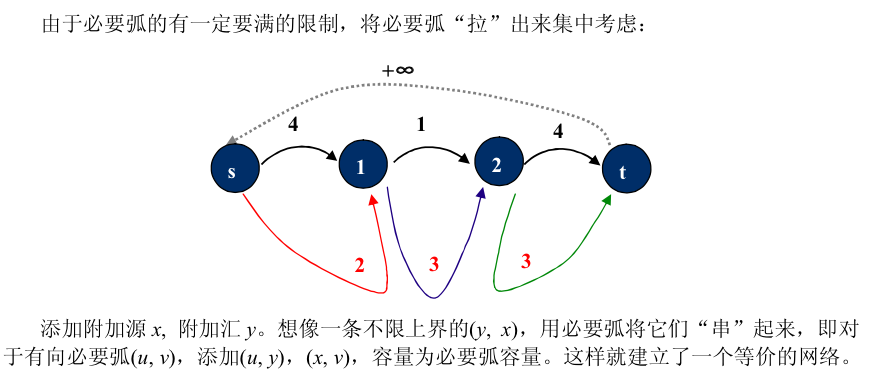
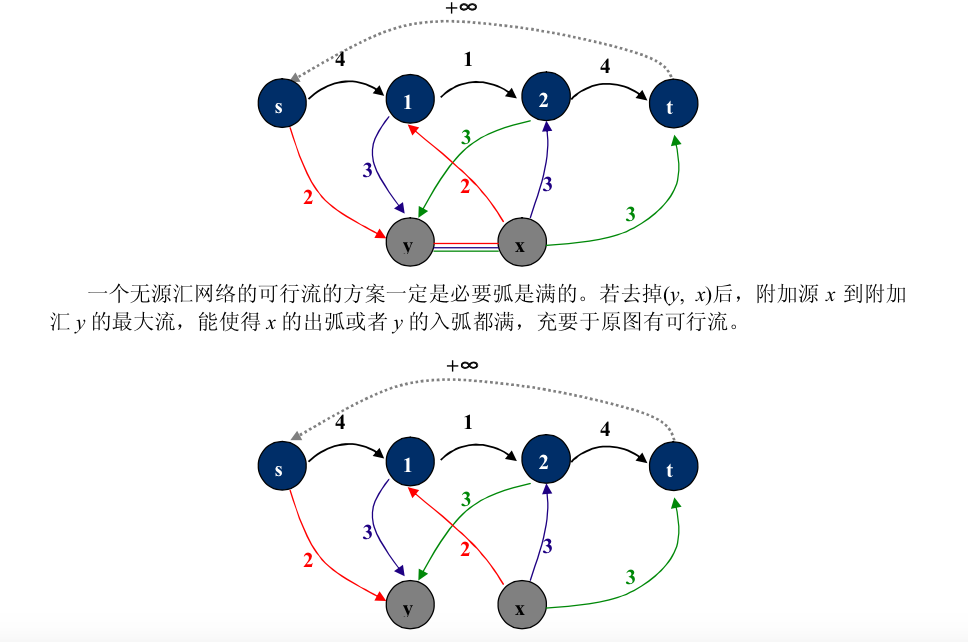
from 《图论原理 胡伯涛》

因此，对于一条边u->v，我们在新图中连三条边：

• u->v $cap=up-down$
• S->v $cap=down$
• u->T $cap=down$

对于这个图求最大流，然后判断最大流是否等于$\sum down_i$，如果等于就是可行流，否则没有可行流。

• 例题 SGU 194

*注:由于是无源汇的，所以并没有最大流最小流之说。

有源汇

可行流

我们连一条t->s,流量限制为$[0,inf]$的边，有源汇就变成了无源汇，像上面一样求解即可。

• 例题 POJ 2396

最小流

• <法一>
  好理解，时间复杂度较高。

  • 因为s->t的流量与t->s的流量是相等的，我们可以通过限制t->s的流量来确定此时网络中的流量。
  • 因此使用二分来求解
  • 当前的二分范围是$[l,r],mid=\frac {l+r}2$；如果t->s的流量设为$mid$，存在可行流，那么缩小上限即$r=mid$

• <法二>
  较难理解，时间复杂度低。

  • 先不要连接t->s流量为$inf$的边，求一次最大流

  • 再连上t->s流量为$inf$的边，在残量网络上求一次最大流

  • 为什么这样做呢？

  • 感性的来理解，第一步中求最大流，所有能流的边都“竭尽全力”的流完了；
    第二步再求最大流的时候，t->s上的流量就会尽可能的小（即s->t的流量尽可能小）

• 例题 SGU 176

• 例题 BZOJ 1458

最大流

• <法一>
  与最小流中的二分法类似，只是变成了可行就调高下限。

• <法二>

  • 连上t->s流量为$inf$的边，求一次附加源到附加汇的最大流
  • 在残量网络上求一次s到t的最大流

  • 最后答案就是第二次求出的最大流（因为第一次求出的最大流是t->s的流量，而这个流量在他的反向边s->t中出现，所以不需要另外加上）

  • 为什么这样做呢？

  • 依然感性的理解，第一次求出的(附加源到附加汇的)最大流是为了满足$down$尽可能流满，然而此时s->t上可能还有可行的流，我们在残量网络上继续来求最大流，可以使得最后求出的流既满足$\ge down$的限制，且最大。

欢迎指正错误~