[LeetCode40]Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

Analysis:

想了半天，也想不出来O(n)的解法，于是上网google了一下。
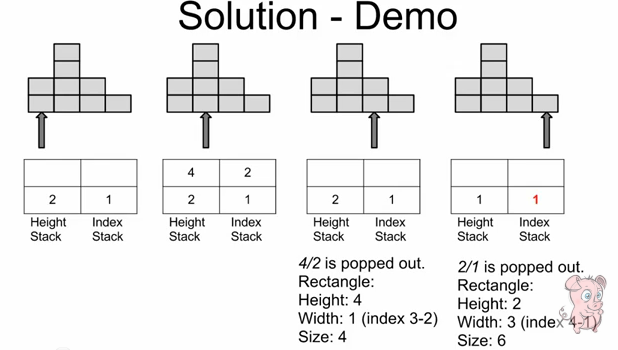
如下图所示，从左到右处理直方，i=4时，小于当前栈顶（及直方3），于是在统计完区间[2,3]的最大值以后，消除掉阴影部分，然后把红线部分作为一个大直方插入。因为，无论后面还是前面的直方，都不可能得到比目前栈顶元素更高的高度了。

这就意味着，可以维护一个递增的栈，每次比较栈顶与当前元素。如果当前元素小于栈顶元素，则入站，否则合并现有栈，直至栈顶元素小于当前元素。结尾入站元素0，重复合并一次。

Case 1: current > previous (top of height stack)
Push current height and index as candidate rectangle start position.

Case 2: current = previous
Ignore.

Case 3: current < previous
Need keep popping out previous heights, and compute the candidate rectangle with height and width (current index - previous index). Push the height and index to stacks.

(Note: it is better use another different example to walk through the steps, and you will understand it better).

Java

int area = 0;
        if(height.length<=0) return area;
        if(height.length==1) return height[0];
        height = Arrays.copyOf(height, height.length+1);
        height[height.length-1]=0;
        Stack<Integer> index = new Stack<>();
        int i=0;
        while(i<height.length){
        	if(index.empty() || height[i]>=height[index.peek()]) index.push(i++);
        	else {
				int temp = index.pop();
				area = Math.max(area, height[temp]*(index.empty()?i:i-index.peek()-1));
			}
        }
        return area;

c++

int largestRectangleArea(vector<int> &height) {
        int maxArea = 0;
    height.push_back(0);
    stack<int> stk;
    int i=0;
    while(i<height.size()){
        if(stk.empty() || height[stk.top()] <= height[i])
            stk.push(i++);
        else{
            int t = stk.top();
            stk.pop();
            maxArea = max(maxArea, height[t]*(stk.empty()? i:i-stk.top()-1));
        }
    }
    return maxArea;
    }