平衡二叉树

对于二叉查找树，尽管查找、插入及删除操作的平均运行时间为O(logn)，但是它们的最差运行时间都是O(n),原因在于对树的形状没有限制。
平衡二叉树又称为AVL树，它或者是一棵空树，或者是有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左右子树的深度之差的绝对值不超过1。二叉树的的平衡因子BF为：该结点的左子树的深度减去它的右子树的深度，则平衡二叉树的所有结点的平衡因子为只可能是：-1、0和1。
一棵好的平衡二叉树的特征：
（1）保证有n个结点的树的高度为O(logn)
（2）容易维护，也就是说，在做数据项的插入或删除操作时，为平衡树所做的一些辅助操作时间开销为O(1)。
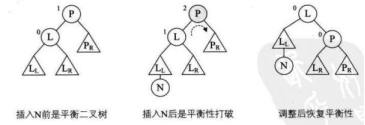
在一棵二叉查找树中插入结点后，调整其为平衡二叉树。若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。首先要找出插入新结点后失去平衡的最小子树根结点的指针。然后再调整这个子树中有关结点之间的链接关系，使之成为新的平衡子树。当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整，整个二叉排序树就又成为一棵平衡二叉树。

1. 调整方法
   
   • 插入点位置必须满足二叉查找树的性质，即任意一棵子树的左结点都小于根结点，右结点大于根结点
   • 找出插入结点后不平衡的最小二叉树进行调整，如果是整个树不平衡，才进行整个树的调整。
2. 调整方式
   
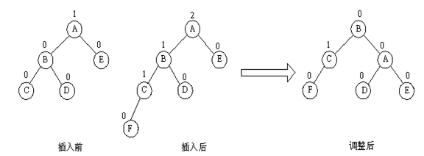
   • LL型（单右旋）：插入位置为左子树的左结点，进行向右旋转。
     
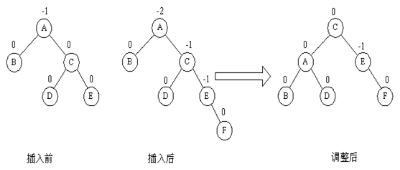
     由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1变为2，成为不平衡的最小二叉树根结点。此时A结点顺时针右旋转，旋转过程中遵循“旋转优先”的规则，A结点替换D结点成为B结点的右子树，D结点成为A结点的左孩子。
   • RR型（单左旋）：插入位置为右子树的右孩子，进行向左旋转。
     
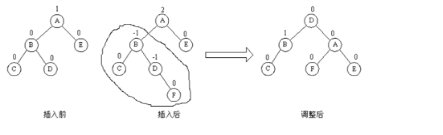
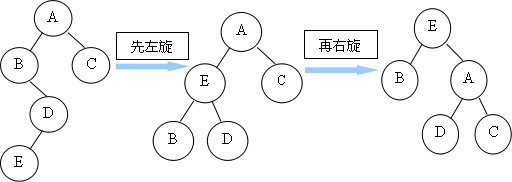
     由于在A的右子树C的右子树插入了结点F，A的平衡因子由-1变为-2，成为不平衡的最小二叉树根结点。此时，A结点逆时针左旋转，遵循“旋转优先”的规则，A结点替换D结点成为C的左子树，D结点成为A的右子树。
   • LR型（先左旋后右旋）：插入位置为左子树的右孩子，要进行两次旋转，先左旋转，再右旋转；第一次最小不平衡子树的根结点先不动，调整插入结点所在的子树，第二次再调整最小不平衡子树。
     
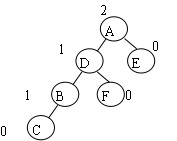
     由于在A的左子树B的右子树上插入了结点F，A的平衡因子由1变为了2，成为不平衡的最小二叉树根结点。第一次旋转A结点不动，先将B的右子树的根结点D向左上旋转提升到B结点的位置，如下图：
     
     然后再把该D结点向右上旋转提升到A结点的位置。
   • RL型（先右旋后左旋）：插入位置为右子树的左孩子，进行两次调整，先右旋转再左旋转；处理情况与LR类似。
     
   • 单右旋操作
     
     
   • 左平衡旋转处理
     
     
     对于switch(Lr->bf)的3种情况：LH，EH,RH，下面分情况介绍（这里思考了好久）
     
     • case LH(左子树高)
       
     • case EH（左右等高）
       
     • case RH (右子树高)