《Thinking In Algorithm》10.树的三种遍历（递归与非递归实现）

1：深度优先

1.1：前序遍历

1. Visit the root.
2. Traverse the left subtree.
3. Traverse the right subtree.

如下图：

Pre-order: F, B, A, D, C, E, G, I, H

伪代码：

preorder(node) if node == null then return visit(node) preorder(node.left) preorder(node.right)

iterativePreorder(node) parentStack = empty stack parentStack.push(null) top = node while ( top != null ) visit( top ) if ( top.right != null ) parentStack.push(top.right) if ( top.left != null ) parentStack.push(top.left) top = parentStack.top(); parentStack.pop();

1.2：中序遍历

1. Traverse the left subtree.
2. Visit root.
3. Traverse the right subtree.

In-order: A, B, C, D, E, F, G, H, I

伪代码：

inorder(node) if node == null then return inorder(node.left) visit(node) inorder(node.right)

iterativeInorder(node) parentStack = empty stack while (not parentStack.isEmpty() or node ≠ null) if (node ≠ null) parentStack.push(node) node = node.left else node = parentStack.pop() visit(node) node = node.right

1.3：后序遍历

1. Traverse the left subtree.
2. Traverse the right subtree.
3. Visit the root.

Post-order: A, C, E, D, B, H, I, G, F

伪代码

postorder(node) if node == null then return postorder(node.left) postorder(node.right) visit(node)

iterativePostorder(node) parentStack = empty stack lastnodevisited = null while (not parentStack.isEmpty() or node ≠ null) if (node ≠ null) parentStack.push(node) node = node.left else peeknode = parentStack.peek() if (peeknode.right ≠ null and lastnodevisited ≠ peeknode.right) /* if right child exists AND traversing node from left child, move right */ node = peeknode.right else parentStack.pop() visit(peeknode) lastnodevisited = peeknode

1.4：java代码实现三种遍历

树的结构是

                                            10
                                           /   \
                                          5     12
                                        /   \   
                                     4       7 

代码中我主要解释下让我一直纠结的递归法了，总是对递归法执行的顺序有疑惑。详细可以看《Thinking In Algorithm》09.彻底理解递归

public class Preorder{	
	/*******************************递归法****************************/
	//递归前序遍历		print：10,5,4,7,12
	public static void preorder(TNode node){
		if(node!=null){
			System.out.println(node.getValue()) ;
			preorder(node.getLeft()) ;
			preorder(node.getRight()) ;
		}
	}
	//递归中序遍历		print: 4,5,7,10,12
	public static void inorder(TNode node){
		if(node!=null){
			inorder(node.getLeft()) ;
			System.out.println(node.getValue()) ;
			inorder(node.getRight()) ;
		}
	}
	//递归后序遍历		print: 4,7,5,12,10
	public static void postorder(TNode node){
		if(node!=null){
			postorder(node.getLeft()) ;
			postorder(node.getRight()) ;
			System.out.println(node.getValue()) ;
		}
	}
	
	/*******************************非递归*****************************/
	//非递归前序遍历		print：10,5,4,7,12
	public static void iterativePreorder(TNode node){
		MyStack parentStack = new MyStack() ;
		parentStack.push(node) ;
		while(!parentStack.isEmpty()){
			TNode temp = parentStack.getFirst().getValue() ;
			System.out.println(temp.getValue()) ;
			parentStack.pop() ;
			if(temp.getRight()!=null){ parentStack.push(temp.getRight()) ;}
			if(temp.getLeft()!=null){ parentStack.push(temp.getLeft()) ;}
		}
	}
	//非递归中序遍历		print: 4,5,7,10,12
	public static void iterativeInorder(TNode node){
		MyStack  mystack = new MyStack() ;
		while(!mystack.isEmpty()||node!=null){
			if(node!=null){
				mystack.push(node) ;
				node = node.getLeft() ;
			}else{
				node = mystack.pop().getValue() ;
				System.out.println(node.getValue()) ;
				node = node.getRight() ;
			}
		}
	}
	//非递归后序遍历		print: 4,7,5,12,10
	public static void iterativePostorder(TNode node){
		MyStack  mystack = new MyStack() ;
		TNode temp = null ;
		TNode peeknode = null ;
		while(!mystack.isEmpty()||node!=null){
			if(node!=null){
				mystack.push(node) ;
				node = node.getLeft() ;
			}else{
				peeknode = mystack.getFirst().getValue() ;
				if(peeknode.getRight()!=null&&temp!=peeknode.getRight()){
					node = peeknode.getRight() ;
				}else{
					mystack.pop() ;
					System.out.println(peeknode.getValue()) ;
					temp = peeknode ;
				}
			}
		}
	}
	
	public static void main(String args[]){
		MyTree mytree = new MyTree() ;
		mytree.insert(10) ;
		mytree.insert(5);
		mytree.insert(12);
		mytree.insert(4);
		mytree.insert(7);
		
		preorder(mytree.getRoot()) ;
		inorder(mytree.getRoot()) ;
		postorder(mytree.getRoot()) ;
		
		iterativePreorder(mytree.getRoot()) ;
		iterativeInorder(mytree.getRoot()) ;
		iterativePostorder(mytree.getRoot()) ;
	}
}
/*****************二叉树的实现****************/
class TNode{
	private int value ;
	private TNode left ;
	private TNode right ;
	
	public TNode(int value){ this.value = value ;}
	public void setLeft(int value){ this.left = new TNode(value) ;}
	public void setRight(int value){ this.right = new TNode(value) ;}
	public TNode getLeft(){ return this.left ;}
	public TNode getRight(){ return this.right ;}
	public int getValue(){ return this.value ;}
}
class MyTree{
	private TNode root ;
	
	public void setRoot(int value){ this.root = new TNode(value) ;}
	public TNode getRoot(){ return this.root ;}
	public void insert(int value){
		TNode x = this.root ;
		TNode y = null ;
		while(x!=null){
			y = x ;
			if(value<x.getValue()){ x = x.getLeft() ;}
			else{ x = x.getRight() ;}
		}
		
		if(y == null){ setRoot(value) ;}
		else if(value<y.getValue())
		{ y.setLeft(value) ;}
		else{ y.setRight(value) ;}
	}
}

/*****************栈的实现****************/
class StackNode{  
        public TNode item ;  
        public StackNode next ;  
		
        public StackNode(){ ;}
		public StackNode(TNode item){ this.item = item ;}
        public TNode getValue(){ return item ;}  
}  
class MyStack{  
    int N ; //size of myStack  
    StackNode first ; // the top of stack  
      
      
    //size of mystack  
    public int size(){ return N ;}  
      
    //empty or not  
    public boolean isEmpty(){ return N==0 ;}  
	
	public StackNode getFirst(){ return this.first ;}
      
	public void push(TNode item){
		if(isEmpty()){
			first = new StackNode() ;  
			first.item = item;  
			N++; 
		}else{
			StackNode oldfirst = first;  
			first = new StackNode() ;  
			first.item = item;  
			first.next = oldfirst;  
			N++; 
		}
		
	}
    public StackNode pop(){
		StackNode top = first ;
        first = first.next;            // delete first node  
        N--;  
		return top ;
	}
}

2.广度遍历

广度遍历比较简单，就是层次遍历

                

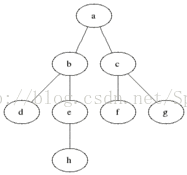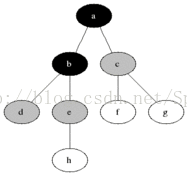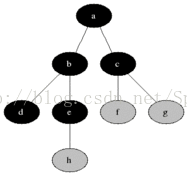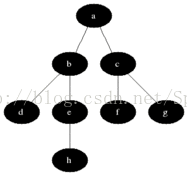
伪代码

levelorder(root)
  q = empty queue
  q.enqueue(root)
  while not q.empty do
    node := q.dequeue()
    visit(node)
    if node.left ≠ null then
      q.enqueue(node.left)
    if node.right ≠ null then
      q.enqueue(node.right)