字符串匹配算法

算法的改进主要是针对如果出现不匹配字符，应该怎样回退的问题

定义

在母字符串中找子字符串，如果找到返回字串在母字符串中的位置，如果没有找到，返回-1。
参见 leetcode 28. Implement strStr()

朴素的匹配算法

逐个跟字串匹配。

失败则子串向前移动一位，继续比较

顺序匹配字串与母串的每一个字符
- 如果达到子字符串末尾，就返回母串中子串首字符对应位置
- 如果遇到不匹配字符就回退到子串首字符对应母串的位置的下一个字符进行比较

public class Solution {
    public int strStr(String haystack, String needle) {
        if(needle==null || needle.length()==0){
            return 0;
        }
        int p =0;
        for(int i=0; i<haystack.length(); i++){
            if(haystack.charAt(i)==needle.charAt(p)){
                p++;
            }else{
                i-=p;
                p =0;
            }
            if(p==needle.length()){
                return i-p+1;
            }
        }
        return -1;
    }
}

KMP算法

KMP算法的核心是一个字串回退数组next,来确定当字符不匹配时字串的回退位置，这个数组只与字串特征有关，表示前缀与后缀的最大匹配长度。

- 如果已匹配部分后缀与前缀匹配长度为零，那就只能直接跳过已匹配部分
- 如果已匹配部分后缀与前缀有匹配部分，那么就将字串指针跳到字串已匹配部分前缀与后缀最大匹配长度位置
- 如果下一个字符还是不匹配，重复上面的跳转，直到p为零

关键算法：求next数组
求next数组也就是求字串到当前位置的前缀后缀最大匹配长度，本算法精彩之处是用了相当于两个字串进行匹配的方法来求前缀与后缀的最大匹配长度。求下一个最大匹配长度时
- 首先将另一字串置于字串最大匹配部分
- 如果新的字符不匹配，就找已匹配部分的最大匹配长度，然后对比新字符，就像KMP算法匹配字符串

public class Solution {
    public static void main(String[] args) {
        String haystack = "hello, how are you";
        String needle = "how";
        System.out.println(strStr(haystack,needle));
    }

    public static int strStr(String haystack, String needle){
        int[] next = getNext(needle);
        for(int i=0,j=0; i<haystack.length(); i++){
            while(j>0 && haystack.charAt(i)!=needle.charAt(j)){
                j=next[j-1];
            }
            if(haystack.charAt(i)==needle.charAt(j)){
                j++;
            }
            if(j==needle.length()){
                return i-j+1;
            }
        }
        return -1;
    }
    public static int[] getNext(String needle){
        int[] next = new int[needle.length()];
        next[0] = 0;
        for(int i=1,j=0; i<next.length; i++){
            while(j>0 && needle.charAt(i)!=needle.charAt(j)){
                j = next[j-1];
            }
            if(needle.charAt(i)==needle.charAt(j)){
                j++;
            }
            next[i] = j;
        }
        return next;
    }
}  

Rabin_Karp算法

• 该算法核心是将字符串的比较转化为其对应的Hash值的比较，关键在于如何根据母串中P[s,s+m]的Hash值在O（1）的时间内计算出P[s+1,s+1+m]的Hash值。
• 算法复杂度最坏为O((n-m+1)*m)，出现在Hash碰撞比较多的时候， 但是平均复杂度为O(n)
• 如下为一个简单的数字匹配算法，关键算法hash = ((hash-(source.charAt(i)-'0')*h) * 10 + source.charAt(i+m) - '0')%q

public class Demo {
    public static void main(String[] args) {
        String haystack = "1012132343";
        String needle = "12";
        System.out.println(indexOfRK(needle, haystack));
    }
    public static int indexOfRK(String sub, String source) {
        int m = sub.length();
        int n = source.length();

        long h = 1;
        long q = 127;
        for(int i=0; i<m-1; i++){
            h=h*10%q;
        }

        long subHash = 0;
        long hash = 0;

        for (int i = 0; i < m; i++) {
            subHash = (subHash * 10 + sub.charAt(i) - '0')%q;
            hash = (hash * 10 + source.charAt(i) - '0')%q;
        }
        for (int i = 0; i <= n - m; i++) {
            if (subHash == hash && check(sub, source, i)) {
                return i;
            }
            if (i < n - m) {
                hash = ((hash-(source.charAt(i)-'0')*h) * 10 + source.charAt(i+m) - '0')%q;
                if(hash<0){
                    hash+=q;
                }
            }
        }
        return -1;
    }

    private static boolean check(String sub, String source, int index) {
        for (int i = index, j = 0; j < sub.length(); i++, j++) {
            if (source.charAt(i) != sub.charAt(j)) {
                return false;
            }
        }
        return true;
    }
}  

BM算法

（1）坏字符算法

当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对，然后继续匹配。坏字符算法有两种情况。

Case1：模式串中有对应的坏字符时，让模式串中最靠右的对应字符与坏字符相对（PS：BM不可能走回头路，因为若是回头路，则移动距离就是负数了，肯定不是最大移动步数了），如下图。

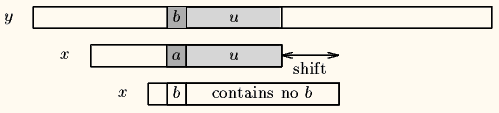
Case2：模式串中不存在坏字符，很好，直接右移整个模式串长度这么大步数，如下图。

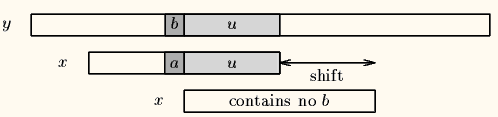
（2）好后缀算法

如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀或后缀的部分, 那把下一个后缀或部分移动到当前后缀位置。假如说，pattern的后u个字符和text都已经匹配了，但是接下来的一个字符不匹配，我需要移动才能匹配。如果说后u个字符在pattern其他位置也出现过或部分出现，我们将pattern右移到前面的u个字符或部分和最后的u个字符或部分相同，如果说后u个字符在pattern其他位置完全没有出现，很好，直接右移整个pattern。这样，好后缀算法有三种情况，如下图所示：

Case1：模式串中有子串和好后缀完全匹配，则将最靠右的那个子串移动到好后缀的位置继续进行匹配。

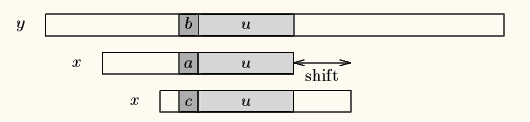
Case2：如果不存在和好后缀完全匹配的子串，则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。

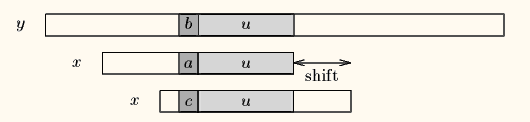
Case3：如果完全不存在和好后缀匹配的子串，则右移整个模式串。

（3）移动规则

BM算法的移动规则是：

将3中算法基本框架中的j += BM()，换成j += MAX（shift（好后缀），shift（坏字符）），即

BM算法是每次向右移动模式串的距离是，按照好后缀算法和坏字符算法计算得到的最大值。

shift（好后缀）和shift（坏字符）通过模式串的预处理数组的简单计算得到。坏字符算法的预处理数组是bmBc[]，好后缀算法的预处理数组是bmGs[]。

相关文章1
相关文章2