线性表的插入排序

插入排序算法思想：每趟一个元素，按其关键字的大小插入到他前面已经排序的子序列中，依次重复，直到插入全部元素。

插入排序算法有直接插入排序，二分插入排序，希尔排序。

- 直接插入排序

private static void insertSort(int[] keys) {
        for (int i = 1; i < keys.length; i++) {
            int temp = keys[i],j;//temp将要和前面排序好的数组比较,j是i前面的那个数
            for ( j = i-1; j >= 0 &&temp<keys[j]; j--) {
                //如果需要比较的那个比前面的那个值小，较大的那个向后移动
                keys[j+1] = keys[j];
            }
            keys[j+1] = temp;
        }
    }

temp就是将要插入前面已经排序好数组的一个值，如果这个值比较他前面那个数比较小，（如果比较大证明这个排序是成功的，开始下一个值的比较）就把前面那个值往后移动一位，然后再拿他和前面的前面那个开始比较（通过移动j角标），重复上述步骤。

• 稳定排序
• 时间复杂度效率在O(n)和O(n²)之间
• 空间复杂度是O(1)占用了一个temp存储单元

- 二分插入排序

直接插入排序的每一趟，将一个元素a_i插入到他前面的一个排序的子序列中，其中采用顺序查找算法寻找a_i的插入位置，此时，子序列是顺序存储而且是排序好的，这两条正好符合二分查找的要求。因此用二分查找法代替插入排序中的顺序查找，就叫做二分法插入排序。

private static void insertSort2(int[] keys) {
        int i, j, temp, low, mid, high;
        for (i = 1; i < keys.length; i++) {
            low = 0;// 已排序好的数组的最小角标
            high = i - 1;// 已排序好的数组的最大角标
            temp = keys[i];// 将要插入已排序好数组的数字
            while (low <= high) {

                mid = (low + high) / 2; // 折中,取中间位置
                if (keys[mid] > temp) // 判断要插入的元素和中间元素的大小
                    high = mid - 1; // 中间元素大,最高位置取当前中间位置的前一位,重新再求中间位置
                else
                    low = mid + 1; // 中间元素小,最高位置取当前中间位置的后一位,重新再求中间位置

            }
             for(j=i-1;j>high;j--)   //将(high+1)～i的所有元素后移一位  
                 keys[j+1]=keys[j];        
             keys[high+1]=temp;        //插入元素  
        }
    }

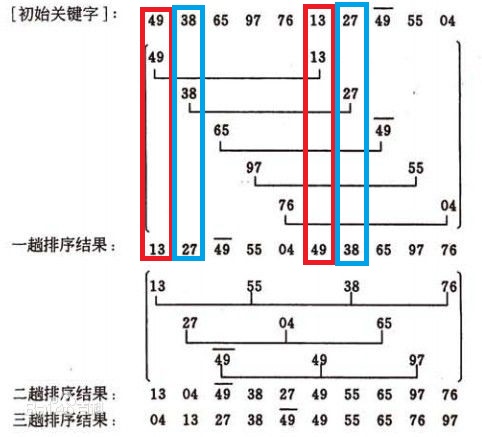
- 希尔排序

由直接排序算法分析可知，若数据序列越接近有序，则时间效率越高，n较小时，时间效率也较高。希尔排序正是基于这两点对直接排序算法进行增进。
希尔算法算法描述如下：
- 将一个数据序列分成若干组，每组由若干相隔一段距离（称为增量）的元素组成，在一个组内采用直接插入的排序算法进行排序。
- 增量初始值通常为数据序列长度的一半，以后每趟增量递减一般，最后为1。随着增量逐渐减小，组数也减少，组内元素个数增加，增加序列接近有序。

    private static void shellSort(int[] keys) {
        for (int delta = keys.length/2; delta > 0; delta/=2) {//若干趟，控制增量每趟减半
            for (int i = delta; i < keys.length; i++) {//一趟分为若干组，每组直接插入排序
                int temp = keys[i],j;
                for (j = i-delta; j >=0&&temp< keys[j]; j-=delta) {
                    keys[j+delta] = keys[j];
                }
                keys[j+delta] = temp;//插入元素
            }
        }
    }

• 时间复杂度的下界是n*log2n
• 空间复杂度为O（1）
• 由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。