平衡二叉树总结二：avl树

最新推荐文章于 2022-03-27 15:51:23 发布
最新推荐文章于 2022-03-27 15:51:23 发布
阅读量349 收藏
点赞数
分类专栏： 平衡二叉树 文章标签： 数据结构 算法 二叉树 搜索
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/tdscdma123/article/details/53998113
版权

  avl树是第一个创造出来的平衡二叉树，之后很多的平衡树都是基于AVL树的基本操作——旋转来实现的。

avl树结构如下：

struct avl{
  avl* left;
  avl* right;
  int val,h;//val值域，h高度。
};
typedef avl* tree;
//获取高度的函数
int height(tree t){
  if(t==NULL)return -1;
  else{return t->h;}
}

  一、旋转操作（所有旋转操作都能保证不破坏有序性）

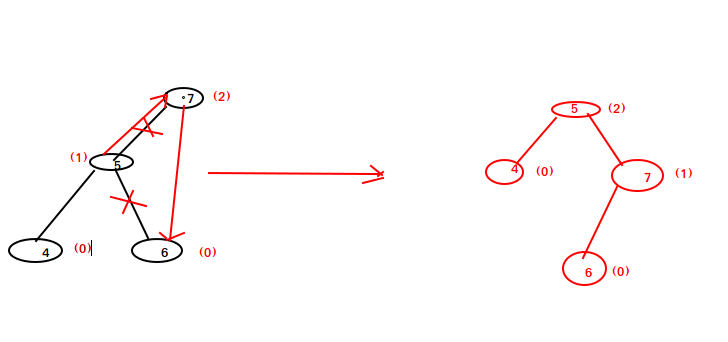
  1.左单旋（LL)。

  当左子树高度-右子树高度 >= 2 并且 左子树的左儿子高度 >= 右儿子时，可通过左单旋操作平衡树高度。

 

     linux下面实在没找到好的画图软件，凑或看吧

  上图中，旋转前，左子树高度为1，右子树高度为-1（NULL），旋转后，左子树高度为0右子树高度为1，并且旋转后依然是二叉搜索树。操作代码如下：

/*旋转操作不会改变二叉搜索树的有序性，即左<中<右。
它只会调整左右子树的高度差，高的降低，低的提高。*/
//LL旋转（左单旋）
tree LL(tree t){
  tree t1 = t->left;
  t->left = t1->right;
  t1->right = t;
//调整后t,t1的高度都会改变，但是t的子树高度未变，先
//调整它。
  t->h = max(height(t->left),height(t->right))+1;
//再调整t1
  t1->h = max(height(t1->left),height(t1->right))+1;
  return t1;
}
//RR旋转，LL操作的对称。
tree RR(tree t){
  tree t1 = t->right;
  t->right = t1->left;
  t1->left = t;
//调整后t,t1的高度都会改变，但是t的子树高度未变，先
//调整它。
  t->h = max(height(t->left),height(t->right))+1;
//再调整t1
  t1->h = max(height(t1->left),height(t1->right))+1;
  return t1;
}
2.左双旋

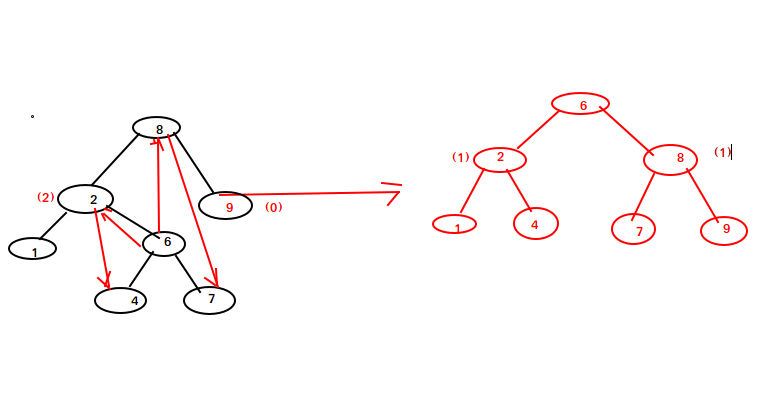
  当左子树高度-右子树高度 >= 2 并且 左子树的左儿子高度 < 右儿子时，可通过左双旋操作平衡树高度。

  如图，先把节点6的左儿子赋值给2节点的右儿子，右儿子赋值给节点8的左儿子，再将其左右儿子分别设为2节点与8节点。这样操作后，树的左右儿子高都变为了1。

  说的挺复杂，但是代码却出奇的简单。

//LR旋转，左双旋，虽然我也没明白为啥LR.
tree LR(tree t){
  t->left = RR(t->left);
  return LL(t);
}

//RL旋转
tree RL(tree t){
   t->right = LL(t->right);
  return RR(t);
}
3.右单旋，右双旋。

  这两个操作是左旋的镜像操作，代码已经在上面给出了。

4.插入

  插入操作有些复杂，主要在二叉搜索树的插入操作基础上，需要添加调整高度的代码。

/*比较难一点的插入操作*/
tree insert(tree t,int val){
  if(t==NULL){//插入到叶节点上。
    t = new avl;
    t->val = val;
    t->left = t->right = NULL;
    t->h = 0;
    return t;
  }
  if(val > t->val){//走右边
    t->right = insert(t->right,val);
    if(height(t->right)-height(t->left)==2){//判断是否
//违反高度平衡条件。
      if(val > t->right->val){//如果走的子树右边
        t = RR(t);
      }
      else{//走的子树左边
        t = RL(t);
      }
    }
  }
  else{
    t->left = insert(t->left,val);
 //判断平衡条件
    if(height(t->left)-height(t->right)==2){
      if(val < t->left->val){
        t = LL(t);
      }
      else{
        t = LR(t);
      }
    }
  }
  t->h = max(height(t->left),height(t->right))+1;
  return t;
}

5.最难的就是删除操作了，数据量不大时还是建议使用lazy 删除。

  

/*永远都最难的删除。*/
tree del(tree t,int val){
//首先找到需删除的节点。
  tree v;
  if(t==NULL)return NULL;//为空说明没找到该值。
  if(val > t->val){//往右走。
    t->right = del(t->right,val);
    //删除可能会破坏平衡条件，调整，往右走，右子树可能变低。
    if(height(t->left) - height(t->right) == 2){
      if(height(t->left->left) >= height(t->left->right)){
        t = LL(t);
      }
      else{ t = LR(t);}
    }
  }
  else if(val < t->val){
    t->left = del(t->left,val);
    //左子树可能变低。
    if(height(t->right) - height(t->left) == 2){
      if(height(t->right->right) >= height(t->right->left)){
        t = RR(t);
      }
      else{ t = RL(t);}
    }
  }
  else{
    if(t->left == NULL){//只有一个儿子时，可以直接把另一个儿子接上来。
      v = t->right;delete t;
      return v;
    }
    else if(t->right == NULL){
      v = t->left;delete t;
      return v;
    }
    else{//双儿子时，查找左子树最大值。
      v = findMax(t->left);
      if(v == t->left){//刚好是左儿子，直接把左儿子右子树接上来。
        t->left = v->left;
        t->val = v->val;
        delete v;//调整高度。
        t->h = max(height(t->left),height(t->right))+1;
      }
      else{//否则删除把最大值赋值给t，递归删除最大值，因为此时
      //最大值必定没有右儿子。
        t->val = v->val;
        del(t->left,v->val);
      }
    }
  }
  return t;
}
//avl树的删除编程起来确实异常复杂，所以实际上大家也很少用这种树，工程里更多是红黑树
//以及splay，比赛更多是编码简单的treap，sbt等。

 6.最后汇总一下，加了一些测试代码。 

#include<iostream>
#include<queue>
using namespace std;

struct avl{
  avl* left;
  avl* right;
  int val,h;//val值域，h高度。
};
typedef avl* tree;
int height(tree t){
  if(t==NULL)return -1;
  else{return t->h;}
}
/*旋转操作不会改变二叉搜索树的有序性，即左<中<右。
它只会调整左右子树的高度差，高的降低，低的提高。*/
//LL旋转（左单旋）
tree LL(tree t){
  tree t1 = t->left;
  t->left = t1->right;
  t1->right = t;
//调整后t,t1的高度都会改变，但是t的子树高度未变，先
//调整它。
  t->h = max(height(t->left),height(t->right))+1;
//再调整t1
  t1->h = max(height(t1->left),height(t1->right))+1;
  return t1;
}
//RR旋转，LL操作的对称。
tree RR(tree t){
  tree t1 = t->right;
  t->right = t1->left;
  t1->left = t;
//调整后t,t1的高度都会改变，但是t的子树高度未变，先
//调整它。
  t->h = max(height(t->left),height(t->right))+1;
//再调整t1
  t1->h = max(height(t1->left),height(t1->right))+1;
  return t1;
}

//LR旋转，左双旋，虽然我也没明白为啥LR.
tree LR(tree t){
  t->left = RR(t->left);
  return LL(t);
}

//RL旋转
tree RL(tree t){
   t->right = LL(t->right);
  return RR(t);
}

/*比较难一点的插入操作*/
tree insert(tree t,int val){
  if(t==NULL){//插入到叶节点上。
    t = new avl;
    t->val = val;
    t->left = t->right = NULL;
    t->h = 0;
    return t;
  }
  if(val > t->val){//走右边
    t->right = insert(t->right,val);
    if(height(t->right)-height(t->left)==2){//判断是否
//违反高度平衡条件。
      if(val > t->right->val){//如果走的子树右边
        t = RR(t);
      }
      else{//走的子树左边
        t = RL(t);
      }
    }
  }
  else{
    t->left = insert(t->left,val);
 //判断平衡条件
    if(height(t->left)-height(t->right)==2){
      if(val < t->left->val){
        t = LL(t);
      }
      else{
        t = LR(t);
      }
    }
  }
  t->h = max(height(t->left),height(t->right))+1;
  return t;
}
/*寻找最大值*/
tree findMax(tree t){
  while(t->right)t=t->right;
  return t;
}
/*永远都最难的删除。*/
tree del(tree t,int val){
//首先找到需删除的节点。
  tree v;
  if(t==NULL)return NULL;//为空说明没找到该值。
  if(val > t->val){//往右走。
    t->right = del(t->right,val);
    //删除可能会破坏平衡条件，调整，往右走，右子树可能变低。
    if(height(t->left) - height(t->right) == 2){
      if(height(t->left->left) >= height(t->left->right)){
        t = LL(t);
      }
      else{ t = LR(t);}
    }
  }
  else if(val < t->val){
    t->left = del(t->left,val);
    //左子树可能变低。
    if(height(t->right) - height(t->left) == 2){
      if(height(t->right->right) >= height(t->right->left)){
        t = RR(t);
      }
      else{ t = RL(t);}
    }
  }
  else{
    if(t->left == NULL){//只有一个儿子时，可以直接把另一个儿子接上来。
      v = t->right;delete t;
      return v;
    }
    else if(t->right == NULL){
      v = t->left;delete t;
      return v;
    }
    else{//双儿子时，查找左子树最大值。
      v = findMax(t->left);
      if(v == t->left){//刚好是左儿子，直接把左儿子右子树接上来。
        t->left = v->left;
        t->val = v->val;
        delete v;//调整高度。
        t->h = max(height(t->left),height(t->right))+1;
      }
      else{//否则删除把最大值赋值给t，递归删除最大值，因为此时
      //最大值必定没有右儿子。
        t->val = v->val;
        del(t->left,v->val);
      }
    }
  }
  return t;
}
void travel(tree t){
  if(!t)return;
  if(t->left)travel(t->left);
  cout << t->val << " ";
  if(t->right)travel(t->right);
}
void level(tree t){
  if(!t)return;
  tree now,last=t;
  queue<tree> qu;
  qu.push(t);
  while(qu.size()){
    now = qu.front();qu.pop();
    if(now->left)qu.push(now->left);
    if(now->right)qu.push(now->right);
    cout << now->val << "(" << now->h << ")" << " ";
    if(now == last && qu.size()){last = qu.back();cout << endl;}
  }
  cout << endl;
}
int main(){
  int a[10] = {1,8,3,0,9,5,6,2,4,7};
  tree t = NULL;
  int i;
  for(i=0;i<10;i++){
    t = insert(t,a[i]);
  }
  travel(t);cout << endl;
  level(t);
  t = del(t,8);
  travel(t);cout << endl;
  level(t);
}



二、优化版本的avl树。

  这个思路是网上看到的，其实我也一直再想因为左旋右旋操作是对称的，能不能写成一个函数。偶然还真看到了这种实现，记录下来。

 主要思路是使用一个布尔值来表示左右子树，0代表左，1代表右。

  

#include<iostream>
#include<queue>
using namespace std;

struct avl{
  avl* child[2];
  int val,h;//val值域，h高度。
  avl(int v,int hei):val(v),h(hei){child[0] = child[1] = NULL;}
};
typedef avl* tree;
int height(tree t){
  if(t==NULL)return -1;
  else{return t->h;}
}
/*旋转操作不会改变二叉搜索树的有序性，即左<中<右。
它只会调整左右子树的高度差，高的降低，低的提高。*/
//单旋
tree SR(tree t,bool c){
  tree t1 = t->child[c];
  t->child[c] = t1->child[!c];
  t1->child[!c] = t;
//调整后t,t1的高度都会改变，但是t的子树高度未变，先
//调整它。
  t->h = max(height(t->child[c]),height(t->child[!c]))+1;
//再调整t1
  t1->h = max(height(t1->child[c]),height(t1->child[!c]))+1;
  return t1;
}

//双旋
tree DR(tree t,bool c){
  t->child[c] = SR(t->child[c],!c);
  return SR(t,c);
}

/*比较难一点的插入操作*/
tree insert(tree t,int val){
  if(t==NULL){//插入到叶节点上。
    t = new avl(val,0);
    return t;
  }
  bool c=0;
  if(val>t->val)c=1;
  t->child[c] = insert(t->child[c],val);
  if(height(t->child[c])-height(t->child[!c])==2){//判断是否
//违反高度平衡条件。
    if( (val < t->child[c]->val) ^ c){t = SR(t,c);}
    else{t = DR(t,c);}
  }
  t->h = max(height(t->child[0]),height(t->child[1]))+1;
  return t;
}
/*寻找最大值*/
tree findMax(tree t){
  while(t->child[1])t=t->child[1];
  return t;
}
/*永远都最难的删除。*/
tree del(tree t,int val){
//首先找到需删除的节点。
  tree v;
  if(t==NULL)return NULL;//为空说明没找到该值。
  bool c=0;
  if(val != t->val){
    if(val > t->val)c = 1;
    t->child[c] = del(t->child[c],val);
    if(height(t->child[!c]) - height(t->child[c]) == 2){
      if(height(t->child[!c]->child[!c]) >= height(t->child[!c]->child[c])){t = SR(t,c);}
      else{ t = DR(t,c);}
    }
  }
  else{
    if(t->child[0] && t->child[1]){//双儿子时，查找左子树最大值。
      v = findMax(t->child[0]);
      if(v == t->child[0]){//刚好是左儿子，直接把左儿子右子树接上来。
        t->child[0] = v->child[1];
        t->val = v->val;
        delete v;//调整高度。
        t->h = max(height(t->child[0]),height(t->child[1]))+1;
      }
      else{//否则删除把最大值赋值给t，递归删除最大值，因为此时
      //最大值必定没有右儿子。
        t->val = v->val;
        del(t->child[0],v->val);
      }
    }
   else{
     if(t->child[1])c=1;
     v = t->child[c];
     delete t;
     return v;
   }
 }
  return t;
}
void travel(tree t){
  if(!t)return;
  if(t->child[0])travel(t->child[0]);
  cout << t->val << " ";
  if(t->child[1])travel(t->child[1]);
}
void level(tree t){
  if(!t)return;
  tree now,last=t;
  queue<tree> qu;
  qu.push(t);
  while(qu.size()){
    now = qu.front();qu.pop();
    if(now->child[0])qu.push(now->child[0]);
    if(now->child[1])qu.push(now->child[1]);
    cout << now->val << "(" << now->h << ")" << " ";
    if(now == last && qu.size()){last = qu.back();cout << endl;}
  }
  cout << endl;
}
int main(){
  int a[10] = {1,8,3,0,9,5,6,2,4,7};
  tree t = NULL;
  int i;
  for(i=0;i<10;i++){
    level(t);
    t = insert(t,a[i]);
  }
  travel(t);cout << endl;
  level(t);
  t = del(t,8);
  travel(t);cout << endl;
  level(t);
}


LifeIsStudy
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
二叉树的应用：二叉排序树BST和平衡二叉树AVL的构造 课设作业 完整代码
02-10
平衡二叉树（Balanced Binary Tree）又被称为AVL树。具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。构造与调整方法。 实验目的： 二叉排序树的实现...
【数据结构】这些二叉树经典面试题帮你快速入门二叉树
Living_Amethyst的博客
06-27 1248
二叉树入门到精通
有关二叉排序树的代码实现
yangshuolll的专栏
10-19 281
参考文章一 参考文章二 #include #include #include #include using namespace std; struct biTree{ int data; biTree *left; biTree *right; }; //插入数据 biTree* insertEle(biTree *t, int key){ if (t == NUL
二叉树的简单操作（C语言实现）
gangber的博客
10-15 139
//bintree.h #ifndef _BINTREE_H_ #define _BINTREE_H_ #include<stdio.h> #include<stdlib.h> #include<windows.h> #include<assert.h> #pragma warning(disable:4996) typedef char ElemType; typedef struct BintreeNode { ElemType val; st
数据结构：平衡二叉树（AVL树）
weixin_30542079的博客
01-10 72
AVL树是每个结点的左子树和右子树的高度最多差1的二叉查找树。 要维持这个树，必须在插入和删除的时候都检测是否出现破坏树结构的情况。然后立刻进行调整。 看了好久，网上各种各种的AVL树，千奇百怪。 关键是要理解插入的时候旋转的概念。 // // AvlTree.h // HelloWorld // csdn blog：http://blog.csdn.net/u0121750...
数据结构之 平衡二叉树总结
徐小航航 的博客
08-09 570
   敲这个题时，预备知识是知道四种旋转方式，分别是LL、RR、LR、RL，对应每一种的变换方式要做到会旋转，会写关键的代码 这个题是参照一篇博客写的，然后自己又理解了一遍。 #include &lt;stdio.h&gt; #include &lt;stdlib.h&gt; #include &lt;string.h&gt; struct node { struct node...
avl_tree:AVL树的python实现（自平衡二叉树）
07-02
avl_tree AVL树的python实现（自平衡二叉树） 描述： 这是具有以下外部方法的平衡二叉搜索树的实现： insert (data) 将数据插入树中，如果它尚未包含在树中insertList (list)通过迭代调用insert将list中的数据元素...
C语言数据结构之平衡二叉树（AVL树）实现方法示例
08-28
主要介绍了C语言数据结构之平衡二叉树（AVL树）实现方法,结合实例形式分析了C语言平衡二叉树的相关定义与使用技巧,需要的朋友可以参考下
平衡二叉树-AVL树的实现
12-10
首先实现BST二叉搜索树，在BST的基础上做出AVL树，有插入、删除、查询、调整平衡的功能，而且可以和BST比较的过程。By Michael Zhou
AVLtree_c_avl_平衡二叉树_avltree_
10-02
将平衡二叉树的增删改查集成到了一起，提供友好的界面。
平衡二叉树总结
zxzxin的博客~
04-20 3783
目录 平衡二叉树相关概念以及性质 平衡二叉树的类结构 LL型失衡以及解决办法 RR型失衡以及解决办法 LR型失衡以及解决办法 RL型失衡以及解决办法 balance和checkBalance函数 完整源码测试 说明 在学二叉平衡树之前，可以先学一下二叉排序树。 在下面的源代码中，设计的二叉查找树的insert方法和remove方法，以及findMin()和findMa...
查找算法总结(4)--平衡二叉树
liqiutuoyuan的博客
05-30 1327
平衡二叉树
平衡二叉树详解
weixin_43899008的博客
03-27 9068
一、平衡二叉树 平衡二叉搜索树又被称为AVL树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL等。 二、作用 我们有时在编程过程中可能会需要用到链表（时间复杂度O(n)）来进行对数据的存储，但是当数据量变得十分庞大时我们对于指定数据的一些操作的时间消耗就会变得大，这时我们就需要借助将链表的结构变为二叉搜索树（时间复杂度O(logn)）来进行数据的存储。 但在某些情况下，例如：对[1,2,3,4,5,6,…]
AVL平衡二叉树总结
iQXQZX
12-19 329
我个人是通过b站学习的懂得 b站视频连接： https://www.bilibili.com/video/av37955102?from=search&amp;seid=14638889623357631324 https://www.bilibili.com/video/av37955178?from=search&amp;seid=14638889623357631324 https:...
平衡二叉树总结一：二叉搜索树
tdscdma123的博客
01-03 400
这段时间一直再刷leetcode，现在刷了快一半了吧，感觉没什么状态了，再继续刷可能就不太好了，想想不如回头再补补算法吧。总结了自己在基础算法上的一些短板，准备后面这些时间把它们都补上。好了，上正题。   平衡二叉树算是应用最广泛的树型结构了吧，至少在内存里面是吧。刚开始学数据结构的时候，树的那一章基本没怎么看，大部分精力都放在了排序和图论里，而且感觉树也挺简单的，现在刷题才慢慢发现这种数据结构
二叉树各种操作的总结
quinn的专栏
07-26 5675
求二叉树中的节点个数 求二叉树中叶子节点的个数 求二叉树的深度 求二叉树第K层的节点个数 递归遍历前序中序后序 非递归遍历前序中序后序层序 1 前序遍历 2 中序遍历 3 后序遍历 4 层序遍历 将二叉查找树变为有序的双向链表 判断两棵二叉树是否结构相同 判断二叉树是不是平衡二叉树 判断二叉树是否是搜索二叉树 求二叉树中两个节点的最低公共祖先节点 求二叉树中节点的最大距离 由前序遍历序列和中序遍历序列重建二叉树
平衡二叉树（AVL）知识点总结
陈实Yepper
12-04 506
1、平衡二叉树的基本概念 平衡二叉树构建的基本思想是在构建二叉搜索树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。 最小不平衡子树：距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树。 在保持二叉搜索树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。 二叉搜索树，又称二叉排序树，二叉查找树...
随机化的二叉搜索树总结（treap,随机输入）
tdscdma123的博客
01-06 2032
看数据结构的时候，书里面说对于随机输入的序列，BST的期望深度是log(n),当时没当一回事（其实是证明看不懂），这两天复习二叉搜索树遇到树堆（treap）又回去翻了一下证明过程，其实还蛮简单的。    总结起来也就一句话：    只要保证BST的任意子树的根节点选取是随机的，那么这颗树的期望深度就必然是log(n). 证明如下：  1.首先要定义一个概念——内部路径长（D（N）），也就是
平衡二叉树（AVL树） 删除结点
最新发布
05-22
在平衡二叉树（AVL树）中删除结点，需要先找到要删除的结点，然后将其替换为其前驱或后继结点。然后，我们需要对替换结点的父节点和祖先节点进行旋转操作，以维护平衡性。 具体的删除步骤如下： 1. 找到要删除的...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值