平衡二叉树总结一：二叉搜索树

  这段时间一直再刷leetcode，现在刷了快一半了吧，感觉没什么状态了，再继续刷可能就不太好了，想想不如回头再补补算法吧。总结了自己在基础算法上的一些短板，准备后面这些时间把它们都补上。好了，上正题。

  平衡二叉树算是应用最广泛的树型结构了吧，至少在内存里面是吧。刚开始学数据结构的时候，树的那一章基本没怎么看，大部分精力都放在了排序和图论里，而且感觉树也挺简单的，现在刷题才慢慢发现这种数据结构的威力，虽然c++的算法库已经有了现成的工具，但是学习好这种数据结构的思想还是很有必要的。

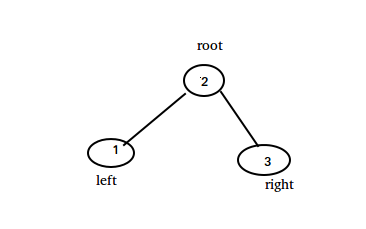
  首先，平衡二叉树是一颗二叉搜索树。其结构满足 root->left->val < root-> val < root->right->val 即根节点左儿子值 < 根节点值 < 右儿子值，并且根节点左右儿子也是二叉搜索树。

第一次作图，凑或着看吧

struct searchTree{
  searchTree* left;
  searchTree* right;
  int val;
}
typedef serachTree* tree;
二叉搜索树的结构，c++版。主要是一个左指针、一个右指针、一个值，不难看出left与right其实是“多余”的，然而没有这俩多余的域二叉树的搜索效率就无从谈起，这就是空间
换时间的典型吧。

  1.二叉搜索树的搜索

  二叉搜索树操作都很简单，搜索时，我们只需比较待搜索值与根节