下面来详细讲一下如何用回溯算法来解数独问题。
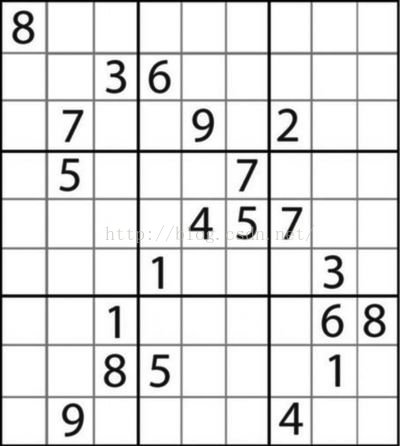
下图是一个数独题,也是号称世界上最难的数独。当然了,对于计算机程序来说,只要算法是对的,难不难就不知道了,反正计算机又不累。回溯算法基本上就是穷举,解这种数独类的问题逻辑比较简单。
不管算法懂不懂,先把类建出来,变量定义好,那放大学试卷上就是可以拿两分了。
package shudu;
/**
* Created by wolf on 2016/3/17.
*/
public class Sudoku {
private int[][] matrix;
public Sudoku(int[][] matrix) {
this.matrix = matrix;
}
public static void main(String[] args) {
// 号称世界上最难数独
int[][] sudoku = {
{8, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 3, 6, 0, 0, 0, 0, 0},
{0, 7, 0, 0, 9, 0, 2, 0, 0},
{0, 5, 0, 0, 0, 7, 0, 0, 0},
{0, 0, 0, 0, 4, 5, 7, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 3, 0},
{0, 0, 1, 0, 0, 0, 0, 6, 8},
{0, 0, 8, 5, 0, 0, 0, 1, 0},
{0, 9, 0, 0, 0, 0, 4, 0, 0}};
Sudoku s = new Sudoku(sudoku);
s.backTrace(0, 0);
}
/**
* 数独算法
* @param i
* 行号
* @param j
* 列号
*/
private void backTrace(int i, int j) {
}
}
用一个二维数组来存储这个矩阵,然后定义一个方法来计算。方法里有两个属性——行号和列号。
我们的原理就是从第0行0列开始,依次往里面填入1-9之间的数字,然后判断填入的这个数字是否能放进去(该行该列和它所在的小九宫格是否有重复数字)。如果能放进去,那么就继续用1-9去试该行的下一列。一直到该行的最后一列,然后换行继续重复上面的步骤(也就是执行backTrace方法)。一直执行到最后一个空格,也就是i=8,j=8的时候,且最后这个空格所放的值也完全符合规则,那么此时就算完成,不用再继续调用backTrace方法了,输出正确解即可。
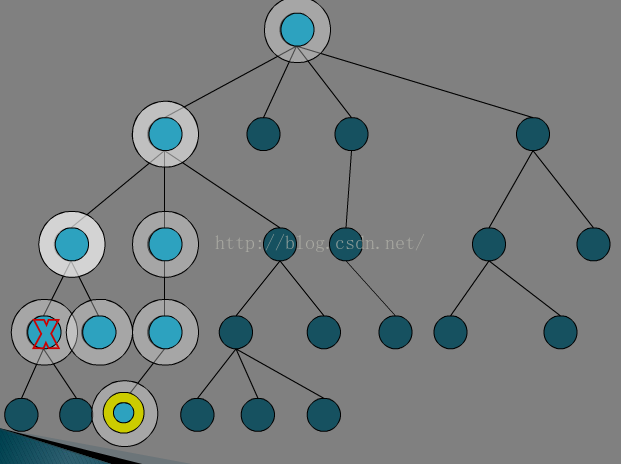
所以回溯法样子看起来是这样的。给第一个空格填1-9中任何一个,开始判断,如果OK,然后进入下一层,如果不OK,就断掉了。下一层还是从1-9开始试,然后OK,不OK……当最终目标达到时,空格已填满又满足条件,那么中断该分支,输出结果。
继续我们的程序。
由于有些位置已经有数字了,所以我们需要判断,如果该坑已经有人蹲了,那么就把列号j加1,进入下一列。如果到第8列了,就换行。
修改程序如下:
package shudu;
/**
* Created by wolf on 2016/3/17.
*/
public class Sudoku {
private int[][] matrix;
public Sudoku(int[][] matrix) {
this.matrix = matrix;
}
public static void main(String[] args) {
// 号称世界上最难数独
int[][] sudoku = {
{8, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 3, 6, 0, 0, 0, 0, 0},
{0, 7, 0, 0, 9, 0, 2, 0, 0},
{0, 5, 0, 0, 0, 7, 0, 0, 0},
{0, 0, 0, 0, 4, 5, 7, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 3, 0},
{0, 0, 1, 0, 0, 0, 0, 6, 8},
{0, 0, 8, 5, 0, 0, 0, 1, 0},
{0, 9, 0, 0, 0, 0, 4, 0, 0}};
Sudoku s = new Sudoku(sudoku);
s.backTrace(0, 0);
}
/**
* 数独算法
*
* @param i 行号
* @param j 列号
*/
private void backTrace(int i, int j) {
//如果i行j列是空格,那么才进入给空格填值的逻辑
if (matrix[i][j] == 0) {
for (int k = 1; k <= 9; k++) {
//判断给i行j列放1-9中的任意一个数是否能满足规则
if (check(i, j, k)) {
//将该值赋给该空格,然后进入下一个空格
matrix[i][j] = k;
backTrace(i, j + 1);
}
}
} else {
//如果该位置已经有值了,就进入下一个空格进行计算
backTrace(i, j + 1);
}
}
/**
* 判断给某行某列赋值是否符合规则
*
* @param row 被赋值的行号
* @param line 被赋值的列号
* @param number 赋的值
* @return
*/
private boolean check(int row, int line, int number) {
//判断该行该列是否有重复数字
for (int i = 0; i < 9; i++) {
if (matrix[row][i] == number || matrix[i][line] == number) {
return false;
}
}
//判断小九宫格是否有重复
int tempRow = row / 3;
int tempLine = line / 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (matrix[tempRow * 3 + i][tempLine * 3 + j] == number) {
return false;
}
}
}
return true;
}
}
还缺少的是边界值的判断,就是当已经到最后一列了,还没到最后一行时,需要对行号加1,然后恢复列号为0。
修改一下backTrace方法,增加边界值判断。
package shudu;
/**
* Created by wolf on 2016/3/17.
*/
public class Sudoku {
private int[][] matrix;
public Sudoku(int[][] matrix) {
this.matrix = matrix;
}
public static void main(String[] args) {
// 号称世界上最难数独
int[][] sudoku = {
{8, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 3, 6, 0, 0, 0, 0, 0},
{0, 7, 0, 0, 9, 0, 2, 0, 0},
{0, 5, 0, 0, 0, 7, 0, 0, 0},
{0, 0, 0, 0, 4, 5, 7, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 3, 0},
{0, 0, 1, 0, 0, 0, 0, 6, 8},
{0, 0, 8, 5, 0, 0, 0, 1, 0},
{0, 9, 0, 0, 0, 0, 4, 0, 0}};
Sudoku s = new Sudoku(sudoku);
s.backTrace(0, 0);
}
/**
* 数独算法
*
* @param i 行号
* @param j 列号
*/
private void backTrace(int i, int j) {
if (i == 8 && j == 9) {
//已经成功了,打印数组即可
System.out.println("获取正确解");
printArray();
return;
}
//已经到了列末尾了,还没到行尾,就换行
if (j == 9) {
i++;
j = 0;
}
//如果i行j列是空格,那么才进入给空格填值的逻辑
if (matrix[i][j] == 0) {
for (int k = 1; k <= 9; k++) {
//判断给i行j列放1-9中的任意一个数是否能满足规则
if (check(i, j, k)) {
//将该值赋给该空格,然后进入下一个空格
matrix[i][j] = k;
backTrace(i, j + 1);
}
}
} else {
//如果该位置已经有值了,就进入下一个空格进行计算
backTrace(i, j + 1);
}
}
/**
* 判断给某行某列赋值是否符合规则
*
* @param row 被赋值的行号
* @param line 被赋值的列号
* @param number 赋的值
* @return
*/
private boolean check(int row, int line, int number) {
//判断该行该列是否有重复数字
for (int i = 0; i < 9; i++) {
if (matrix[row][i] == number || matrix[i][line] == number) {
return false;
}
}
//判断小九宫格是否有重复
int tempRow = row / 3;
int tempLine = line / 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (matrix[tempRow * 3 + i][tempLine * 3 + j] == number) {
return false;
}
}
}
return true;
}
/**
* 打印矩阵
*/
public void printArray() {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
System.out.println();
}
}
可以看到,判断成功的标志是行号为8,且列号为9时,认为找到了正确解。为什么是9呢,因为在check(i,j,k)那一步,通过了的话,将值K赋给最后一个空格,此时并没有中断程序,而且进入了下一层循环backTrace(i,j + 1),所以i为8j为9时才是终解。程序到这里,运行一下看看,发现并没有任何输出值,并没有找到正确解,why?
下面要讲的就是该程序最关键的地方,也是比较难以理解的地方,就是对根节点的初始化。回溯算法讲究的是一条道走到黑,不撞南墙不回头,并且把所有的道都走完。
我们把问题简单化,譬如一共只有两个空格,只能放0和1,正确答案是00和11.我们给第一个空格放了0,此时我们不知道是否放了0之后,后面是否能完全正确的走完全程。就像走迷宫一样,你选择了第一个岔道,此时有可能第一个岔道就是错的,后面无论怎么走都对了不了,也有可能有多条道可以走。那么我们的做法是先第一步放0,发现没问题(符合只能放0和1的规则),然后走第二步,第二步如果走对了,那就直接走出去了,获得了一次正确的解(00)。如果第二步是个死胡同(01),那就要回头了,就是要回到原点,把第一步初始化一下,然后第一步走1,然后再继续后面的步骤。所以无论怎么样,你都需要在第二步走完之后,把第一步走的值给清掉,回归到原点。这样才能找到所有的正确路线。
问题放大一下,有N步(N未知),第一步有1-9共9种情况,第一步放了1,后面还有未知的步,那无论后面成功与否,你肯定都要去试第一步放2-9之间的数字。
看第51行for循环那里,第一次将数字1赋给第一个空格。然后判断是否OK,如果OK了,就进入第二个空格去了,后面具体走多少步我们就不管了,我们只需要在后面的走完之后,初始化第一个空格就行了。那要是不OK呢,不OK当然就不用管他了,这一层走完就没下文了,等于该分支就断了。所以我们要在第55行后面加一句初始化的操作matrix[i][j]=0.
完整代码如下:
package shudu;
/**
* Created by wolf on 2016/3/17.
*/
public class Sudoku {
private int[][] matrix;
public Sudoku(int[][] matrix) {
this.matrix = matrix;
}
public static void main(String[] args) {
// 号称世界上最难数独
int[][] sudoku = {
{8, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 3, 6, 0, 0, 0, 0, 0},
{0, 7, 0, 0, 9, 0, 2, 0, 0},
{0, 5, 0, 0, 0, 7, 0, 0, 0},
{0, 0, 0, 0, 4, 5, 7, 0, 0},
{0, 0, 0, 1, 0, 0, 0, 3, 0},
{0, 0, 1, 0, 0, 0, 0, 6, 8},
{0, 0, 8, 5, 0, 0, 0, 1, 0},
{0, 9, 0, 0, 0, 0, 4, 0, 0}};
Sudoku s = new Sudoku(sudoku);
s.backTrace(0, 0);
}
/**
* 数独算法
*
* @param i 行号
* @param j 列号
*/
private void backTrace(int i, int j) {
if (i == 8 && j == 9) {
//已经成功了,打印数组即可
System.out.println("获取正确解");
printArray();
return;
}
//已经到了列末尾了,还没到行尾,就换行
if (j == 9) {
i++;
j = 0;
}
//如果i行j列是空格,那么才进入给空格填值的逻辑
if (matrix[i][j] == 0) {
for (int k = 1; k <= 9; k++) {
//判断给i行j列放1-9中的任意一个数是否能满足规则
if (check(i, j, k)) {
//将该值赋给该空格,然后进入下一个空格
matrix[i][j] = k;
backTrace(i, j + 1);
//初始化该空格
matrix[i][j] = 0;
}
}
} else {
//如果该位置已经有值了,就进入下一个空格进行计算
backTrace(i, j + 1);
}
}
/**
* 判断给某行某列赋值是否符合规则
*
* @param row 被赋值的行号
* @param line 被赋值的列号
* @param number 赋的值
* @return
*/
private boolean check(int row, int line, int number) {
//判断该行该列是否有重复数字
for (int i = 0; i < 9; i++) {
if (matrix[row][i] == number || matrix[i][line] == number) {
return false;
}
}
//判断小九宫格是否有重复
int tempRow = row / 3;
int tempLine = line / 3;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (matrix[tempRow * 3 + i][tempLine * 3 + j] == number) {
return false;
}
}
}
return true;
}
/**
* 打印矩阵
*/
public void printArray() {
for (int i = 0; i < 9; i++) {
for (int j = 0; j < 9; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
System.out.println();
}
}
 回溯法解数独
回溯法解数独







 本文详细介绍使用回溯算法解决数独问题的过程。通过逐步解析并实现算法,演示如何检查每一步填充数字是否符合数独规则,最终找到所有可能的解。
本文详细介绍使用回溯算法解决数独问题的过程。通过逐步解析并实现算法,演示如何检查每一步填充数字是否符合数独规则,最终找到所有可能的解。

















 3707
3707

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










