CCF201409-2 画图（100分）

试题编号：	201409-2
试题名称：	画图
时间限制：	1.0s
内存限制：	256.0MB
问题描述：	问题描述 　　在一个定义了直角坐标系的纸上，画一个(x1,y1)到(x2,y2)的矩形指将横坐标范围从x1到x2，纵坐标范围从y1到y2之间的区域涂上颜色。 　　下图给出了一个画了两个矩形的例子。第一个矩形是(1,1) 到(4, 4)，用绿色和紫色表示。第二个矩形是(2, 3)到(6, 5)，用蓝色和紫色表示。图中，一共有15个单位的面积被涂上颜色，其中紫色部分被涂了两次，但在计算面积时只计算一次。在实际的涂色过程中，所有的矩形都涂成统一的颜色，图中显示不同颜色仅为说明方便。 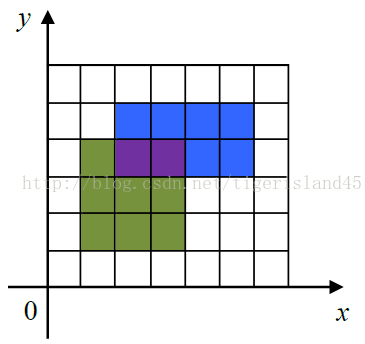　　给出所有要画的矩形，请问总共有多少个单位的面积被涂上颜色。 输入格式 　　输入的第一行包含一个整数n，表示要画的矩形的个数。 　　接下来n行，每行4个非负整数，分别表示要画的矩形的左下角的横坐标与纵坐标，以及右上角的横坐标与纵坐标。 输出格式 　　输出一个整数，表示有多少个单位的面积被涂上颜色。 样例输入 2 1 1 4 4 2 3 6 5 样例输出 15 评测用例规模与约定 　　1<=n<=100，0<=横坐标、纵坐标<=100。

问题链接：CCF201409试题。

问题描述：

  输入n个矩形的左下角的横坐标与纵坐标，以及右上角的横坐标与纵坐标，求这些矩形所覆盖的面积。

问题分析：

  若干个矩形叠加在一起，要算出其面积，看起来有点复杂。关键是其面积是由若干正方形组成的。计算的方法有两种：

  1.将各个正方形标记出来，然后再统计计算其面积。

  2.将各个正方形面积累加起来，然后去掉重叠部分。哪些部分重叠也需要进行标记后才能判定。

程序说明：

  本程序采用第2种方法进行计算。

提交后得100分的C++语言程序如下：

/* CCF201409-2 画图 */

#include <iostream>
#include <cstring>

using namespace std;

const int N = 100;

bool flag[N+1][N+1];

int main()
{
    int n, x1, y1, x2, y2, sum=0;

    // 变量初始化
    memset(flag, false, sizeof(flag));

    // 输入数据，计算处理
    cin >> n;
    for(int i=1; i<=n; i++) {
        // 输入数据
        cin >> x1 >> y1 >> x2 >> y2;

        // 累加面积
        sum += (x2 - x1) * (y2 - y1);

        // 标记和去除重叠部分
        for(int i=x1; i<x2; i++)
            for(int j=y1; j<y2; j++) {
                if(flag[i][j])
                    sum--;
                flag[i][j] = true;
            }
    }

    // 输出结果
    cout << sum << endl;

    return 0;
}