线段树的查询
题目
对于一个有n个数的整数数组,在对应的线段树中, 根节点所代表的区间为0-n-1, 每个节点有一个额外的属性max,值为该节点所代表的数组区间start到end内的最大值。
为SegmentTree设计一个 query 的方法,接受3个参数root, start和end,线段树root所代表的数组中子区间[start, end]内的最大值。注意事项
在做此题之前,请先完成 线段树构造 这道题目。样例
对于数组 [1, 4, 2, 3], 对应的线段树为:
query(root, 1, 1), return 4
query(root, 1, 2), return 4
query(root, 2, 3), return 3
query(root, 0, 2), return 4题解
以[start,end]与[root.start,root.end]的中间点mid的位置关系为关键点,分情况计算。如mid位于[start,end]中间则需要同时考虑左右两边的数据,否则表明[start,end]只位于root的左子树或者右子树,继续递归即可。
/**
* Definition of SegmentTreeNode:
* public class SegmentTreeNode {
* public int start, end, max;
* public SegmentTreeNode left, right;
* public SegmentTreeNode(int start, int end, int max) {
* this.start = start;
* this.end = end;
* this.max = max
* this.left = this.right = null;
* }
* }
*/
public class Solution {
/**
*@param root, start, end: The root of segment tree and
* an segment / interval
*@return: The maximum number in the interval [start, end]
*/
public int query(SegmentTreeNode root, int start, int end) {
if (root.start == start && root.end == end)
{
return root.max;
}
int leftMax = Integer.MIN_VALUE;
int rightMax = Integer.MIN_VALUE;
int mid = (root.start + root.end) / 2;
if (start <= mid)
{
leftMax = query(root.left,start,Math.min(mid,end));
}
if (mid < end)
{
rightMax = query(root.right,start <= mid ? ++mid : start,end);
}
return Math.max(leftMax,rightMax);
}
}Last Update 2016.11.3








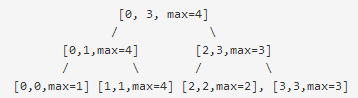















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








