POJ2676Sudoku(AC2)

Sudoku

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 16420		Accepted: 8020		Special Judge

Description

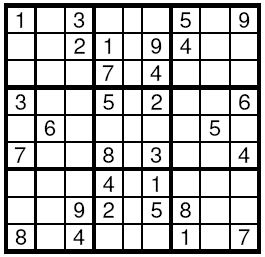
Sudoku is a very simple task. A square table with 9 rows and 9 columns is divided to 9 smaller squares 3x3 as shown on the Figure. In some of the cells are written decimal digits from 1 to 9. The other cells are empty. The goal is to fill the empty cells with decimal digits from 1 to 9, one digit per cell, in such way that in each row, in each column and in each marked 3x3 subsquare, all the digits from 1 to 9 to appear. Write a program to solve a given Sudoku-task.

Input

The input data will start with the number of the test cases. For each test case, 9 lines follow, corresponding to the rows of the table. On each line a string of exactly 9 decimal digits is given, corresponding to the cells in this line. If a cell is empty it is represented by 0.

Output

For each test case your program should print the solution in the same format as the input data. The empty cells have to be filled according to the rules. If solutions is not unique, then the program may print any one of them.

Sample Input

1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127

 
 
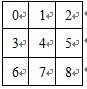
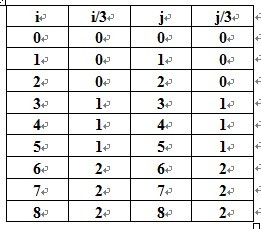
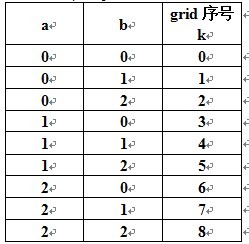
这个是从小优博客copy的，小优博客版权所有
首先我们假设子网格的序号如下编排：
由于1<=i、j<=9，我们有： （其中“/”是C++中对整数的除法）
令a= i/3 , b= j/3  ，根据九宫格的 行列 与 子网格 的 关系，我们有:
 
 
<pre class="cpp" name="code">//这道题刚开始不知道用什么方法，用dfs又怕超时，后来百度还是确认用dfs,汗，还是要提高个人能力啊
#define _CRT_SECURE_NO_WARNINGS

/*第一次提交WA，答案确实有错。。。没有初始化，因为后面几个visit变量是看百度设的，之前init函数又没加，导致出错*/

#if 1

#include <stdio.h>

#define MANINT 10 //9*9
char map[MANINT][MANINT]; //因为没有空格的，所以
int  sudo[MANINT][MANINT]; //int的输入
int  visit[MANINT][MANINT];//哪些格子已经填好
int  cannotmodify[MANINT][MANINT]; //哪些点是不可以更改的，一开始数字就给好了

/*除了上面还要加三个标记，这个是看了小优博客才这么想的，其实自己也能想到，就是不自信啊。。。不要怕写无用的代码*/
/*然后自己又犯了个本质的错误就是dfs刚开始用的void型。。。还是要用int型，有返回值的,想想也是，没返回值那成功了怎么返回呢？看了
只有像sky map那种不用返回值，回溯类型的都需要返回值的*/
int visitrow[MANINT][MANINT]; //visitrow[1][9]表示第一行9已经用了
int visitclum[MANINT][MANINT];//visitclum[1][9]表示第一列9已经用了
int visitminimatrix[MANINT][MANINT];//visitminimatrix[1][9]表示在第1个3*3子格中9已经用了

int dir[4][2] = { { 1, 0 }, { -1, 0 }, { 0, 1 }, { 0, -1 } };

//想来想去，觉得很是复杂，最后还是参考小优博客http://blog.csdn.net/lyy289065406/article/details/6647977
//还有是这个赋值都是给没有填数的赋，这个自己写的也是对的，对有初始值的都做了标记了
/*有4个条件
   1:一行中的数字不能重复，
   2：一列的数字不能重复，
   3:3*3的小格子不能重复 -----这个怎么判断？
   4:数字1~9*/

//自己一直做不对的原因在于如果这个格子有数要调用dfs的时候也是要回溯的，但是自己没有回溯


int num = 0;

//用dfs做这道题
//是不是还要3*3的做？有好多结果啊
int dfs(int x, int y)
{
	int i = 0;
	int j = 0;
	int x1 = 0;
	int y1 = 0;
	if (9 == y) return 1;
	//if (x <0 || x>=9||y<0||y>=9) return 0;
	if (81 == num) return 1;   //81个点都设置好了值

	//要根据x,y算出这个格子属于哪个子格
	int k = 3 * (x / 3) + y / 3;//这个公式不是自己推的

	//这边写可以填的数字，我原来是从4个方向dfs填格子，不知道对不对，这样的话就不能
	//用这4个方向的不行，这个不确定性太大了，要向turn over the game一样是个固定矩阵，那可以自己指定顺序，这样是不是更好些
	//for (i = 0; i < 4;i++)
	//{ //自己用4个方向找的,就一直出不来
	if (8 == x)  
	{
		x1 = 0; //自己原来写的1不对，x是从0开始的
		y1 = y + 1;
	}
	else
	{
		x1 = x + 1;
		y1 = y;
	}


	if (0 != sudo[x][y])
	{
		//直接找下一个点
		//这边也要回溯的啊。。。这边自己刚开始写的时候没写回溯，直接就调用了个dfs(x1, y1)
		if (1 == dfs(x1, y1))
		{
			return 1;
		}
		else
		{
			return 0;
		}
		
	}
	else
	{
		//找出这个格子可以选的数
		for (j = 1; j <= 9;j++)
		{
			if (1 == visitrow[x][j]) continue;
			if (1 == visitclum[y][j]) continue;
			if (1 == visitminimatrix[k][j]) continue;
			sudo[x][y]            = j;
			visit[x][y]           = 1;
			visitrow[x][j]         = 1;
			visitclum[y][j]        = 1;
			visitminimatrix[k][j]  = 1;
			num += 1;
			if (1 == dfs(x1, y1))
			{
				return 1;
			}
			else
			{
				//回溯
				sudo[x][y]            = 0;
				visit[x][y]           = 0;
				visitrow[x][j]        = 0;
				visitclum[y][j]       = 0;
				visitminimatrix[k][j] = 0;
				num -= 1;
			}
		}
	}
	return 0;
}

void init()
{
	int i = 0;
	int j = 0;
	for (i = 0; i < MANINT; i++)
	{
		for (j = 0; j < MANINT; j++)
		{
			map[i][j]            = '0';
			sudo[i][j]           = 0;
			visit[i][j]           = 0;
			cannotmodify[i][j]    = 0;
			visitrow[i][j]        = 0;
			visitclum[i][j]       = 0;
			visitminimatrix[i][j] = 0;
		}
	}
	num = 0;
	return;
}

int main()
{
	int i = 0;
	int j = 0;
	int T = 0;
	int k = 0;
	int flag = 0;
	freopen("input.txt","r",stdin);

	scanf("%d",&T);

	for (k = 0; k < T;k++)
	{
		init();
		//9*9的矩阵
		for (i = 0; i < 9; i++)
		{
			scanf("%s", &map[i]);
		}

		//转换成int型
		for (i = 0; i < 9; i++)
		{
			for (j = 0; j < 9; j++)
			{
				sudo[i][j] = map[i][j] - '0';
				if (0 != sudo[i][j])
				{
					int k = 3 * (i / 3) + j / 3;
					cannotmodify[i][j] = 1;
					visit[i][j] = 1;
					visitrow[i][sudo[i][j]] = 1;
					visitclum[j][sudo[i][j]] = 1;
					visitminimatrix[k][sudo[i][j]] = 1;
					num += 1;
				}
			}
		}

#if 0
		for (i = 0; i < 9; i++)
		{
			for (j = 0; j < 9; j++)
			{
				if (0 == sudo[i][j])
				{
					dfs(i, j); //这道题没什么对错，所以dfs()没有返回值  从第一个是0的开始dfs,错，如果这个格子放这个数不合适，那可能要回溯啊，要有返回值的

					//输出结果
					for (i = 0; i < 9; i++)
					{
						for (j = 0; j < 9; j++)
						{
							printf("%d", sudo[i][j]);
						}
						printf("\n");
					}
					flag = 1;
					break;
				}
			}
#endif
			dfs(0, 0); //这道题没什么对错，所以dfs()没有返回值  从第一个是0的开始dfs,错，如果这个格子放这个数不合适，那可能要回溯啊，要有返回值的

			//输出结果
			for (i = 0; i < 9; i++)
			{
				for (j = 0; j < 9; j++)
				{
					printf("%d", sudo[i][j]);
				}
				printf("\n");
			}
	}
	return 0;
}

#endif
 
 

//第2遍自己做的，独立完成，我觉得自己这个做法还是不错的，这个方块的分法自己也比较能明白
//poj2676sudu数独问题
//9*9分成了9个3*3的小块
//OK,自己做的，大概的印象还是有的主要就是在如果这个数是固定分配的return 1不能忘了也return 1，但是return 0的时候不能回溯
#include <stdio.h>
#define MAXINT 10
char mapchar[MAXINT][MAXINT];
int  mapint[MAXINT][MAXINT];
int mapafter[MAXINT][MAXINT];
int visithang[MAXINT][MAXINT];//visithang[1][2]第一行2已经被用了
int visitlie[MAXINT][MAXINT];//visitlie[1][2]第一列2已经被用了
int visitfangzhen[MAXINT][MAXINT];//visitfangzhen[1][2]第一个小方块2已经被用了



int getIndex(int x, int y)
{
	int index = 0;
	if ((x >= 1) && (x <= 3) && (y >= 1) && (y <= 3))
	{
		index = 1;
	}
	if ((x >= 1) && (x <= 3) && (y >= 4) && (y <= 6))
	{
		index = 2;
	}
	if ((x >= 1) && (x <= 3) && (y >= 7) && (y <= 9))
	{
		index = 3;
	}
	if ((x >= 4) && (x <= 6) && (y >= 1) && (y <= 3))
	{
		index = 4;
	}
	if ((x >= 4) && (x <= 6) && (y >= 4) && (y <= 6))
	{
		index = 5;
	}
	if ((x >= 4) && (x <= 6) && (y >= 7) && (y <= 9))
	{
		index = 6;
	}
	if ((x >= 7) && (x <= 9) && (y >= 1) && (y <= 3))
	{
		index = 7;
	}
	if ((x >= 7) && (x <= 9) && (y >= 4) && (y <= 6))
	{
		index = 8;
	}
	if ((x >= 7) && (x <= 9) && (y >= 7) && (y <= 9))
	{
		index = 9;
	}
	return index;
}


void init()
{
	int j = 0;
	int k = 0;
	for (j = 0; j < MAXINT; j++)
	{
		for (k = 0; k < MAXINT; k++)
		{
			mapchar[j][k]       = '0';
			mapint[j][k]        = 0;
			mapafter[j][k]      = 0;
			visithang[j][k]     = 0;
			visitlie[j][k]      = 0;
			visitfangzhen[j][k] = 0;
		}
	}
	return;
}

//逐列算
int dfs(int x,int y,int num)
{
	int i = 0;
	int fangzhen = 0;
	if (num == 81)
	{
		//printf("1\n");
		return 1;
	}

	if (y>9)
	{
		x = x + 1; //换下一行开始
		y = 1;
	}

	if (x>9) //检索完
	{
		//printf("2\n");
		return 1;
	}


	fangzhen = getIndex(x, y);

	if (0 != mapint[x][y])
	{
		if (1 == dfs(x, y + 1, num + 1))
		{
			return 1; //这边即使返回是0不能回溯，因为这边的分支的值是一开始就给好了，不能变，不不存在回溯
		}
	}
	else
	{
		for (i = 1; i <= 9;i++)
		{
			if (visithang[x][i]) continue;
			if (visitlie[y][i]) continue;
			if (visitfangzhen[fangzhen][i]) continue;
			visithang[x][i]       = 1;
			visitlie[y][i]        = 1;
			visitfangzhen[fangzhen][i] = 1;
			mapint[x][y]          = i;
			if (1 == dfs(x,y+1,num+1))
			{
				return 1;
			}
			else
			{
				//回溯
				visithang[x][i]        = 0;
				visitlie[y][i]         = 0;
				visitfangzhen[fangzhen][i] = 0;
				mapint[x][y]           = 0;
			}
		}
	}
	return 0;
}


int main()
{
	int i = 0;
	int j = 0;
	int k = 0;
	int T = 0;
	freopen("input.txt","r",stdin);
	scanf("%d",&T);
	for (i = 0; i < T;i++)
	{
		init();
		for (j = 1; j <= 9;j++)
		{
			scanf("%s",&mapchar[j]);
		}
		for (j = 1; j <= 9; j++)
		{
			for (k = 0; k < 9; k++)
			{
				mapint[j][k+1] = mapchar[j][k] - '0';
				if (0 != mapint[j][k + 1])
				{
					visithang[j][mapint[j][k + 1]] = 1;
					visitlie[k+1][mapint[j][k + 1]] = 1;
					int fangkuai = getIndex(j,k+1);
					visitfangzhen[fangkuai][mapint[j][k + 1]] = 1;
				}
			}
		}

		dfs(1,1,0);

		for (j = 1; j <= 9; j++)
		{
			for (k = 1; k <= 9; k++)
			{
				printf("%d", mapint[j][k]);
			}
			printf("\n");
		}
	}
	return 0;
}