简介
贝塞尔曲线于1962年,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发,以稳定数值的方法求出贝塞尔曲线。
实例
线性贝塞尔曲线
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出:
且其等同于线性插值。
二次方贝塞尔曲线
二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
-
![\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2 \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/8/a/d/8adc5cc34ea9649d6e546043fce9c407.png) 。
。
TrueType字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。
三次方贝塞尔曲线
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
曲线的参数形式为:
-
![\mathbf{B}(t)=\mathbf{P}_0(1-t)^3+3\mathbf{P}_1t(1-t)^2+3\mathbf{P}_2t^2(1-t)+\mathbf{P}_3t^3 \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/5/9/7/597ecc5022fa7ab65509d5edfa9c148c.png) 。
。
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝塞尔样条组成的三次贝塞尔曲线,用来描绘曲线轮廓。
一般化
 阶贝塞尔曲线可如下推断。给定点P0、P1、…、Pn,其贝塞尔曲线即
阶贝塞尔曲线可如下推断。给定点P0、P1、…、Pn,其贝塞尔曲线即
-
![\mathbf{B}(t)=\sum_{i=0}^n {n\choose i}\mathbf{P}_i(1-t)^{n-i}t^i ={n\choose 0}\mathbf{P}_0(1-t)^nt^{0}+{n\choose 1}\mathbf{P}_1(1-t)^{n-1}t^{1}+\cdots+{n\choose n-1}\mathbf{P}_n(1-t)^{1}t^{n-1}+{n\choose n}\mathbf{P}_n(1-t)^{0}t^n \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/d/5/7/d57ace5c0116617a6e9cced0cbdb6abd.png) 。
。
例如 :
:
-
![\mathbf{B}(t)=\mathbf{P}_0(1-t)^5+5\mathbf{P}_1t(1-t)^4+10\mathbf{P}_2t^2(1-t)^3+10\mathbf{P}_3t^3(1-t)^2+5\mathbf{P}_4t^4(1-t)+\mathbf{P}_5t^5 \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/d/b/4/db41ef611ab1eedb0606d9bce9012c30.png) 。
。
如上公式可如下递归表达: 用 表示由点P0、P1、…、Pn所决定的贝塞尔曲线。则
表示由点P0、P1、…、Pn所决定的贝塞尔曲线。则
用平常话来说, 阶的贝塞尔曲线,即双
阶的贝塞尔曲线,即双 阶贝塞尔曲线之间的插值。
阶贝塞尔曲线之间的插值。
术语
一些关于参数曲线的术语,有
即多项式
又称作n阶的伯恩斯坦基底多项式,定义00 = 1。
点Pi称作贝塞尔曲线的控制点。多边形以带有线的贝塞尔点连接而成,起始于P0并以Pn终止,称作贝塞尔多边形(或控制多边形)。贝塞尔多边形的凸包(convex hull)包含有贝塞尔曲线。
注解
- 开始于P0并结束于Pn的曲线,即所谓的端点插值法属性。
- 曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的,贝塞尔曲线是直线的充分必要条件是控制点共线。
- 曲线的起始点(结束点)相切于贝塞尔多边形的第一节(最后一节)。
- 一条曲线可在任意点切割成两条或任意多条子曲线,每一条子曲线仍是贝塞尔曲线。
- 一些看似简单的曲线(如圆)无法以贝塞尔曲线精确的描述,或分段成贝塞尔曲线(虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为
 时,分成四段的贝塞尔曲线,可以小于千分之一的最大半径误差近似于圆)。
时,分成四段的贝塞尔曲线,可以小于千分之一的最大半径误差近似于圆)。 - 位于固定偏移量的曲线(来自给定的贝塞尔曲线),又称作偏移曲线(假平行于原来的曲线,如两条铁轨之间的偏移)无法以贝塞尔曲线精确的形成(某些琐屑实例除外)。无论如何,现存的启发法通常可为实际用途中给出近似值。
建构贝塞尔曲线
线性曲线
![线性贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/8/89/Bezier_1_big.gif/240px-Bezier_1_big.gif) |
| 线性贝塞尔曲线演示动画,t in [0,1] |
线性贝塞尔曲线函数中的t会经过由P0至P1的B(t)所描述的曲线。例如当t=0.25时,B(t)即一条由点P0至P1路径的四分之一处。就像由0至1的连续t,B(t)描述一条由P0至P1的直线。
二次曲线
为建构二次贝塞尔曲线,可以中介点Q0和Q1作为由0至1的t:
- 由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。
- 由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。
- 由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。
 | ![二次贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2d/Bezier_2_big.gif/240px-Bezier_2_big.gif) | |
| 二次贝塞尔曲线的结构 | 二次贝塞尔曲线演示动画,t in [0,1] |
高阶曲线
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1所建构:
 | ![三次贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/ff/Bezier_3_big.gif/240px-Bezier_3_big.gif) | |
| 三次贝塞尔曲线的结构 | 三次贝塞尔曲线演示动画,t in [0,1] |
对于四次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2、Q3,由二次贝塞尔曲线描述的点R0、R1、R2,和由三次贝塞尔曲线描述的点S0、S1所建构:
 | ![四次贝塞尔曲线演示动画,t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7d/Bezier_4_big.gif/240px-Bezier_4_big.gif) | |
| 四次贝塞尔曲线的结构 | 四次贝塞尔曲线演示动画,t in [0,1] |







![\mathbf{B}(t)=\mathbf{P}_0 + (\mathbf{P}_1-\mathbf{P}_0)t=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1]](http://upload.wikimedia.org/math/0/5/c/05c4210c69ffb1358ceb8eb83a1a06fe.png)
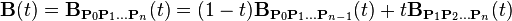
![\mathbf{B}(t) = \sum_{i=0}^n \mathbf{P}_i\mathbf{b}_{i,n}(t),\quad t\in[0,1]](http://upload.wikimedia.org/math/3/d/8/3d8f42d9608ecbd44e2f57758d159eb2.png)
















 1202
1202

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








