堆排序c语言实现

1 什么是堆

堆的定义

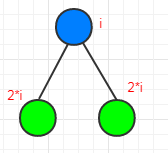
把这个关系 和完全二叉树对应起来，如下图，如果 下标 从1 开始， 这 任意一个节点 i 2*i +1 2*i +2

对于小标从 i ==1 下标从0开始i ==0 的情况

来看下 下面 是 不是堆 ？

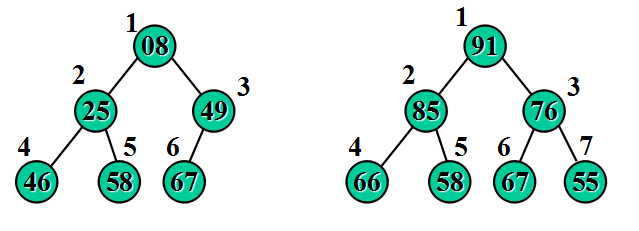
左面 是 小顶堆 ; 右面是 大顶堆

看看下面的图形

左边 3 6 7 不满足 大顶堆的定义， 中间 大顶堆 右面 是 大顶堆

2 堆的存储的结构

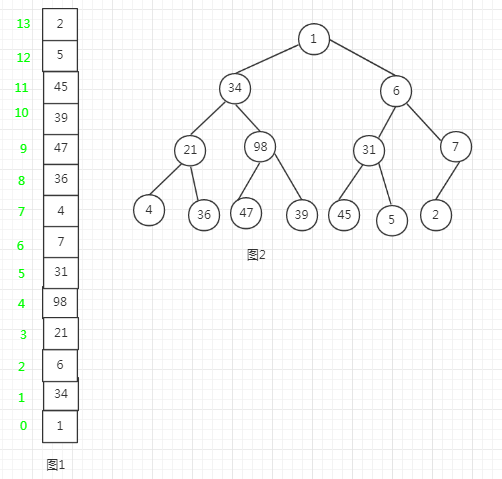
图1 为 实际 存储结构 ， 图2 右面 放在 完全二叉树中的逻辑结构。

3 如何建立 大顶堆

用上面的结构为例 进行图解

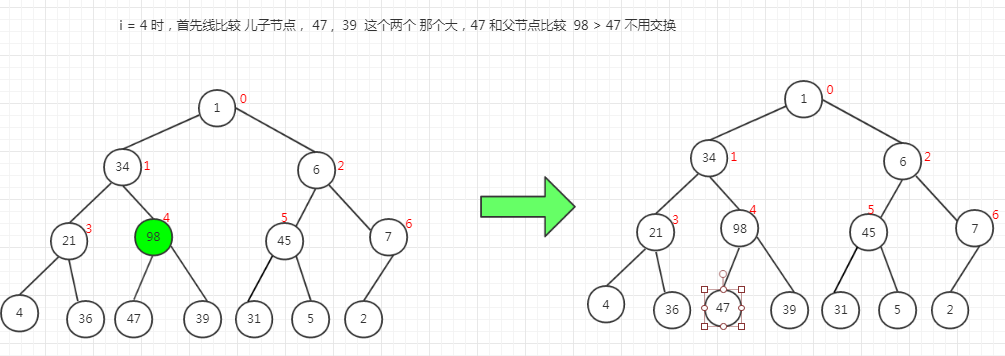
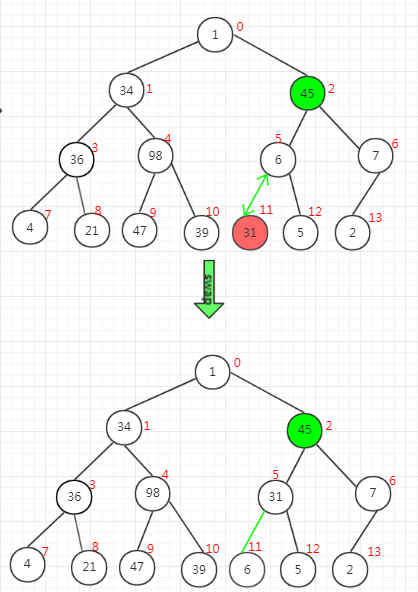
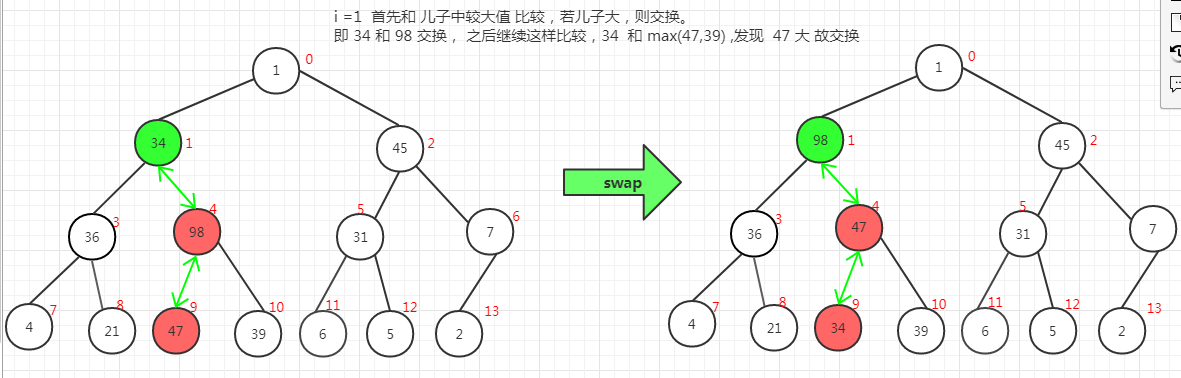
此时建立 了 大顶堆, 将 第0 个元素的 待排序列中的最后一个位置互换位置。 之后对 0 ---> 12 进行 最大堆调整 即可，

直到i==0 时候， 待排 序列 就全部完成， 此时 arr[] 排成的 升序啦。。

4 开始 调整堆

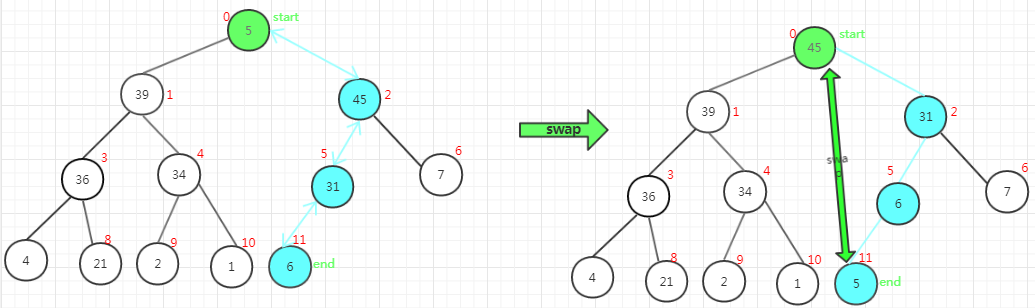
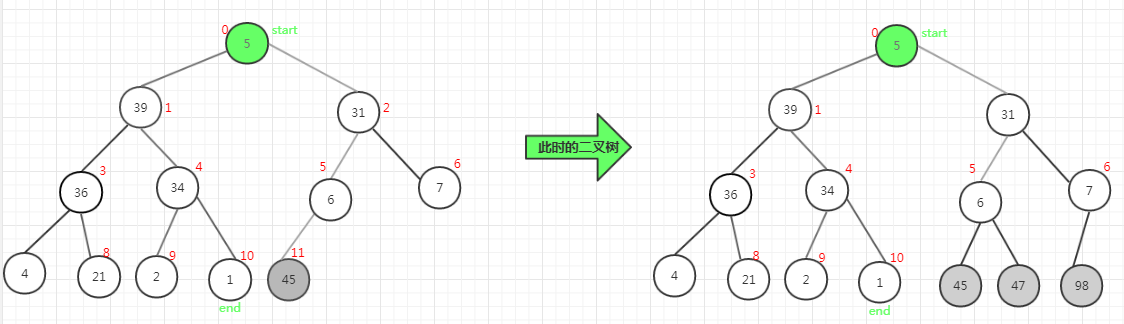
同理 一直这样调整 堆 把调整成 大顶堆， 之后将堆顶的元素和待排序列的最后的一个元素 互换值，之后 带排序序列减1 ， 已排序列 加1 。

最后 i ==0 ,此时就剩一个 待排序列 ，也就完成了所有的排序。

5 堆排序的过程

堆排序的过程是：

(1)建立一个堆array[0..n-1]。

(2)把堆首（最大值）和堆尾互换。

(3)把堆的尺寸缩小1，然后调整堆，目的构成新的堆。

(4)重复步骤2，直到堆的尺寸为1,排序完成。

6 看一下 代码实现：

#include <stdio.h>  

/* 交换元素 */  
void  swap (int array[], int i, int j){
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

void  printAaray(int array[] ,int len){
       for(int i=0; i < len; i++){
         printf("%d  ", array[i]);

        }
       printf("\n");
}


/* 调整堆 */  
void heap_ajust(int arr[], int start, int end) {  
    //建立父节点下标和子节点下标  
    int dad = start;  
    int son = dad * 2 + 1;  
    while (son <= end) { //   
        if (son + 1 <= end && arr[son] < arr[son + 1]) //先比较两個子节点大小，选择最大的  
            son++;  
        if (arr[dad] > arr[son]) //如果父节点大于子节点代表调整完毕，直接跳出函数  
            return;  
        else { //否则交换父子內容再继续子节点和孙节点比较  
            swap(arr,dad,son);  
            dad = son;  
            son = dad * 2 + 1;  
        }  
    }  
}  
  

/* 堆排序 */  
void heap_sort(int arr[], int len) {  
    int i;  
    //初始化堆，i从最后一個父节点开始调整  
    // 建立最大堆 
    for (i = len / 2 - 1; i >= 0; i--) {
        heap_ajust(arr, i, len - 1);  

    }       
    //先将第一個元素和已排好元素前一位做交换，再从新调整，直到排序完毕  
    for (i = len - 1; i > 0; --i) {  
        
        swap(arr,0,i);
        heap_ajust(arr, 0, i-1);  
    }  
}  
  
int main(int argc, char const *argv[]) {  

    int arr[]={1,34,6,21,98,31,7,4,36,47,39,45,5,2};
    int length = sizeof(arr) / sizeof(int);  
    /* sort */  
    heap_sort(arr, length);  
      
    /* print Array */   
    printAaray(arr,length);
  
    return 0;  
}  

7总结

堆排序 效率 ，我这里就不分析了 ，时间效率，nlogn , 是一个不稳定的算法。

参考资料：

http://blog.csdn.net/daiyudong2020/article/details/52529791

堆排序 Heap Sort

http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html

分享快乐，留住感动。 2017/10/23 21:57:13 ---biaoge