点至3D矩形的最近点
实际上等同于计算OBB上的最近点,其中3D矩形可看做是z向为0的OBB。
struct Rect {
Point c;
Vector u[2];
float e[2];
}令z轴为0并重写函数ClosestPtPointOBB()
//Given point p, return point q on (or in) Rect r, closest to p
void ClosestPtPointRect(Point p, Rect r, Point &q)
{
Vector d = p - r.c;
//Start result at center of rect; make steps from there
q = r.c;
//For each rect axis...
for(int i = 0; i < 2; i++) {
//...project d onto that axis to get the distance
//along the axis of d from the rect center
float dist = Dot(d, r.u[i]);
//if distance farther than the rect extents, clamp to the box
if(dist > r.e[i]) dist = r.e[i];
if(disr < -r.e[i]) dist = -r.e[i];
//Step that distance along the axis to get world coordinate
q += dist * r.u[i];
}
}点至三角形的最近点
给定三角形ABC以及一点P,且令ABC上距P的最近点为Q。一种解决方案是:如果P正交投影后位于三角形内部,则投影点即为最近点Q,如果P的正交投影位于三角形ABC的外部,则最近点位于三角形的某一边上。此时则遍历每一条边(AB、BC、CA),计算并返回P的最近点。但明显此种方法并不高效。一种较好的算法是:考查P位于三角形的哪一个Voronoi特征域中。一旦确定,只须将P正交投影至该特征域中即可获取最近点Q。
P位于包含顶点A的Voronoi域由穿越A的两个平面的负半空间的交集构成,其法线分别为B-A和C-A。
确定P位于某一边的Voronoi域,可以采用:计算P在ABC上正交投影的质心坐标。
若点P不属于任一顶点或边的Voronoi域,则Q必位于三角形ABC的内部,实际上为正交投影R。

P点在ABC上正交投影的质心坐标为三角形RAB、RBC和RCA的有符号面积与三角形ABC有符号面积之比。令n为三角形ABC的法线,且对于某t值,有R = P - tn,则R = uA + vB + wC的质心坐标(u,v,w)为:u = rbc/abc, v = rca/abc以及w = rab/abc。通过某些向量计算,可以达到一定程度上的简化目的。如,表达式rab可以按如下方式进行简化:
Vector n = Cross(b - a, c - a);
float rab = Dot(n, Cross(a - r, b - r)); //proportional to signed area of RAB
float rbc = Dot(n, Cross(b - r, c - r)); //proportional to signed area of RBC
float rca = Dot(n, Cross(c - r, a - r)); //proportional to signed area of RCA
float abc = rab + rbc + rca; //proportional to signed of ABC
(上面代码中,n应该为垂直于三角形的向量(法线)。Cross代表叉乘,设α为a,b夹角,则Cross(a,b)的数学意义是absinα*n。而三角形中,若已知两边及它们的夹角α,其面积则是0.5*absinα。即三角形ABC的面积=1/2*abs(AB×AC))
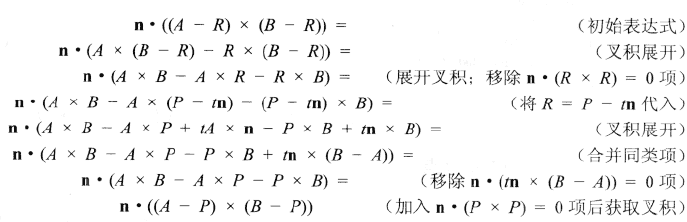
即R的质心坐标可以直接通过P获得,而无须计算R。
于是,首先判断P点是否在三角形3个顶点域内,是则取该顶点为最近点,否则继续判断是否在边域内,若在边域内,取投影在边上的点,否则位于三角形内部,取正交投影坐标R。
(
对下面部分代码的解释:
点投影在直线上:P’ = A + s*AB, s = snom/(snom + sdenom),(snom + sdenom)指AB长度,snom指投影到AB上的长度AP’(snom负表示PA与AB角度大于90度)。
面与面之间夹角:float vc = Dot(n, Cross(a - p, b - p)),vc负表示面之间夹角大于90度。
)
Point ClosestPtPointTriangle(Point p, Point a, Point b, Point c)
{
Vector ab = b - a;
Vector ac = c - a;
Vector bc = c - b;
//Compute parametric position s for projection P’ for P on AB.
//P’ = A + s*AB, s = snom/(snom + sdenom)
float snom = Dot(p - a, ab), sdenom = Dot(p - b, a - b);
//Compute parametric position t for projection P’ of P on AC,
//P’ = A + t*AC, t = tnom/(tnom + tdenom)
float tnom = Dot(p - a, ac), tdenom = Dot(p - c, a - c);
if(snom <= 0.0f && tnom <= 0.0f) return a; //Vertex region early out
//Compute parametric position u for projection P’ of P on BC,
//P’ = B + u*BC, u = unom/(unom + udenom)
float unom = Dot(p - b, bc), udenom = Dot(p - c, b - c);
if(sdenom <= 0.0f && unom <= 0.0f) return b; //Vertex region early out
if(tdenom <= 0.0f && udenom <= 0.0f) return c; //Vertex region early out
//P is outside (or on) AB if the triple scalar product [N PA PB] <= 0
Vector n = Cross(b - a, c - a);
float vc = Dot(n, Cross(a - p, b - p));
//If P outside AB and within feature region of AB,
//return projection of P onto AB
if(vc <= 0.0f && snom >= 0.0f && sdenom >= 0.0f)
return a + snom / (snom + sdenom) * ab;
//P is outside (or on) BC if the triple scalar product [N PB PC] <= 0
float va = Dot(n, Cross(b - p, c - p));
//If P outside BC and within feature region of BC,
//return projection of P onto BC
if(va <= 0.0f && unom >= 0.0f && udenom >= 0.0f)
return b + unom / (unom + udenom) * bc;
//P is outside (or on) CA if the triple scalar product [N PC PA] <= 0
float vb = Dot(n, Cross(c - p, a - p));
//If P outside CA and within feature region of CA,
//return projection of P onto CA
if(vb <= 0.0f && tnom >= 0.0f && tdenom >= 0.0f)
return a + tnom / (tnom + tdenom) * ac;
//P must project inside face region. Compute Q using barycentric coordinates
float u = va / (va + vb + vc);
float v = vb / (va + vb + vc);
float w = 1.0f - u - v; // = vc / (va + vb + vc)
return u * a + v * b + w * c;
}以上代码调用了4次叉积运算。与点积运算相比,叉积运算通常成本较高。因此,采用某种更加经济的表达式是值得考虑的。根据拉格朗日恒等式:
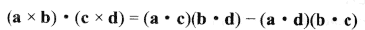
可表示3个标量三重积:
Vector n = Cross(b - a, c - a);
float va = Dot(n, Cross(b - p, c - p));
float vb = Dot(n, Cross(c - p, a - p));
float vc = Dot(n, Cross(a - p, b - p));
并利用6个点积计算对以下内容进行表达:
float d1 = Dot(b - a, p - a);
float d2 = Dot(c - a, p - a);
float d3 = Dot(b - a, p - b);
float d4 = Dot(c - a, p - b);
float d5 = Dot(b - a, p - c);
float d6 = Dot(c - a, p - c);
最终有:
float va = d3 * d6 - d5 * d4;
float vb = d5 * d2 - d1 * d6;
float vc = d1 * d4 - d3 * d2;
实际上,d1~d6也可以用于计算snom、sdenom、tnom、tdenom、unom以及udenom:
float snom = d1;
float sdenom = -d3;
float tnom = d2;
float tdenom = -d6;
float unom = d4 - d3;
float udenom = d5 - d6;
其中向量n不再需要。
点到四面体的最近点
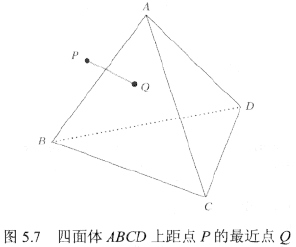
给定点P,当前问题为:计算四面体ABCD上(或之内)距离点P的最近点Q。一种较为直接的算法是:针对四面体中的每一个面,调用函数ClosestPointTriangle()并计算最近点。在多个计算结果中,返回距点P最近的点Q。独立于距离测试,还需要考查点P是否位于四面体中的面内。若P位于四面体中某一面内,则其即为最近点。
//Test if point and d lie on opposite side of plane through abc
int PointOutsideOfPlane(Point p, Point a, Point b, Point c, Point d)
{
float signp = Dot(p - a, Cross(b - a, c - a)); //[AP AB AC]
float signd = Dot(d - a, Cross(b - a, c - a)); //[AD AB AC]
//Points on opposite sides if expression signs are opposite
return signp * signd < 0.0f;
}
上诉算法运行良好且易于实现。然而该算法仍有改进余地。首先,假定顶点P的Voronoi特征域存在,则Q为P在该正交域上的正交投影。针对四面体,需要考查总计14个特征域:4个顶点域、6个边域以及4个面域。若P不属于任何一个特征域,则必定位于四面体内部。
与前述测试方法相比,该算法似乎无明显的性能改观。然而,Voronoi域间却可以共享多数计算过程而无须重复计算。
点到凸多面体的最近点
一种易于实现的、复杂度为O(n)的算法是:计算多面体上每个面中距P的最近点,并返回一个最近结果。同时,还要兼顾测试点P是否位于H各面的背面,即P位于H内部这一情况。为了加速测试过程,面距离测试计算规定:点P位于各面的正面。
对于较大的多面体,一种较为快速的预计算方法为:以层次结构的方式构建多面体的各部分。利用这种预构造的层级方案将使最近点计算的时间复杂度达到log级别。如Dobkin-Kirkpatrick层次结构算法。
此外还有一些高效计算多面体最近点的其他一些算法如GJK算法等。
两直线间的最近点
对于2D空间,两直线不平行则相交,相交时最近点为交点,平行时的最近点为线上任意点。而在3D空间中则未必。故在3D空间中一个较好方案是:若两直线之间彼此并未达到足够接近,则设为不相交(未必平行)。基于此,相交测试转换为两直线间之间的距离,并检测该距离是否小于给定的阀值。
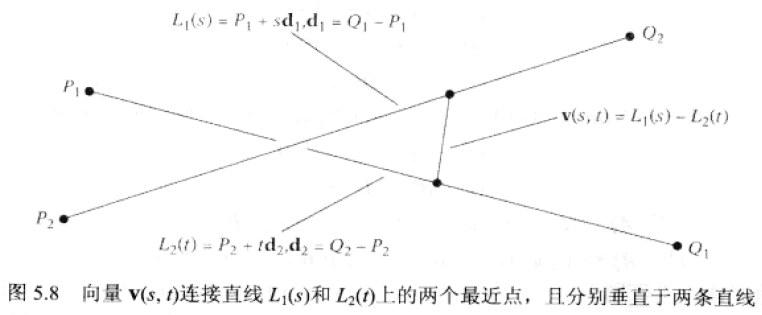
给定L1由顶点Q1,P1连成,L2由顶点Q2,P2连成。
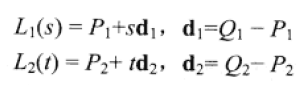
针对s和t的几组计算结果,L1(s)l和L2(t)分别对应直线上的最近点,且v(s, t) = L1(s) - L2(t)。当v具有最小长度值时,两顶点则为最近点。其实即为计算s和t满足以下垂直约束条件:
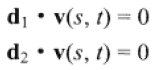
在此省略推导给出结果:
设a = d1·d1, b = d1·d2, c = d1·r, e = d2·d2, f = d2·r, d = ae - b^2
则s = (bf - ce) / d t = (af - bc) / d
注意:当d=0时两直线平行且需要另行处理。
两线段上的最近点
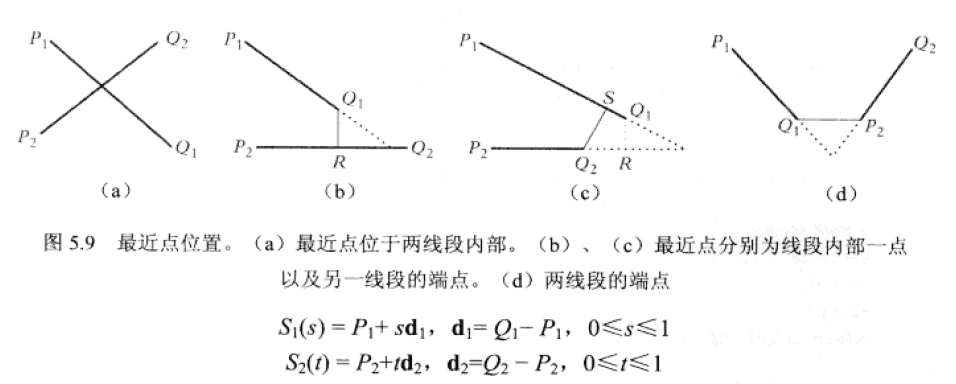
不难看出,在某些情况下,若直线间某一最近点位于相关线段的外部延长线上,该点是可以截取至相应线段的最近端点处。
若直线间的最近点皆位于各自线段的外部延长线上,则上述截取操作需要重复计算两次。
给定直线上L2一点S2(t) = P2 + td2,则L1上最近点L1(s)为:
s = (S2(t) - P1)·d1/d1·d1 = (P2 + td2 - P1)·d1/d1·d1
类似地,给定直线S1上一点S1(s) = P1 + sd1,直线L2上最近点L2(t)为:
t = (S1(s) - P2)·d2/d2·d2 = (P1 + sd1 - P2)·d2/d2·d2
可以使用高斯消元法求解线性方程组。
s = (bt - c)/a
t = (bs + f)/e
其中,a = d1·d1, b = d1·r, e = d2·d2, f = d2·r
2D线段相交计算
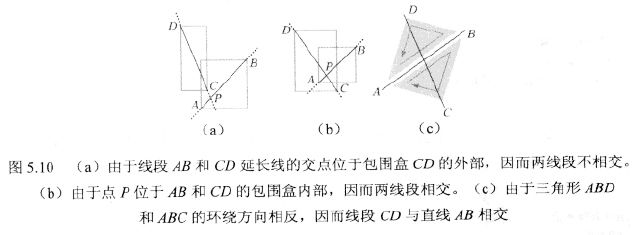
测试两线段AB、CD是否相交,可以首先计算二者(延长线)的交点,且查看该交点是否位于各自线段的包围盒中。需注意的是,需要单独处理两线段平行这一特例。
计算两线段(延长线)交点时,显式定义直线L1的方程L1(t) = A + t(B - A),并隐式定义另一直线方程n·(X - C) = 0,其中n 垂直于CD。利用A+t(B - A)带入方程n·(X - C) = 0并求解t:

则交点P = L1(t)可将t值代入上述显式方程得到。另外,可通过检测0<=t<=1从而确定P是否位于AB包围盒内。
另一种2D线段相交测试方案为:两线段相交仅当两端点彼此位于线段两侧。可以通过判断三角形ABD和ABC的环绕方向加以解决,而三角形的有符号面积可以确定其环绕方向(|a × b| = |a||b|sino ,设点a(x1,y1), b(x2, y2)夹角为o则|a||b|sino = |x1y2 - x2y1|,可得三角形有符号面积为0.5*(x1y2 - x2y1)。 两个非零向量a和b平行,当且仅当|a × b |= 0)。对于某些应用,可以在执行线段相交测试前线处理线段的AABB盒相交测试。对于3D空间内成本高昂的线段相交测试,这一点尤为重要。
//Return 2 times the signed triangle area. The result is positive if
//abc is ccw, negative if abc is cw, zero if abc is degenerate.
float Signed2DTriArea(Point a, Point b, Point c) {
return (a.x - c.x) * (b.y - c.y) - (a.y - c.y) * (b.x - c.x);
}线段和三角形最近点
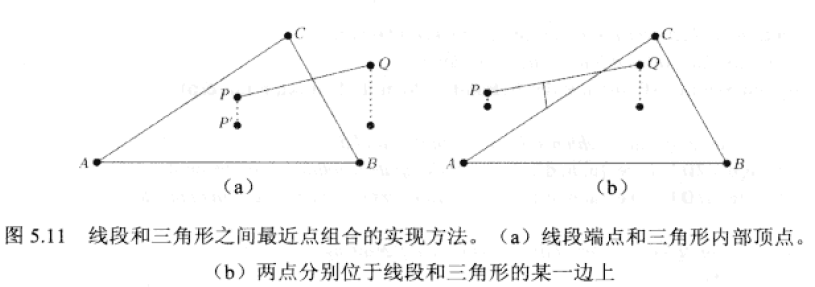
在此不讨论平行情况。
最近点计算涉及下列对象:
线段PQ与三角形边AB
线段PQ与三角形边BC
线段PQ与三角形边CA
线段端点P与三角形平面(P的投影位于三角形ABC内)
线段端点Q与三角形平面(Q的投影位于三角形ABC内)
上述计算返回具有唯一最小距离的最近点作为结果。
在某些情况下,可以适当调整测试的数量以减少计算量。如,若线段两端点投影均位于三角形内部,则无需再执行线段-边的最近点测试,因为最近点必然产生于线段的某一投影点中;若只是线段的一个端点投影位于三角形内部,则只须执行一次相应的线段-边测试;当线段的投影均位于三角形外部,也只须执行一次相应的线段-边测试。对于后两种情况,可以通过计算线段端点所处的Voronoi域确定相关的线段-边测试。
两个三角形之间的最近点计算
两个三角形T1和T2之间的最近点计算一般可认为:相应最近点位于某一个三角形的边上。因此,其结果转化成可对三角形中6条边之间的可能组合,执行线段-三角形的最近点计算。则包含最小(平方)距离的一组点即为最近点集合。
但线段-三角形之间距离测试成本较高。一种较好T1,T2间最近点集测试方案为:一组最近点产生于两个三角形的相应边上,或产生于某一顶点与另一个三角形的内部点之间。问题转化成:计算两三角形间一对边的最近距离,以及顶点与三角形之间的最近点(相应顶点的投影位于三角形内部)。综上,需要执行6次顶点-三角形测试以及9次边-边测试。最终从多组最近点中,选择具有最小距离的一组顶点作为最终三角形间的最近点。
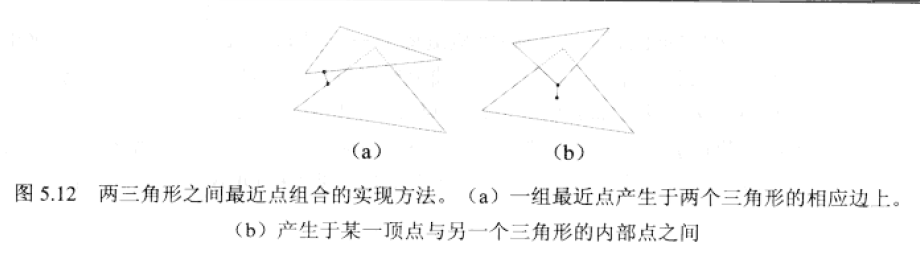
(三角形平行以及重合的情况需要剔除)






















 2537
2537











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








