以下给出一些经典问题以及建模方法。
1.多源多汇问题。源点以及汇点都有多个。
建模:建立超级源点S以及超级汇点T,S向所有源点建边,容量无穷大,所有汇点向T建边,容量无穷大。
2.结点有容量限制。每个结点都有最大允许通过的流量。
建模:将一个结点u拆成两个u、u',所有指向u的有向弧与u建边,所有u出发的有向弧改成从u'出发,u、u'中间建有向弧,流量即点权。
3.无向图最大流。
建模:将反悔边的容量设为和正向边的相同即可。
4.二分图匹配中的最大匹配问题。
建模:源点向X集合中的元素连有向弧,Y集合中的元素向汇点连有向弧,X集合中的u和Y集合的v存在关系则连一条从u到v的有向弧,这些有向弧的容量均为1,最后跑一遍最大流即最大匹配的答案。
5.二分匹配中的最小覆盖集、最大独立集。
建模:按照二分匹配的性质可转化成3。
6.固定起点和终点,求边不相交最短路径数。ZOJ2760 How Many Shortest Path
建模:先跑一次最短路算法,然后将所有在最短路上的边保留,然后按照边的方向建有向弧,弧的容量均为1。最后跑一遍最大流,流量即答案。
7.固定起点和终点,求点不相交最短路径数(起点终点除外)。
建模:先跑一次最短路算法,用建模2的方法拆点,两点间建有向弧容量为1,最短路上的边容量设为无穷大。最后跑一遍最大流,流量即答案。
8.固定起点和终点,求点、边均不相交的最短路(起点终点除外)。
建模:模型6、7的结合。拆点,两点间边权为1,最短路的边容量也为1.最后跑一遍最大流,流量即答案。
结论:模型6、7、8的一般形式:固定起点和终点,求点有使用次数限制,边有使用次数限制的最短路条数。拆点,两点间边权为点次数限制,最短路上的边的容量即边次数限制。
9.区间模型+输出方案。UVa 11167 Monkeys in the Emei Mountain
题目大意:雪雪是一只猴子。它在每天的 2:00 —— 9:00之间非常渴,所以在这个期间它必须喝掉2个单位的水。它可以多次喝水,只要它喝水的总量是2.它从不多喝,在一小时内他只能喝一个单位的水。所以它喝水的时间段可能是2:00 ——4:00,或者3:00——5:00,或者7:00——9:00.甚至喝两次,第一次2:00——3:00,第二次8:00——9:00.但是它不能在1:00——3:00喝水,因为在1:00时它不渴,也不能在8:00——10:00喝水,因为9:00必须结束。
一共有n(n <= 100)只这样的猴子。我们用一个(v,a,b)(0 <= v,a,b <= 50000,a < b,v <= b - a)来描述一个在时间a~b之间口渴,并且必须在这个期间喝够v个单位水的猴子。所有猴子喝水的速度都是1小时喝1个单位的水。
现在的问题是只有一个地方可以让m只猴子同时喝水,需要作出一个能满足所有猴子的喝水需要的安排,问能否给出安排。多解时输出任意一组解即可。
建模:很显然我们可以想到一种方法,建立超级源汇,对每只猴子 i 建边(s,i,v[ i ])其中 s 是源点,v[ i ]是猴子 i 需要喝水的总量。对每个时间点 x 建边(x,t,m)其中 t 是汇点,m表示这个时间点最多同时容纳m只猴子一起喝水。然后再对每个猴子 i 能喝水的时间 x 建边(i,x,1)表示猴子 i 可以在时间 x 喝一单位的水。很显然这样子跑一遍最大流后,如果满流则有解,否则无解。
但是!
由于时间轴有至多50000长,如果按照上述的建边必定超时。
而且我们可以注意到 n 至多100,那么可以划分出来的区间至多199个,我们可以通过离散化缩小数据规模!
首先将每个猴子喝水的时间区间的左右端点存入b[ ]数组中,排序并去除重复元素。接下来,对于每个区间b[ x ] - b[ x- 1 ](暂定区间编号为 x)如果包含于猴子 i 的喝水区间之内,则建边(i,x,b[ x ] - b[ x - 1 ])表示猴子 i 可以在区间 x 中喝至多(b[ x ] - b[ x - 1 ])的水,然后对每个猴子 i 建边(s,i,v[ i ])含义与先前一样,对于每个区间x,建边(x,t,m * (b[ x ] - b[ x - 1 ]))表示区间 x 至多能分配m * (b[ x ] - b[ x - 1 ])的水。
然后跑一次最大流,如果满流则有解,否则无解。
接下来比较让人蛋疼的就是它的输出方案,那么对于每只猴子我们怎么知道它在哪几个区间喝了水?对着从这只猴子出发的反向边检查一下就好啦~,如果有流量说明属于这条边的正向边被流过(也就是说猴子去该边所指向的区间喝水了),且喝的水的容量就是反向边的流量。还有个要考虑的就是如果一个区间被好多猴子一起享用,那么直接对这个区间不断的循环取就好了。
10.混合图的欧拉回路。给你一个同时存在有向边以及无向边的混合图,你需要将所有的无向边定向,使得最后的有向图存在欧拉回路。欧拉回路的定义:所有点的入度=出度。
建模:首先随便给无向边定向。然后给所有点计算入度以及出度。如果此时有一个点的入度与出度的差是奇数,则一定不存在解。
接下来,怎样修改无向边的方向才能满足入度等于出度,假设入度大于出度且入度减出度等于X(X为偶数),现在如果我们改变了这个点上X/2条边的方向则便能使这个点满足入度等于出度。如果每个点的入度都等于出度,则显然存在欧拉回路。
现在我们应该怎么改变边,来使得图存在欧拉回路?原图中的有向边是不能改变方向的,所以无用,删。然后以无向边定向后的图建图,所有边的边权均为1。然后建立超级源S,超级汇T,设Xi等于点i的入度减出度(包括有向边以及定向后的无向边)。我们对入度小于出度的点i建边(S,i,-Xi/2),对于入度大于出度的点i建边(i,T,Xi/2)。最后跑一边从S到T的最大流,如果S出发的弧均满流或者到达T的弧均满流则存在解,否则无解。
我们发现,如果有的边被流过,则说明这条边被反向了。如果要求输出哪些边被反向了,则看反悔边的容量是否为1(正向弧的容量为0),是则被反向。如果进一步要求输出路径,给一个图G,使得图G包含一开始的有向边以及跑完最大流后容量为1的边(包括反向弧),最后在这个图上跑几遍就能得到路径。
11.给定一个矩阵,矩阵内每个方格有一个权值,现在需要你取出一些边不相邻的方格内的权值,使得权值和最大。
建模:经典的最小割模型。最小割是最大流的对偶问题,最小割的容量等于最大流的容量。
建立超级源汇S,T。将图进行黑白染色,S和黑色的方格建边,容量为黑色方格权值,白色方格和T建边,容量为白色方格权值,黑色方格向相邻的白色方格建边,容量为无穷大。最后跑一遍最大流,所有点的权值和减去最大流的流量即答案。
为什么这样是可行的?
因为所有相邻的点之间我们都建立了容量为无穷大的边,也就是说,要么与源点相连的边被割掉,要么与汇点相连的边被割掉,最后跑完最大流后选择出的边的集合便是最小割边集,满足除这些割边之外点之间互相没有边(可以理解为割边集即该二分图的最小点权覆盖集,除割边外的点即二分图的最大点权独立集)。虽然是最大流,但是割的容量却是最小的。局部最大流,全局最小割,这就是最大流和最小割的关系。
12.给定一个矩阵,矩阵内每个方格有一个权值,现在你可以取出一些方格的权值,如果取走了两个相邻的方格内的权值,则需要付出一些代价,你需要使得权值和 - 代价的值最大。
建模:较上面的模型相对有些变化,但还是可以解决的。
建立超级源汇S,T。将图进行黑白染色,S和黑色的方格建边,容量为黑色方格权值,白色方格和T建边,容量为白色方格权值,黑色方格向相邻的白色方格建边,容量为取该两点的代价。最后跑一遍最大流,所有点的权值和减去最大流的流量即答案。
13.给定一个矩阵,矩阵内的方格内有两种属性(假设第一种属性为黑色,第二种为白色),的权值,每个方格可以取走其中一个属性的权值,可以取相邻的数,如果取走的相邻方格属于同一属性,需要花费相应的代价,问怎样取使得权值和-代价的值最大。
建模:现在我们依旧将图黑白染色,方格内属性和染色相同颜色的和源点建边,边权为该属性的权值;方格内属性和染色不同颜色的和汇点建边,边权为该属性的权值。同一方格内的两种属性之间建边,容量为无穷大,表示只能取其中一种属性,相邻方格颜色相同的建边,容量为相应的代价(这里所有边的方向均从源点指向汇点)。最后跑一遍最大流,所有点权值和减去最大流的流量即答案。
结论:像这样类似方格取数的问题,可以进行二分图黑白染色确定点所属的集合,不同集合内的边的边权即约束条件。像模型11,约束条件便是不能取相邻方格,我们让取相邻方格的代价无穷大化使得只能取不相邻集合的点。模型12,约束条件有所改变,边的容量为代价,这样虽然可以取相邻方格的点,但是是需要付出代价的。模型13,只是多了一些约束条件而已。总的来说,不同集合内的点之间的边的边权即这两点之间的约束条件,也即选取代价,对约束条件的理解深刻有利于解决这一类问题。更是可以进行进一步的拓展。
14.最大权闭合子图。给定带全图G(权值可正可负),求一个权和最大的点集,使得起点在该点集中的任意弧,终点也在该点集中。
建模:新增附加源汇S、T,S向所有的正权点建边,容量为权值,负权点向T建边,容量为权值的相反数。图中其他边方向不变边权为无穷大(无向图参照模型3)。求出最小割后,所有点减去被割的边所代表的点即所求的权和最大的点集。所有正权点的点权和减去最小割容量即点集的权和。
原图中边容量无穷大的意义:选择了弧头的点,则一定要选择弧尾的点。因为如果选择了u,则说明S到u的边未满流,这时如果存在边(u,v)且v未被选择,则必定会有一条增广路经过(u,v)。边的容量设为无穷大也是本题的约束条件。
PS:上次做到一道最大权闭合子图,由于存在环,还需要先强连通缩点,然后再做最大流。
15.最大密度子图。给出一个无向图,找到一个点集,使得起点在该点集中的任意弧,终点也在该点集中,且使得这些点之间的边数除以点数的值(称为子图的密度)最大。
建模:因为选择了一条边的两个端点,则必然要选择这条边,那么我们可以将原图中的每个点和边都看成新图中的结点,将问题转化成最大权闭合子图问题。然后就可以采用0-1分数规划求解了。
设E=『e1,e2,...,en』为边集向量,V=『v1,v2,...,vm』为点集向量,其中ei和vi取值均为{0,1},0表示不选,1表示选,且选择符合闭合子图的定义。那么我们就是要求一个最大的选取方案使得r=E/V最大。
我们可以二分r来寻找最大值。首先设立超级源汇S、T,S向所有ei建边,容量为1,所有点vi向汇点建边,容量为二分系数r,所有边ei向该边的两个端点eu,ev建边,容量为无穷大。然后我们跑一遍最大流,如果流量小于边数,说明可以将r上调来使得r=E/V,否则如果流量等于边数,则说明应该调整上界(因为不可能存在m-流量小于0的情况,由于最大权闭合子图的特殊性,小于0的情况被等于0的情况代替)。
最后用求出的r再一次求一次可行解,因为二分最后一步的求解可能得到的是不可行解,而最后得到的r一定是可行解。然后沿着有流量的边跑一次,能到达的点即答案。
16.竞赛图。SGU326Perspective
题目大意:NBA某小组内有N支球队,小组内以及小组间已经进行了若干场比赛。现在给出这N支球队目前胜利的场数、还剩多少场没有比(包括小组内和小组间)以及小组内任意两支球队之间还剩多少场没有比,问能否合理安排剩下的所有比赛,使得球队1最后胜利的场数至少和小组内任何一支其他球队一样。(2 <= N <= 20, 0 <= x <= 10000, x表示其他任何输入)
建模:建立超级源汇S、T。首先让和球队1进行的比赛都让球队1获胜。然后,S和除球队1外所有球队建边,容量为这些球队最多还能能获胜的次数(已经获胜次数+最多能获胜次数不能大于球队1最多能获胜的次数)。所有的不包括球队1的比赛向T建边,容量为1。接下来,一场包括了球队u和v的比赛i建边(u,i,1),(v,i,1),表示这场比赛能让u或者v中的一个赢。最后跑一遍最大流,如果满流,则说明所有的比赛都已经在满足条件下(不超过球队1的分数)分配掉了。这里我们用到了最大流中的一个思想,用最大流的流向确定不确定因素。
17.动态加边的网络流。SGU 438 The Glorious Karlutka River =)
题目大意:有一条东西向流淌的河,宽为 W,河中有 N 块石头,每块石头的坐标(Xi, Yi)和最大承受人数 Ci 已知。现在有 M 个游客在河的南岸,他们想穿越这条河流,但是每个人每次最远只能跳 D 米,每跳一次耗时 1 秒。问他们能否全部穿越这条河流,如果能,最少需要多长时间。 <= N <= 50, 0 < M <= 50, 0 <= D <= 1000, 0 < W(0<= 1000, 0 < Xi < 1000, 0 < Yi < W, 0 <= Ci <= 1000)。
建模:首先将南岸作为源点,北岸作为汇点,如果南岸和北岸的距离小于等于D,则1秒即可。否则,从小到大枚举时刻t(2<=t<=N+M,最少2秒,最多一个一个的过),将石头按照时间拆开,每一个时刻,源点向该时刻能从南岸直接跳到的石头建边,该时刻的石头向能直接跳到的汇点建边,容量均为石头能承受的人数,然后所有能从石头u跳到石头v的,从t-1时刻的石头u向t时刻的石头建边,容量为石头u的容量,每一层建完以后跑一遍最大流,如果流量等于人数时即可停止,这时的t即答案。这题涉及到动态添加边,我们可以在建边的时候保存下来这条边一开始的容量,在最大流之后,再用这个容量去初始化最大流后网络中边的容量即可。
18.二分加网络流。
这个倒是经常网络流会考到的方法。感觉没啥能说的,遇到了自然就会的。
19.项目分配问题。
先来看一个函数。

项目分配问题便和这个函数息息相关的,因为用网络流可以求解这个函数的最小值。
建模:建立超级源汇S、T。S向所有的Xi建边,容量为ai,表示如果Xi取1则有ai的代价;所有的Xi向T建边,容量为bi,表示如果Xi取0则有bi的代价;然后存在(i,j)关系的Xi向Xj建边,容量为Cij,表示如果Xi取1,Xj取0时有Cij的代价。
最后跑一遍最小割,割的容量即该函数的最小值,也即取值的代价最小。
因为这样建模后,Xi要么取1,要么取0,又由于最小割的局部最大流全局最小割的特性,求出的最大流即最小割,割掉的边即Xi的取值,如果割掉了S和Xi之间的边,则说明Xi取1,否则Xi取0。这里我们又用到了网络流的特性:用流量的流向确定一些变量的取值。
让我们来看几道例题。
该题就是这个函数的基本原型。直接套用即可。
例二、【ZOJ】2539 Energy Minimization
本题稍作改变,只是将代价变成了绝对值而已,仍旧可以轻松解决。
本题略显复杂,一开始我们能得到一个显而易见的函数:

然后我们将这个式子进行一步步的分解,使其接近我们能求解的函数:

得到函数一个这样的形式以后,很惊讶的可以发现,等式右端括号里的部分和之前的f函数的定义惊人的相似!
当ai取1的时候,需要割掉代价为sum{bij}(1 <= j <= N)的S->Xi边,当ai取0的时候需要割掉代价为ci的Xi->T边,当ai取1且aj取0时需要割掉代价为bij的i->j边。
这个我们跑一遍最小割即括号中函数的最小值,用bij的总价值减去最小割的值即最大的D。
20.行列模型。【HDU】4975 A simple Gaussian elimination problem.
题目大意:告诉你每一行的元素和,每一列的元素和,每个元素的取值范围。如果无解输出“So naive!”。如果多解输出“So young!”。如果有唯一解,输出“So simple!”。
建模:首先每行i用一个结点ri表示,每列j用一个结点cj表示,建立超级源汇,源点向ri建边,容量为行i的元素和。cj向汇点建边,容量为列j的元素和。所有行向所有列建边,容量为取值上限。如果流量等于所有元素的和并且所有行的元素和等于所有列的元素和,则存在解,否则无解。然后需要判断是否多解。因为一个子四边形的四个角上的元素满足一个对角线上的元素都可以减小并且另一对角线上的元素都可以增大则存在多解。
判断是否多解这里有两种方法。
方法一:先扫描一下所有的边,(i,j)的反悔边容量即矩阵内[i][j]的容量假设扫描到了第r行,以vis[i][j]标记r行之前的位置i元素是否可以减小以及位置j元素是否可以增大,如果存在则vis[i][j]=1,否则vis[i][j]=0,现在看第r行的位置i以及位置j,如果位置i元素可以增大,则说明存在多解。否则等判断完r行的[i][j]以及[j][i]后更新vis[i][j]以及vis[j][i]。如果到最后都没有符合条件的子四边形存在则说明有唯一解。这里我们可以加一个优化,判断的时候如果该行(列)元素全部为0或者全部为最大值则可以跳过,因为即使存在也不会在这一行(列)内选择,该行(列)内是找不到需要的解的。
方法二:可以想到,如果选择一条边递归,然后从递归里出来了,说明没找到环,那么走这条边肯定找不到环,以后也不用走了,可以把这条边删了。或者这条边流量为0,也可以删了。
这样的话每条边最多只进一次,O(m)。参见http://www.cnblogs.com/yuiffy/p/3929369.html
建模:每条边按照容量大小x拆成x条,容量依次为a,3a,5a,7a......因为最小费用最大流每次一定是先走最小费用的边,所以走的一定是先选小的边,而前k小的边的权和正好是ak^2,和原题的要求等价。
22.网络中边权有正有负的最小费用流。
建模:如果没有负费用圈,则只需在增广到增广路费用为正时停止即可。如果存在负费用圈,则应该先用消圈法消去负圈。
23.区间K覆盖问题。数轴上有一些带权值的左闭右开的区间,选出权和尽量大的一些区间,使得任意一个数最多被K个区间覆盖。
建模:将数轴上的每个数看作一个结点,对于每个权值为w的区间[u,v),建边u->v,容量为1,费用为-w,然后每个数轴上的点i向第i+1个点建边i->i+1,容量为K,费用为0。源点向最左点建边,容量为K,最右点向汇点建边,容量为K,最后求源点到汇点的最小费用最大流即可。如果数轴太大可以进行离散化。如果区间是其他类型的区间,则稍微做一些转化即可。
24.最小割的关键割边。【ZOJ】2532 Internship
首先要明确关键割边的含义:增加这条边的容量则网络的流量即会增加。
建模:首先按照题目要求跑一遍最小割(最大流)。然后在残余网络上进行dfs(即只走有流量的边),先从源点开始进行dfs,将能到达的所有点都标记为1,然后从汇点开始再进行一次dfs,将能到达的点都标记为2。最后判断所有原图中的边(只看正向边),如果该条边的弧头被标记为1,弧尾被标记为2,则说明这条边即关键割边。
25.K路径覆盖问题。【HDU】4862 Jump
给定一个N*M的矩阵,矩阵每个格子中有一个值(0~9),一开始你有活力值为0,然后你可以进行最多K次游戏,每次可以任选矩阵中的一个点作为顶点,然后开始游戏,每次你可以选择从这个点跳到它的右边的点或者下边的点或者不动。每次跳跃,你将支付两个点的曼哈顿距离-1的活力值,能量值可以为负。如果一次跳跃的起点和终点的格子中的值相同,你的活力值可以增加这个值大小的值。每个格子最多只可以经过一次且必须经过一次。每次游戏你可以跳任意多次,但不能违反规则。问最后能得到多少的活力值,如果不能遍历完所有点则输出-1。
建模:建立超级源汇S、T,S向所有格子建边,容量为1,费用为0,所有格子拆成两个,分别为i,i',i到i'之间建边,容量为1,费用为比所有点的权和还小即可(可设为-1e5),保证优先遍历所有点。然后所有点向其右边的点j建边(i',j,1,k-1-a),其中k-1为跳跃长度为k的花费,当一次跳跃的起点以及终点权值相同时,a等于该权值,否则,a等于0。所有点向其下方的点建边同上。最后建立超超级源汇S',T',S'向S建边,容量为K,费用为零,T向T'建边,容量为K,费用为0。最后跑最小费用流,如果cost的相反数/100000等于遍历的N*M(即遍历的所有点),则答案即(-cost)%100000,否则输出-1。
这里需要注意的是,由于最大流的是否并不一定是最小费用,所以在增广到增广路权和为正时即可退出费用流算法。
26.最大费用循环流。UVa 1659 Help Little Laura
题目大意:平面上有m条有向线段连接了n个点。你从某个点出发顺着有向线段行走,给走过的每条线段涂一种不同的颜色,最后回到起点。你可以多次行走,给多个回路涂色(要么不涂色,要么就至少给一个回路上的边全部涂色)。可以重复经过一个点,但不能重复经过一条有向线段。如下图所示的是一种涂色方法(虚线表示未涂色)。
每涂一个单位长度将得到X分,但每使用一种颜色将扣掉Y分。假设你拥有无限多种的颜色,问如何涂色才能使得分最大?输入保证若存在有向线段u -> v,则不会出现有向线段v -> u。n <= 100,m <= 500,1 <= X,Y <= 1000。
对于坐标(x,y)0 <= x,y <= 1000。
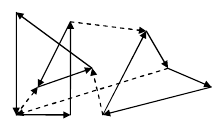
建模:对于一条边(i,j)如果Y-X*dist(i,j)为非负数建边(i,j,1,Y-X*dist(i,j)),如果Y-X*dist(i,j)为负数,建边(j,i,1,X*dist(i,j)-Y),记录下负费用,同时S向j建边,容量为1,费用为0,i向汇点建边,容量为1,费用为0,最后跑一遍源点到汇点的最小费用最大流,答案即费用减去负费用之和(负费用之和指的是绝对值)的相反数。一个环中被源点建边的次数以及被汇点建边的次数一定是相等的,且边方向的选择具有连锁反应,最后跑出来的流要么都是顺时针,要么都是逆时针的。将负费用之和先记录下来的原因是,如果跑的是一个和正权边同方向的环,则说明环中正权边的费用-负权边的费用是正数,带来收益,答案应该加上环中正权边减去负权边的权值和,如果跑的是一个和负权边同方向的环,则说明说明环中正权边的费用-负权边的费用是非正数,并没有带来收益,则此时费用等于负权值的费用,费用减去负权值的费用等于0,说明不对这个环进行涂色。最大权闭合子图的答案和这个是类似的思想。
27.二分图中的很多带权问题都可以转化成费用流求解。
28.双重边权问题。 HDU4067 Random Maze
此类问题,一条边存在两个边权,需要在题目限制内选择其中一个边权以达到所需的最优值。
题目大意:
一个可行图需要满足以下条件:
1.所有的路都是单向的;
2.对于入口 : 出度 = 入度 + 1;
3.对于出口 : 入度 = 出口 + 1;
4.对于其他点 : 入度 = 出度;
给你一个有向图,n个点,m条边,起点S,终点T,每条边存在图中要花费a元,从图中删除要花费b元。问最少需要花费多少使得图成为一个可行图。
建模:
易知,如果是一个可行图,则添加T到S的边恰好是一个欧拉回路(所有点的出度 = 入度)。
怎样建图好呢?我们可以先贪心建图,将花费最小的情况构建出来,不管是否可行!
*对于每条边(u,v),如果a > b,则建边(v,u,1,a - b),sum += b,默认这条边是不存在于图中的,由于不存在图中所以点的出度及入度不变化。
*对于每条边(u,v),如果a <= b,则建边(u,v,1,b - a),sum += a,默认这条边是存在于图中的,且++deg[u], --deg[v],这里deg[u] = out[u] - in[u]。
*对于S,T,连接(T,S),即++deg[T], --deg[S](就是为了使得图中每个点的状况能够相同,并非真正的连接S-T)。
至此,最小情况构建完毕,接下来我们该怎么才能使得整幅图符合条件?
首先,添加超级源s,超级汇t。
由构图方法可以知道,对于每个点u,如果deg[u] > 0,说明从它出发的边大于指向它的边,建边(s,u,deg[u],0),输出流量,选择恢复指向它的边或者删除从它出发的边,流量用完则该点的出度 = 入度。对于每个点v,如果deg[v] < 0,说明从它出发的边少于指向它的边,建边(v,t,deg[v],0),接收流量,选择恢复从它出发的边或者删除指向它的边,全部接收则该点的出度 = 入度。
对于图中的每个点,流向它的边有两种情况,从它出发的边也有两种情况。当流向它的是原图的正向边时(即在原图中b >= a),流过它的时候,相当于删除这条边。接下来从这个点出发,当流出的边是原图的正向边时(即在原图中b >= a),相当于删除这条边,恰好与流进的边抵消,度保持不变;当流出的边是原图的反向边(即在原图中b < a),相当于恢复了指向它的反向边,同样抵消了入边的影响。对于指向该点的是原图的反向边时(即在原图中b < a)同理。对于出度大于入度的点,接收源点流出的流量相当于给它机会抵消多余的出度;对于入度大于出度的点,流量流入汇点相当于给它机会抵消多余的入度;对于中间点,由上述可知无论怎么流都不会影响他们的出入度平衡。
最后,只要跑一次最小费用最大流,如果满流(即流量等于多余的入度或者多余的出度),则有解,解为一开始存在于图中的费用sum+流量flow;否则无解。另外可知,如果有解,则所有流过的边都是需要恢复或者删除的边。
29.K取方格数问题。POJ 3422Kaka's Matrix Travels
题目大意:给定一个N*M的矩阵。每次游戏可以选择一条以矩阵左上角为起点,右下角为终点的路径,取走在这条路径上的所有方格内的权值。现在你有K次机会进行游戏,问最多能得到多少的权值。其中每个点可以被重复经过,但每个点上的权值最多只能被取走一次。
建模:每个点拆成两个点i、i',建边i->i',容量为1,费用为-w,同时再建边i->i',容量为无穷大,费用为0,表示每个点上的权值最多只能被取走一次且每个点能被经过多次。每个点u向它右边的点v建边u'->v,容量为无穷大,费用为0。向下同理。最后建立超级源汇S、T,S向矩阵左上角的点建边,容量为K,费用为0,矩阵右下角的点向汇点建边,容量为K,费用为0。最后跑一遍S到T的最小费用最大流,费用的相反数即答案。
30.按点的属性建分属性图。LA 5905 Pool construction
题目大意:给定一个N * M的网格型地图,其中有的地方是坑,有的地方是草地,将草地变成坑需要花费D,将坑变为草地需要花费F,将坑的边界包围起来需要每单位花费B(因为以后要将坑灌水变成水池,为了防止水溢出,需要围起来)。其中坑可以不连续的分布,但是地图的最外围必须是草地(也就是说只能把坑补上)。问要将所有的坑的边界围起来需要花费的最小值是多少。
建模:每个点有两个属性,坑、或者是草。
最外围的坑必须是草,这个我们预处理解决掉。
然后我们建立超级源汇S、T。
S向草建边,容量为D,表示如果割掉S和草的联系,将这棵草变成坑所需要的代价。
坑向T建边,容量为F,表示如果割掉坑和T的联系,将这个坑变成草所需要的代价。
然后所有相邻的两个点之间建无向边,容量为B,如果有流量从源点流向汇点,则必定是经过了(草->坑)边。
最后我们对最外围的草建边S-草,容量为无穷大,表示这个草一定不会变成坑(绝对不会割掉S-草边)
现在我们要做的就是将一些草变成坑(割掉S-草边),将一些坑变成草(割掉坑-T边)来使得最后从源点到汇点的流量最小。该最小流量的定义便是最小割。
依旧是那句话:局部最大流,全局最小割,虽然对于局部来说是最大流,但是对于全局来说这是最小流。
还是那个道理:用网络流来(割)决定所有点的属性。
31.预流&填坑。【BZOJ】1061 [Noi2008]志愿者招募
题目大意:申奥成功后,布布经过不懈努力,终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难题:为即将启动的奥运新项目招募一批短期志愿者。经过估算,这个项目需要N 天才能完成,其中第i 天至少需要Ai 个人。 布布通过了解得知,一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天,招募费用是每人Ci 元。新官上任三把火,为了出色地完成自己的工作,布布希望用尽量少的费用招募足够的志愿者,但这并不是他的特长!于是布布找到了你,希望你帮他设计一种最优的招募方案。
建模:设每个时间i都需要有至少Ai个志愿者,设每种志愿者i使用了xi个,那么我们对于每个时间点都可以列出一个不等式:x1+x2+x3+...+xn>=Ai(其中如果第i类志愿者不能在该区间工作则xi固定为0)。
最后要求最小化w1*x1+w2*x2+x3*x3+...+wn*xn(其中wi是第i种志愿者的单位价格)。
这正是一个线性规划的问题。
那么我们是否可以转化为网络流来求解呢?
当然可以!
现在我们将每个点的Ai取反,变成-Ai,这样他就成了一个“坑”了(相对于y=0而言),我们从源点S给最左边的时间点引流,流的大小为U(U为大整数),然后每个时间点i向时间点i+1建边(i,i+1,U-Ai,0),最后设汇点为最右端的时间点。
现在,如果所有时间点的Ai都为0,那么显然,汇点的流量恰好等于U。
问题来了,现在我们有的Ai不等于0了,那么显然源点到汇点的流量被这些“坑”所截断了,怎么解决这一个问题?
假设志愿者工作的时间为【Li,Ri】,且该种志愿者单位花费为Ci,则我们建边(Li,Ri+1,INF,Ci),表示我们雇佣了一些志愿者“填坑”来了,如果雇佣了xi个志愿者,则说明将该区间内的所有“坑”的深度填掉了xi(当然可能有的坑在“填坑”行动后高于y=0,那也无所谓了嘛,多多益善~)。
那么现在是不是看起来思路有一点清晰了?
于是志愿者的作用就是一个人可以填一个区间的“坑”(好厉害!),然后需要每种志愿者选择一些使得花费最小的情况下填掉所有的“坑”,就是这样~
最后就是让费用流帮我们选择志愿者的时候了~
于是我们按照上面的方法跑完一遍最小费用最大流,如果流量等于U,则说明满流(志愿者们成功填掉了所有的坑,同志们辛苦了~),此时的记录的cost就是最小值(cost为算法记录的最小费用)。如果流量不等于U则无解。
这时我们又收获了一种费用流的模型:初始给一道大流,然后将有至少覆盖次数限制的点(边)的权值取反变成“坑”,最后区间覆盖就等于“填坑”,只要最后的流量等于大流的流量,就有解。
32.上下界网络流。
1.无源汇上下界可行流
建图模型:
du[i]=in[i](i节点所有入流下界之和)-out[i](i节点所有出流下界之和)。
当du[i]大于0的时候,st到i连一条流量为du[i]的边。
当du[i]小于0的时候,i到sd连一条流量为-du[i]的边。
最后对(st,sd)求一次最大流即可,当所有附加边全部满流时(即maxflow==所有du[]>0之和),有可行解。
2.有源汇上下界最大流
建图模型:
源点s,终点d。超级源点ss,超级终点dd。首先判断是否存在满足所有边上下界的可行流,方法可以转化成无源汇有上下界的可行流问题。怎么转换呢?
增设一条从d到s没有下界容量为无穷的边,那么原图就变成了一个无源汇的循环流图。接下来的事情一样,超级源点ss连i(du[i]>0),i连超级汇点(du[i]<0),
对(ss,dd)进行一次最大流,当maxflow等于所有(du[]>0)之和时,有可行流,否则没有。
当有可行流时,删除超级源点ss和超级终点dd,再对(s,d)进行一次最大流,此时得到的maxflow则为题目的解。为什么呢?因为第一次maxflow()只是求得所有满足下界的流量,而残留网络(s,d)路上还有许多自由流(没有和超级源点和超级汇点连接的边)没有流满,所有最终得到的maxflow=(第一次流满下界的流+第二次能流通的自由流)。
3.有源汇上下界最小流
建图模型:
du[i]表示i节点的入流之和与出流之和的差。
增设超级源点st和超级汇点sd,连(st,du[i](为正)),(-du[i](为负),sd)。 ///增设超级源点和超级汇点,因为网络中规定不能有弧指向st,也不能有流量流出sd
做一次maxflow()。
源点(Sd)和起点(St)连一条容量为oo的边。
再做一次maxflow()。
当且仅当所有附加弧满载时有可行流,最后答案为flow[(Sd->St)^1],St到Sd最大流就是Sd到St最小流。
总之,网络流的题目千变万化,多种算法、技巧之间相互嵌套,交叉,但却又有迹可循。只要善于思考,擅于总结,便一定能更上一层楼!
------------------分割线-----------------
我对网络流的理解仍旧是不深刻的,很多的地方依旧一知半懂,很多东西还是需要多理解的,这次的网络流小结便先总结到此吧。





















 4368
4368











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








