卷积神经网络（CNN）：从原理到实现

最新推荐文章于 2024-07-12 11:45:29 发布

MachineLP

最新推荐文章于 2024-07-12 11:45:29 发布

阅读量1w

点赞数 2

分类专栏： Deep learning 机器学习文章标签： CNN CNN原理 CNN实现

本文链接：https://blog.csdn.net/u014365862/article/details/54865609

版权

机器学习同时被 2 个专栏收录

292 篇文章 18 订阅

订阅专栏

Deep learning

175 篇文章 13 订阅

订阅专栏

MachineLP的Github（欢迎follow）：https://github.com/MachineLP

对照《CNN反向传播公式推导》就会很明白。

1.前言

（1）神经网络的缺陷

在神经网络一文中简单介绍了其原理，可以发现不同层之间是全连接的，当神经网络的深度、节点数变大，会导致过拟合、参数过多等问题。

（2）计算机视觉（图像）背景

通过抽取只依赖图像里小的子区域的局部特征，然后利用这些特征的信息就可以融合到后续处理阶段中，从而检测更高级的特征，最后产生图像整体的信息。
距离较近的像素的相关性要远大于距离较远像素的相关性。
对于图像的一个区域有用的局部特征可能对于图像的其他区域也有用，例如感兴趣的物体发生平移的情形。

2.卷积神经网络（CNN）特性

根据前言中的两方面，这里介绍卷积神经网络的两个特性。

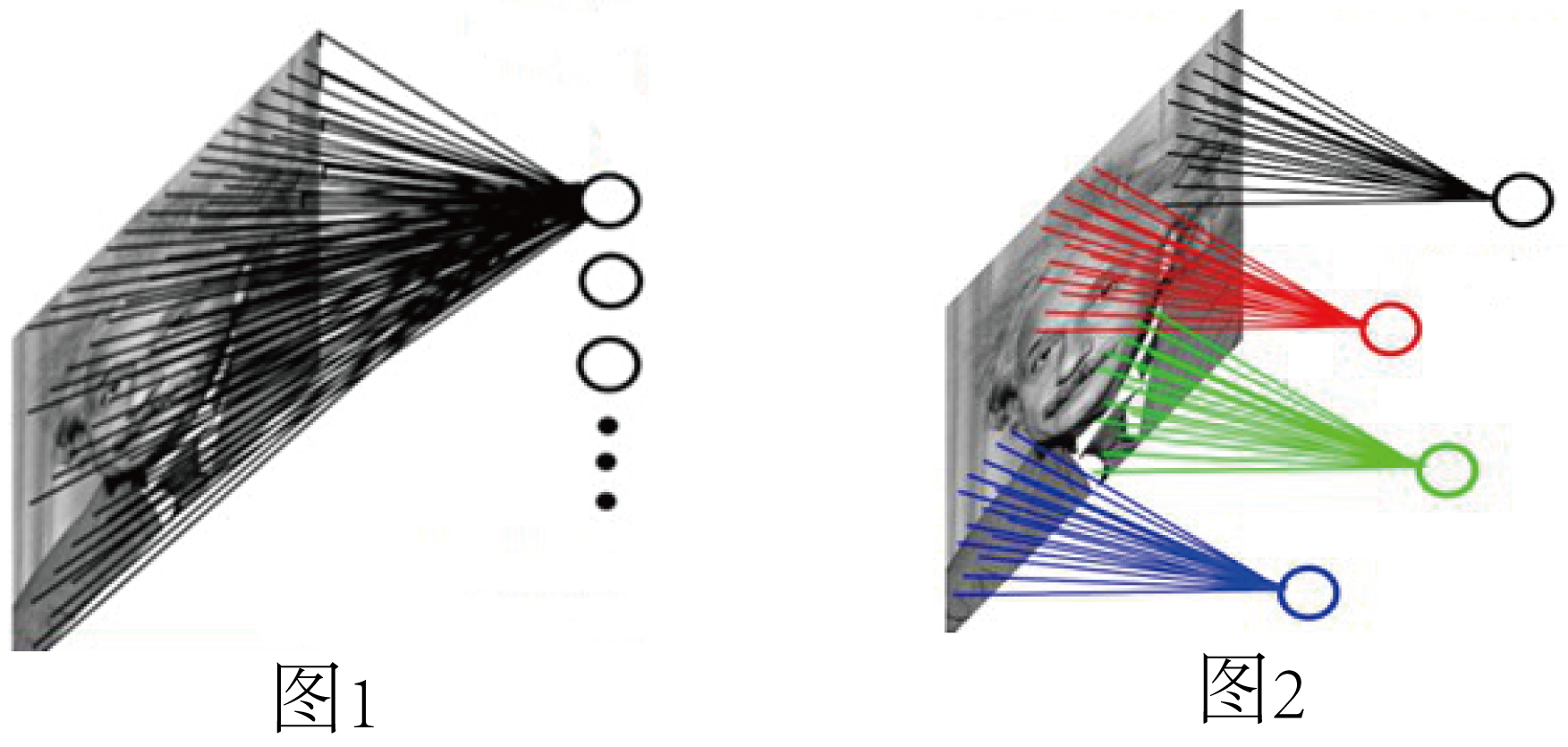
（1）局部感知

图1：全连接网络。如果L1层有1000×1000像素的图像，L2层有1000,000个隐层神经元，每个隐层神经元都连接L1层图像的每一个像素点，就有1000x1000x1000,000=10^12个连接，也就是10^12个权值参数。

图2：局部连接网络。L2层每一个节点与L1层节点同位置附近10×10的窗口相连接，则1百万个隐层神经元就只有100w乘以100，即10^8个参数。其权值连接个数比原来减少了四个数量级。

（2）权值共享

就图2来说，权值共享，不是说，所有的红色线标注的连接权值相同。而是说，每一个颜色的线都有一个红色线的权值与之相等，所以第二层的每个节点，其从上一层进行卷积的参数都是相同的。

图2中隐层的每一个神经元都连接10×10个图像区域，也就是说每一个神经元存在10×10=100个连接权值参数。如果我们每个神经元这100个参数是相同的？也就是说每个神经元用的是同一个卷积核去卷积图像。这样L1层我们就只有100个参数。但是这样，只提取了图像一种特征？如果需要提取不同的特征，就加多几种卷积核。所以假设我们加到100种卷积核，也就是1万个参数。

每种卷积核的参数不一样，表示它提出输入图像的不同特征（不同的边缘）。这样每种卷积核去卷积图像就得到对图像的不同特征的放映，我们称之为Feature Map，也就是特征图。

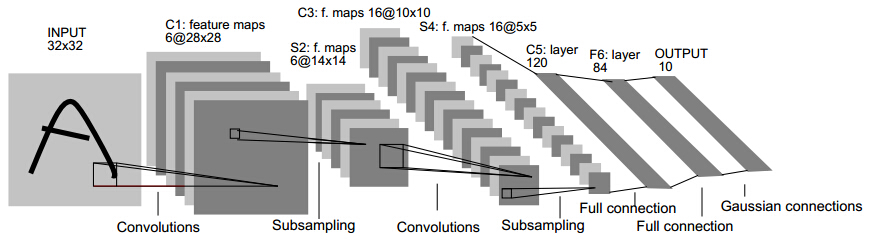
3.网络结构

以LeCun的LeNet-5为例，不包含输入，LeNet-5共有7层，每层都包含连接权值（可训练参数）。输入图像为32*32大小。我们先要明确一点：每个层有多个特征图，每个特征图通过一种卷积滤波器提取输入的一种特征，然后每个特征图有多个神经元。

C1、C3、C5是卷积层，S2、S4、S6是下采样层。利用图像局部相关性的原理，对图像进行下抽样，可以减少数据处理量同时保留有用信息。

图3

4.前向传播

在神经网络一文中已经详细介绍过全连接和激励层的前向传播过程，这里主要介绍卷积层、下采样（池化）层。

（1）卷积层

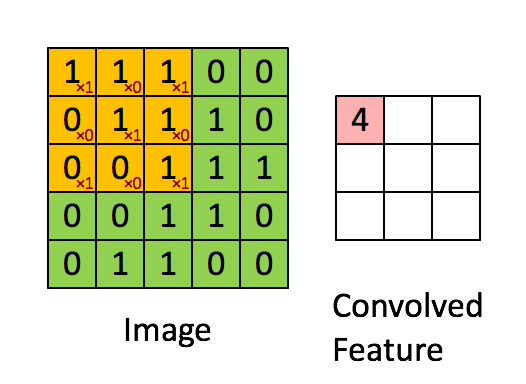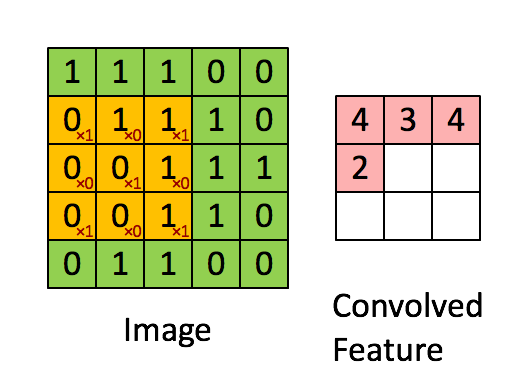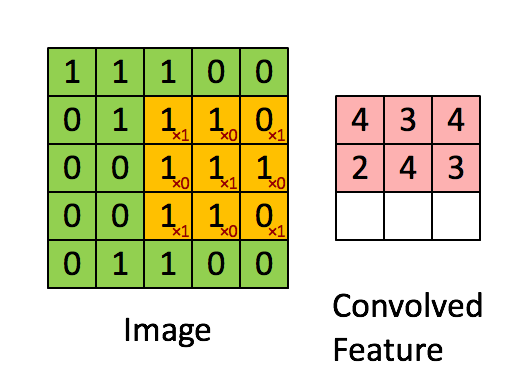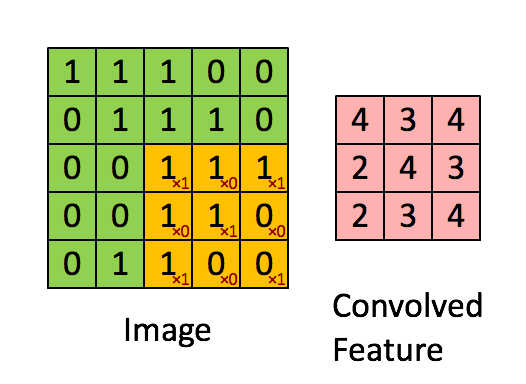
如图4所示，输入图片是一个5×5的图片，用一个3×3的卷积核对该图片进行卷积操作。本质上是一个点积操作。举例：1×1+0×1+1×1+0×0+1×1+0×1+1×0+0×0+1×1=4

图4

def conv2(X, k):
    x_row, x_col = X.shape
    k_row, k_col = k.shape
    ret_row, ret_col = x_row - k_row + 1, x_col - k_col + 1
    ret = np.empty((ret_row, ret_col))
    for y in range(ret_row):
        for x in range(ret_col):
            sub = X[y : y + k_row, x : x + k_col]
            ret[y,x] = np.sum(sub * k)
    return ret

class ConvLayer:
    def __init__(self, in_channel, out_channel, kernel_size):
        self.w = np.random.randn(in_channel, out_channel, kernel_size, kernel_size)
        self.b = np.zeros((out_channel))

    def _relu(self, x):
        x[x < 0] = 0

    def forward(self, in_data):
        # assume the first index is channel index
        in_channel, in_row, in_col = in_data.shape
        out_channel, kernel_row, kernel_col = self.w.shape[1], self.w.shape[2], self.w.shape[3]
        self.top_val = np.zeros((out_channel, in_row - kernel_row + 1, in_col - kernel_col + 1))
        for j in range(out_channel):
            for i in range(in_channel):
                self.top_val[j] += conv2(in_data[i], self.w[i, j])
            self.top_val[j] += self.b[j]
            self.top_val[j] = self._relu(self.topval[j])
        return self.top_val

（2）下采样（池化）层

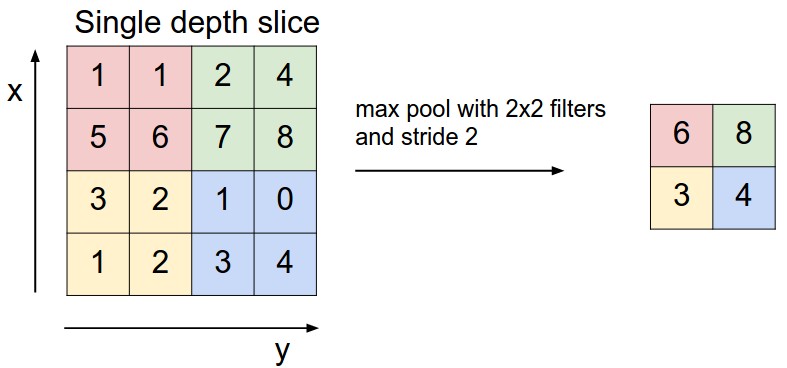
下采样，即池化，目的是减小特征图，池化规模一般为2×2。常用的池化方法有：

最大池化（Max Pooling）。如图5所示。
均值池化（Mean Pooling）。如图6所示。
高斯池化。借鉴高斯模糊的方法。
可训练池化。训练函数 ff ，接受4个点为输入，输出1个点。

图5

图6

class MaxPoolingLayer:
    def __init__(self, kernel_size, name='MaxPool'):
        self.kernel_size = kernel_size

    def forward(self, in_data):
        in_batch, in_channel, in_row, in_col = in_data.shape
        k = self.kernel_size
        out_row = in_row / k + (1 if in_row % k != 0 else 0)
        out_col = in_col / k + (1 if in_col % k != 0 else 0)

        self.flag = np.zeros_like(in_data)
        ret = np.empty((in_batch, in_channel, out_row, out_col))
        for b_id in range(in_batch):
            for c in range(in_channel):
                for oy in range(out_row):
                    for ox in range(out_col):
                        height = k if (oy + 1) * k <= in_row else in_row - oy * k
                        width = k if (ox + 1) * k <= in_col else in_col - ox * k
                        idx = np.argmax(in_data[b_id, c, oy * k: oy * k + height, ox * k: ox * k + width])
                        offset_r = idx / width
                        offset_c = idx % width
                        self.flag[b_id, c, oy * k + offset_r, ox * k + offset_c] = 1                        
                        ret[b_id, c, oy, ox] = in_data[b_id, c, oy * k + offset_r, ox * k + offset_c]
        return ret

5.后向传播

在神经网络一文中已经详细介绍过全连接和激励层的后向传播过程，这里主要介绍卷积层、下采样（池化）层。

（1）卷积层

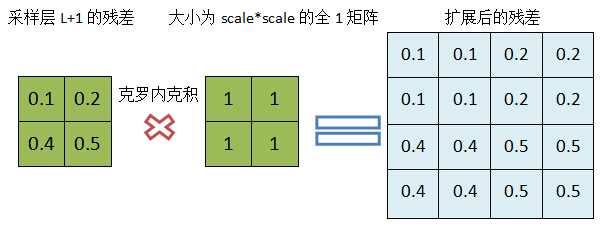
当一个卷积层L的下一层(L+1)为采样层，并假设我们已经计算得到了采样层的残差，现在计算该卷积层的残差。从最上面的网络结构图我们知道，采样层（L+1）的map大小是卷积层L的1/（scale*scale），以scale=2为例，但这两层的map个数是一样的，卷积层L的某个map中的4个单元与L+1层对应map的一个单元关联，可以对采样层的残差与一个scale*scale的全1矩阵进行克罗内克积进行扩充，使得采样层的残差的维度与上一层的输出map的维度一致。

扩展过程：

图7

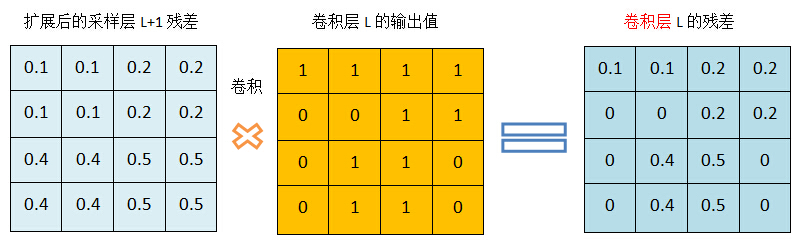
利用卷积计算卷积层的残差：

图8

def backward(self, residual):
    in_channel, out_channel, kernel_size = self.w.shape
    in_batch = residual.shape[0]
    # gradient_b        
    self.gradient_b = residual.sum(axis=3).sum(axis=2).sum(axis=0) / self.batch_size
    # gradient_w
    self.gradient_w = np.zeros_like(self.w)
    for b_id in range(in_batch):
        for i in range(in_channel):
            for o in range(out_channel):
                self.gradient_w[i, o] += conv2(self.bottom_val[b_id], residual[o])
    self.gradient_w /= self.batch_size
    # gradient_x
    gradient_x = np.zeros_like(self.bottom_val)
    for b_id in range(in_batch):
        for i in range(in_channel):
            for o in range(out_channel):
                gradient_x[b_id, i] += conv2(padding(residual, kernel_size - 1), rot180(self.w[i, o]))
    gradient_x /= self.batch_size
    # update
    self.prev_gradient_w = self.prev_gradient_w * self.momentum - self.gradient_w
    self.w += self.lr * self.prev_gradient_w
    self.prev_gradient_b = self.prev_gradient_b * self.momentum - self.gradient_b
    self.b += self.lr * self.prev_gradient_b
    return gradient_x

（2）下采样（池化）层

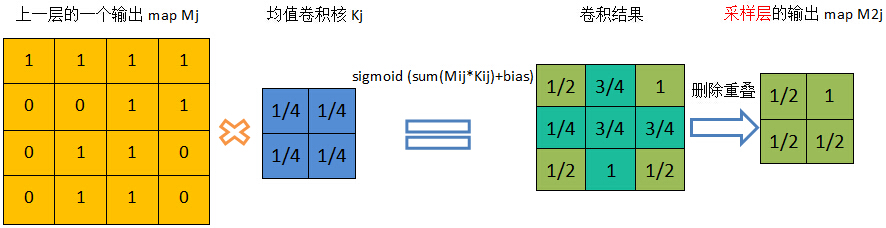
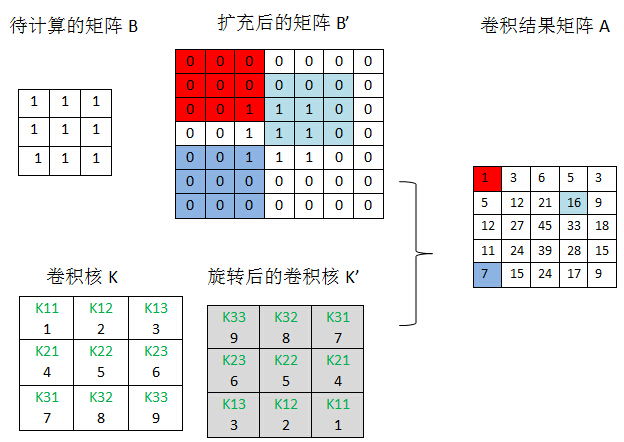
当某个采样层L的下一层是卷积层(L+1)，并假设我们已经计算出L+1层的残差，现在计算L层的残差。采样层到卷积层直接的连接是有权重和偏置参数的，因此不像卷积层到采样层那样简单。现再假设L层第j个map Mj与L+1层的M2j关联，按照BP的原理，L层的残差Dj是L+1层残差D2j的加权和，但是这里的困难在于，我们很难理清M2j的那些单元通过哪些权重与Mj的哪些单元关联，这里需要两个小的变换（rot180°和padding）：

rot180°：旋转：表示对矩阵进行180度旋转（可通过行对称交换和列对称交换完成）

def rot180(in_data):
    ret = in_data.copy()
    yEnd = ret.shape[0] - 1
    xEnd = ret.shape[1] - 1
    for y in range(ret.shape[0] / 2):
        for x in range(ret.shape[1]):
            ret[yEnd - y][x] = ret[y][x]
    for y in range(ret.shape[0]):
        for x in range(ret.shape[1] / 2):
            ret[y][xEnd - x] = ret[y][x]
    return ret

padding:扩充

def padding(in_data, size):
    cur_r, cur_w = in_data.shape[0], in_data.shape[1]
    new_r = cur_r + size * 2
    new_w = cur_w + size * 2
    ret = np.zeros((new_r, new_w))
    ret[size:cur_r + size, size:cur_w+size] = in_data
    return ret

图9

6.核心代码（demo版）

import numpy as np
import sys

def conv2(X, k):
    # as a demo code, here we ignore the shape check
    x_row, x_col = X.shape
    k_row, k_col = k.shape
    ret_row, ret_col = x_row - k_row + 1, x_col - k_col + 1
    ret = np.empty((ret_row, ret_col))
    for y in range(ret_row):
        for x in range(ret_col):
            sub = X[y : y + k_row, x : x + k_col]
            ret[y,x] = np.sum(sub * k)
    return ret

def rot180(in_data):
    ret = in_data.copy()
    yEnd = ret.shape[0] - 1
    xEnd = ret.shape[1] - 1
    for y in range(ret.shape[0] / 2):
        for x in range(ret.shape[1]):
            ret[yEnd - y][x] = ret[y][x]
    for y in range(ret.shape[0]):
        for x in range(ret.shape[1] / 2):
            ret[y][xEnd - x] = ret[y][x]
    return ret

def padding(in_data, size):
    cur_r, cur_w = in_data.shape[0], in_data.shape[1]
    new_r = cur_r + size * 2
    new_w = cur_w + size * 2
    ret = np.zeros((new_r, new_w))
    ret[size:cur_r + size, size:cur_w+size] = in_data
    return ret

def discreterize(in_data, size):
    num = in_data.shape[0]
    ret = np.zeros((num, size))
    for i, idx in enumerate(in_data):
        ret[i, idx] = 1
    return ret

class ConvLayer:
    def __init__(self, in_channel, out_channel, kernel_size, lr=0.01, momentum=0.9, name='Conv'):
        self.w = np.random.randn(in_channel, out_channel, kernel_size, kernel_size)
        self.b = np.zeros((out_channel))
        self.layer_name = name
        self.lr = lr
        self.momentum = momentum

        self.prev_gradient_w = np.zeros_like(self.w)
        self.prev_gradient_b = np.zeros_like(self.b)
    # def _relu(self, x):
    #     x[x < 0] = 0
    #     return x
    def forward(self, in_data):
        # assume the first index is channel index
        print 'conv forward:' + str(in_data.shape)
        in_batch, in_channel, in_row, in_col = in_data.shape
        out_channel, kernel_size = self.w.shape[1], self.w.shape[2]
        self.top_val = np.zeros((in_batch, out_channel, in_row - kernel_size + 1, in_col - kernel_size + 1))
        self.bottom_val = in_data

        for b_id in range(in_batch):
            for o in range(out_channel):
                for i in range(in_channel):
                    self.top_val[b_id, o] += conv2(in_data[b_id, i], self.w[i, o])
                self.top_val[b_id, o] += self.b[o]
        return self.top_val

    def backward(self, residual):
        in_channel, out_channel, kernel_size = self.w.shape
        in_batch = residual.shape[0]
        # gradient_b        
        self.gradient_b = residual.sum(axis=3).sum(axis=2).sum(axis=0) / self.batch_size
        # gradient_w
        self.gradient_w = np.zeros_like(self.w)
        for b_id in range(in_batch):
            for i in range(in_channel):
                for o in range(out_channel):
                    self.gradient_w[i, o] += conv2(self.bottom_val[b_id], residual[o])
        self.gradient_w /= self.batch_size
        # gradient_x
        gradient_x = np.zeros_like(self.bottom_val)
        for b_id in range(in_batch):
            for i in range(in_channel):
                for o in range(out_channel):
                    gradient_x[b_id, i] += conv2(padding(residual, kernel_size - 1), rot180(self.w[i, o]))
        gradient_x /= self.batch_size
        # update
        self.prev_gradient_w = self.prev_gradient_w * self.momentum - self.gradient_w
        self.w += self.lr * self.prev_gradient_w
        self.prev_gradient_b = self.prev_gradient_b * self.momentum - self.gradient_b
        self.b += self.lr * self.prev_gradient_b
        return gradient_x

class FCLayer:
    def __init__(self, in_num, out_num, lr = 0.01, momentum=0.9):
        self._in_num = in_num
        self._out_num = out_num
        self.w = np.random.randn(in_num, out_num)
        self.b = np.zeros((out_num, 1))
        self.lr = lr
        self.momentum = momentum
        self.prev_grad_w = np.zeros_like(self.w)
        self.prev_grad_b = np.zeros_like(self.b)
    # def _sigmoid(self, in_data):
    #     return 1 / (1 + np.exp(-in_data))
    def forward(self, in_data):
        print 'fc forward=' + str(in_data.shape)
        self.topVal = np.dot(self.w.T, in_data) + self.b
        self.bottomVal = in_data
        return self.topVal
    def backward(self, loss):
        batch_size = loss.shape[0]

        # residual_z = loss * self.topVal * (1 - self.topVal)
        grad_w = np.dot(self.bottomVal, loss.T) / batch_size
        grad_b = np.sum(loss) / batch_size
        residual_x = np.dot(self.w, loss)
        self.prev_grad_w = self.prev_grad_w * momentum - grad_w
        self.prev_grad_b = self.prev_grad_b * momentum - grad_b
        self.w -= self.lr * self.prev_grad_w
        self.b -= self.lr * self.prev_grad_b
        return residual_x

class ReLULayer:
    def __init__(self, name='ReLU'):
        pass

    def forward(self, in_data):
        self.top_val = in_data
        ret = in_data.copy()
        ret[ret < 0] = 0
        return ret
    def backward(self, residual):
        gradient_x = residual.copy()
        gradient_x[self.top_val < 0] = 0
        return gradient_x

class MaxPoolingLayer:
    def __init__(self, kernel_size, name='MaxPool'):
        self.kernel_size = kernel_size

    def forward(self, in_data):
        in_batch, in_channel, in_row, in_col = in_data.shape
        k = self.kernel_size
        out_row = in_row / k + (1 if in_row % k != 0 else 0)
        out_col = in_col / k + (1 if in_col % k != 0 else 0)

        self.flag = np.zeros_like(in_data)
        ret = np.empty((in_batch, in_channel, out_row, out_col))
        for b_id in range(in_batch):
            for c in range(in_channel):
                for oy in range(out_row):
                    for ox in range(out_col):
                        height = k if (oy + 1) * k <= in_row else in_row - oy * k
                        width = k if (ox + 1) * k <= in_col else in_col - ox * k
                        idx = np.argmax(in_data[b_id, c, oy * k: oy * k + height, ox * k: ox * k + width])
                        offset_r = idx / width
                        offset_c = idx % width
                        self.flag[b_id, c, oy * k + offset_r, ox * k + offset_c] = 1                        
                        ret[b_id, c, oy, ox] = in_data[b_id, c, oy * k + offset_r, ox * k + offset_c]
        return ret
    def backward(self, residual):
        in_batch, in_channel, in_row, in_col = self.flag
        k = self.kernel_size
        out_row, out_col = residual.shape[2], residual.shape[3]

        gradient_x = np.zeros_like(self.flag)
        for b_id in range(in_batch):
            for c in range(in_channel):
                for oy in range(out_row):
                    for ox in range(out_col):
                        height = k if (oy + 1) * k <= in_row else in_row - oy * k
                        width = k if (ox + 1) * k <= in_col else in_col - ox * k
                        gradient_x[b_id, c, oy * k + offset_r, ox * k + offset_c] = residual[b_id, c, oy, ox]
        gradient_x[self.flag == 0] = 0
        return gradient_x

class FlattenLayer:
    def __init__(self, name='Flatten'):
        pass
    def forward(self, in_data):
        self.in_batch, self.in_channel, self.r, self.c = in_data.shape
        return in_data.reshape(self.in_batch, self.in_channel * self.r * self.c)
    def backward(self, residual):
        return residual.reshape(self.in_batch, self.in_channel, self.r, self.c)

class SoftmaxLayer:
    def __init__(self, name='Softmax'):
        pass
    def forward(self, in_data):
        exp_out = np.exp(in_data)
        self.top_val = exp_out / np.sum(exp_out, axis=1)
        return self.top_val
    def backward(self, residual):
        return self.top_val - residual

class Net:
    def __init__(self):
        self.layers = []
    def addLayer(self, layer):
        self.layers.append(layer)
    def train(self, trainData, trainLabel, validData, validLabel, batch_size, iteration):
        train_num = trainData.shape[0]
        for iter in range(iteration):
            print 'iter=' + str(iter)
            for batch_iter in range(0, train_num, batch_size):
                if batch_iter + batch_size < train_num:
                    self.train_inner(trainData[batch_iter: batch_iter + batch_size],
                        trainLabel[batch_iter: batch_iter + batch_size])
                else:
                    self.train_inner(trainData[batch_iter: train_num],
                        trainLabel[batch_iter: train_num])
            print "eval=" + str(self.eval(validData, validLabel))
    def train_inner(self, data, label):
        lay_num = len(self.layers)
        in_data = data
        for i in range(lay_num):
            out_data = self.layers[i].forward(in_data)
            in_data = out_data
        residual_in = label
        for i in range(0, lay_num, -1):
            residual_out = self.layers[i].backward(residual_in)
            residual_in = residual_out
    def eval(self, data, label):
        lay_num = len(self.layers)
        in_data = data
        for i in range(lay_num):
            out_data = self.layers[i].forward(in_data)
            in_data = out_data
        out_idx = np.argmax(in_data, axis=1)
        label_idx = np.argmax(label, axis=1)
        return np.sum(out_idx == label_idx) / float(out_idx.shape[0])