花了一天时间把一直以来的“最大子序列”、“最大递增子序列“、”最大公共子序列“、“最长公共子串”等问题总结了一下。其中参考了若干博文，都备注引用。
首先子序列是指一个一个序列中，由若个数（字母）组成，然后从中任意删掉几个数（字母），保留剩下的数（字母）构成了一个序列，即称子序列。（或者从一个序列中，任意选取若干数或字符，按照这些数或字符原来的排序组成新的序列，即称子序列）
子串是指在一个字符串中任意选取连续的一段字符串，即称子串。
1首先看一下 最大子序列。
最大子序列是要找出由数组成的一维数组中和最大的连续子序列。比如{5,-3,4,2}的最大子序列就是 {5,-3,4,2}，它的和是8,达到最大；而 {5,-6,4,2}的最大子序列是{4,2}，它的和是6。你已经看出来了，找最大子序列的方法很简单，只要前i项的和还没有小于0那么子序列就一直向后扩展，否则丢弃之前的子序列开始新的子序列，同时我们要记下各个子序列的和，最后找到和最大的子序列。
int maxSubSum(const vector<int> & arr,int &begin,int &end){
int maxSum=0;
int currSum=0;
int newbegin=0;
for(int i=0;i<arr.size();++i){
currSum+=arr[i];
if(currSum>maxSum){
maxSum=currSum;
begin=newbegin;
end=i;
}
if(currSum<0){
currSum=0;
newbegin=i+1;
}
}
return maxSum;
}最大子序列、最长递增子序列、最长公共子串、最长公共子序列、字符串编辑距离
上述这篇博客中关于“最长递增子序列”讲解的不太好，我自己重新查看了如下的博客，讲解“最长递增子序列”的内容比较好。
2 最长递增子序列
最长递增子序列问题的描述：设L=<a1,a2,…,an>是n个不同的实数的序列，L的递增子序列是这样一个子序列Lin=<aK1,ak2,…,akm>，其中k1<k2<…<km且aK1<ak2<…<akm。求最大的m值。
设f(i)表示L中以ai为末元素的最长递增子序列的长度。则有如下的递推方程：
这个递推方程的意思是，在求以ai为末元素的最长递增子序列时，找到所有序号在L前面且小于ai的元素aj，即j<i且aj<ai。如果这样的元素存在，那么对所有aj,都有一个以aj为末元素的最长递增子序列的长度f(j)，把其中最大的f(j)选出来，那么f(i)就等于最大的f(j)加上1，即以ai为末元素的最长递增子序列，等于以使f(j)最大的那个aj为末元素的递增子序列最末再加上ai；如果这样的元素不存在，那么ai自身构成一个长度为1的以ai为末元素的递增子序列。
public void lis(float[] L)
{
int n = L.length;
int[] f = new int[n];//用于存放f(i)值；
f[0]=1;//以第a1为末元素的最长递增子序列长度为1；
for(int i = 1;i<n;i++)//循环n-1次
{
f[i]=1;//f[i]的最小值为1；
for(int j=0;j<i;j++)//循环i 次
{
if(L[j]<L[i]&&f[j]>f[i]-1)
f[i]=f[j]+1;//更新f[i]的值。
}
}
System.out.println(f[n-1]);
}
3 重点来了，难点与考点基本都集中在”最长公共子序列“和”最长公共子串“。首先看 最长公共子序列。
必须推荐这篇博客，用动态规划思想解最长公共子序列问题，详细说明了解题方法和分析思路。动态规划解最长公共子序列问题
问题描述：字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij=yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。
考虑最长公共子序列问题如何分解成子问题，设A=“a0，a1，…，am-1”，B=“b0，b1，…，bn-1”，并Z=“z0，z1，…，zk-1”为它们的最长公共子序列。不难证明有以下性质：
（1） 如果am-1=bn-1，则zk-1=am-1=bn-1，且“z0，z1，…，zk-2”是“a0，a1，…，am-2”和“b0，b1，…，bn-2”的一个最长公共子序列；
（2） 如果am-1!=bn-1，则若zk-1!=am-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列；
（3） 如果am-1!=bn-1，则若zk-1!=bn-1，蕴涵“z0，z1，…，zk-1”是“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列。
这样，在找A和B的公共子序列时，如有am-1=bn-1，则进一步解决一个子问题，找“a0，a1，…，am-2”和“b0，b1，…，bm-2”的一个最长公共子序列；如果am-1!=bn-1，则要解决两个子问题，找出“a0，a1，…，am-2”和“b0，b1，…，bn-1”的一个最长公共子序列和找出“a0，a1，…，am-1”和“b0，b1，…，bn-2”的一个最长公共子序列，再取两者中较长者作为A和B的最长公共子序列。
求解：
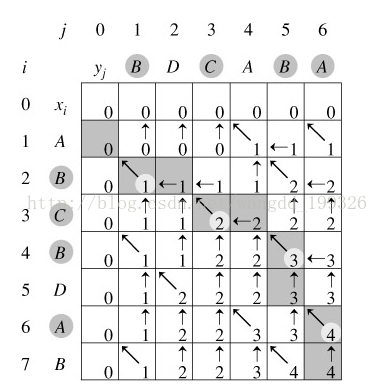
引进一个二维数组c[][]，用c[i][j]记录X[i]与Y[j] 的LCS 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。
我们是自底向上进行递推计算，那么在计算c[i,j]之前，c[i-1][j-1]，c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j]，就可以计算出c[i][j]。
问题的递归式写成：
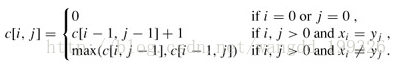
回溯输出最长公共子序列过程：
算法分析：
由于每次调用至少向上或向左（或向上向左同时）移动一步，故最多调用(m + n)次就会遇到i = 0或j = 0的情况，此时开始返回。返回时与递归调用时方向相反，步数相同，故算法时间复杂度为Θ(m + n)。
#include <stdio.h>
#include <string.h>
#define MAXLEN 100
void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN])
{
int i, j;
for(i = 0; i <= m; i++)
c[i][0] = 0;
for(j = 1; j <= n; j++)
c[0][j] = 0;
for(i = 1; i<= m; i++)
{
for(j = 1; j <= n; j++)
{
if(x[i-1] == y[j-1])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 0;
}
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 1;
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = -1;
}
}
}
}
void PrintLCS(int b[][MAXLEN], char *x, int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == 0)
{
PrintLCS(b, x, i-1, j-1);
printf("%c ", x[i-1]);
}
else if(b[i][j] == 1)
PrintLCS(b, x, i-1, j);
else
PrintLCS(b, x, i, j-1);
}
int main(int argc, char **argv)
{
char x[MAXLEN] = {"ABCBDAB"};
char y[MAXLEN] = {"BDCABA"};
int b[MAXLEN][MAXLEN];
int c[MAXLEN][MAXLEN];
int m, n;
m = strlen(x);
n = strlen(y);
LCSLength(x, y, m, n, c, b);
PrintLCS(b, x, m, n);
return 0;
}此处也推荐如下的几个博客关于对“最长公共子序列”的解法，思路与上述一样，但是具体算法实现上稍有不同。
4 对于“最长公共子串”的求解分析思路，推荐如右的博客。程序员面试100题之七：最长公共子字符串 这是大神hackbuteer1所撰写的两种思路，非常非常好！推荐看原博客。关于上述3种问题的关键部分，我已经基本总结好，需要的同学可以再点击链接进去详细查阅。对于该大神讲解“最长公共子序列”也可以观摩，学习。程序员面试100题之六：最长公共子序列
方法一：
Longest Common Substring和Longest Common Subsequence是有区别的
X = <a, b, c, f, b, c>
Y = <a, b, f, c, a, b>
X和Y的Longest Common Sequence为<a, b, c, b>，长度为4
X和Y的Longest Common Substring为 <a, b>长度为2
其实Substring问题是Subsequence问题的特殊情况，也是要找两个递增的下标序列
<i1, i2, ...ik> 和 <j1, j2, ..., jk>使
xi1 == yj1
xi2 == yj2
......
xik == yjk
与Subsequence问题不同的是，Substring问题不光要求下标序列是递增的，还要求每次
递增的增量为1， 即两个下标序列为：
<i, i+1, i+2, ..., i+k-1> 和 <j, j+1, j+2, ..., j+k-1>
类比Subquence问题的动态规划解法，Substring也可以用动态规划解决，令
c[i][j]表示Xi和Yi的最大Substring的长度，比如
X = <y, e, d, f>
Y = <y, e, k, f>
c[1][1] = 1
c[2][2] = 2
c[3][3] = 0
c[4][4] = 1
动态转移方程为：
如果xi == yj， 则 c[i][j] = c[i-1][j-1]+1
如果xi ! = yj, 那么c[i][j] = 0
最后求Longest Common Substring的长度等于
max{ c[i][j], 1<=i<=n， 1<=j<=m}
/**
找出两个字符串的最长公共连续子串的长度
** author :liuzhiwei
** data :2011-08-16
**/
#include "stdio.h"
#include "string.h"
#include "stdlib.h"
int longest_common_substring(char *str1, char *str2)
{
int i,j,k,len1,len2,max,x,y;
len1 = strlen(str1);
len2 = strlen(str2);
int **c = new int*[len1+1];
for(i = 0; i < len1+1; i++)
c[i] = new int[len2+1];
for(i = 0; i < len1+1; i++)
c[i][0]=0; //第0列都初始化为0
for(j = 0; j < len2+1; j++)
c[0][j]=0; //第0行都初始化为0
max = -1;
for(i = 1 ; i < len1+1 ; i++)
{
for(j = 1; j < len2+1; j++)
{
if(str1[i-1]==str2[j-1]) //只需要跟左上方的c[i-1][j-1]比较就可以了
c[i][j]=c[i-1][j-1]+1;
else //不连续的时候还要跟左边的c[i][j-1]、上边的c[i-1][j]值比较，这里不需要
c[i][j]=0;
if(c[i][j]>max)
{
max=c[i][j];
x=i;
y=j;
}
}
}
//输出公共子串
char s[1000];
k=max;
i=x-1,j=y-1;
s[k--]='\0';
while(i>=0 && j>=0)
{
if(str1[i]==str2[j])
{
s[k--]=str1[i];
i--;
j--;
}
else //只要有一个不相等，就说明相等的公共字符断了，不连续了
break;
}
printf("最长公共子串为：");
puts(s);
for(i = 0; i < len1+1; i++) //释放动态申请的二维数组
delete[] c[i];
delete[] c;
return max;
}
int main(void)
{
char str1[1000],str2[1000];
printf("请输入第一个字符串：");
gets(str1);
printf("请输入第二个字符串：");
gets(str2);
int len = longest_common_substring(str1, str2);
printf("最长公共连续子串的长度为：%d\n",len);
system("pause");
return 0;
}方法二：
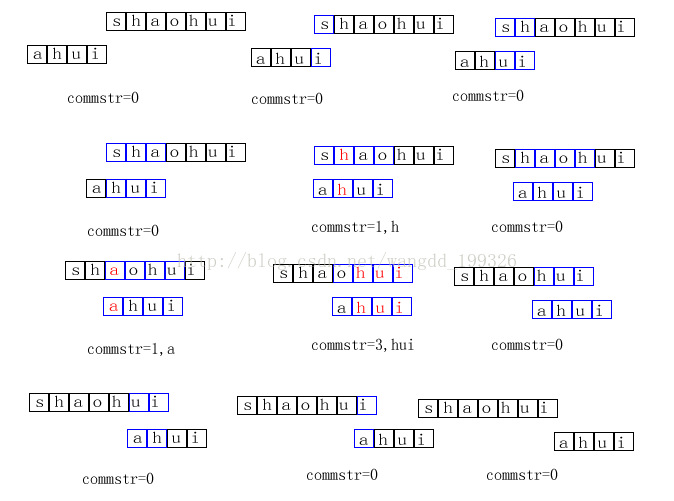
将字符串s1和s2分别写在两把直尺上面(我依然用s1，s2来表示这两把直尺)，然后将s1固定，s2的头部和s1的尾部对齐，然后逐渐移动直尺s2，比较重叠部分的字符串中的公共子串的长度，直到直尺s2移动到s1的头部。在这个过程中求得的最大长度就是s1、s2最大子串的长度。
下图是求解过程的图示（下图有点错误，应该是将s2从右往左移动），蓝色部分表示重叠的字符串，红色的部分表示重叠部分相同的子串
其中s1="shaohui"，s2="ahui"，最后求得的结果为3
/**
找出两个字符串的最长公共连续子串的长度
** author :liuzhiwei
** data :2011-08-16
**/
#include "stdio.h"
#include "string.h"
#include "stdlib.h"
int longest_common_substring(char *str1, char *str2)
{
int i,len1,len2,len,s1_start,s2_start,idx,curmax,max;
len1 = strlen(str1);
len2 = strlen(str2);
len = len1 + len2;
max = 0;
for(i = 0 ; i < len ; i++)
{
s1_start = s2_start = 0;
if(i < len1)
s1_start = len1 - i; //每次开始匹配的起始位置
else
s2_start = i - len1;
curmax = 0;
for(idx = 0 ; ( s1_start + idx < len1 ) && ( s2_start + idx < len2 ); idx++ )
{
if(str1[s1_start+idx]==str2[s2_start+idx])
curmax++;
else //只要有一个不相等，就说明相等的公共字符断了，不连续了，要保存curmax与max中的最大值，并将curmax重置为0
{
max = curmax > max ? curmax : max;
curmax = 0;
}
}
max = curmax > max ? curmax : max;
}
return max;
}
int main(void)
{
char str1[1000],str2[1000];
printf("请输入第一个字符串：");
gets(str1);
printf("请输入第二个字符串：");
gets(str2);
int len = longest_common_substring(str1, str2);
printf("最长公共连续子串的长度为：%d\n",len);
system("pause");
return 0;
}稍微改动一下，便可以输出公共子串了，就是要保存一下连续公共子串最后一个字符在其中一个字符串中的下标位置：
/**
找出两个字符串的最长公共连续子串的长度
** author :liuzhiwei
** data :2011-08-16
**/
#include "stdio.h"
#include "string.h"
#include "stdlib.h"
int longest_common_substring(char *str1, char *str2)
{
int i,k,len1,len2,len,s1_start,s2_start,idx,curmax,max;
len1 = strlen(str1);
len2 = strlen(str2);
len = len1 + len2;
max = 0;
for(i = 0 ; i < len ; i++)
{
s1_start = s2_start = 0;
if(i < len1)
s1_start = len1 - i; //每次开始匹配的起始位置
else
s2_start = i - len1;
curmax = 0;
for(idx = 0 ; ( s1_start + idx < len1 ) && ( s2_start + idx < len2 ); idx++ )
{
if(str1[s1_start+idx]==str2[s2_start+idx])
curmax++;
else //只要有一个不相等，就说明相等的公共字符断了，不连续了，要保存curmax与max中的最大值，并将curmax重置为0
{
//max = curmax > max ? curmax : max;
if(curmax > max)
{
max = curmax;
k = s1_start+idx-1; //保存连续子串长度增加时连续子串最后一个字符在str1字符串中的下标位置，便于输出公共连续子串
}
curmax = 0;
}
}
//max = curmax > max ? curmax : max;
if(curmax > max)
{
max = curmax;
k = s1_start+idx-1;
}
}
//输出公共子串
char s[1000];
for(i=0;i<max;i++)
s[i]=str1[k-max+1+i]; //公共字串在str1中的下标起始位置为k-max+1，结束位置为k
s[i]='\0';
printf("最长公共子串为：");
puts(s);
return max;
}
int main(void)
{
char str1[1000],str2[1000];
printf("请输入第一个字符串：");
gets(str1);
printf("请输入第二个字符串：");
gets(str2);
int len = longest_common_substring(str1, str2);
printf("最长公共连续子串的长度为：%d\n",len);
system("pause");
return 0;
}也有其他的一些博客，显然没有上述hack大神的思路详细又好，当然可以帮助我们来学习与理解。
1616
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
