HDU-1542-Atlantis-线段树+面积并（模板）

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1542

看了很短网上的博客，都写得很不错，我就是学着这篇博客写的，链接：http://www.cnblogs.com/ka200812/archive/2011/11/13/2247064.html

但是我觉得他们写的都不太详细，缺少步骤，像我这种菜鸟，就花了一上午，才搞定这一题；

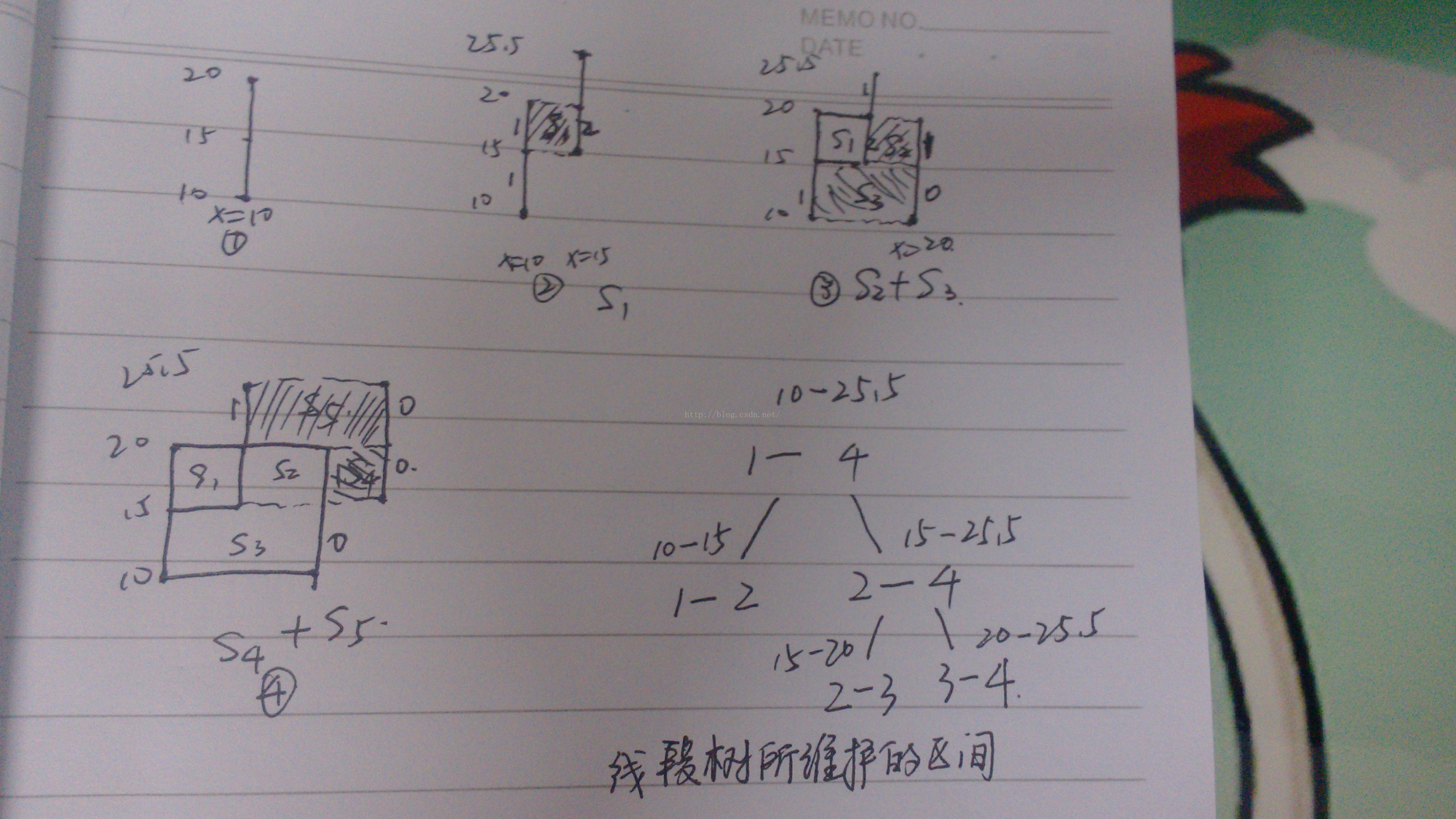
对于新学，我觉得还是有详细的步骤会更好的帮助理解；所以我就手画了一张步骤图，以及线段数怎么建的（orz,不会用那些高级的制图工具，so...）

首先建树，每个节点维护一个连续的区间；

总共4条竖向线段，所以共有4步插入查询，每次cover>0 说明有交面积，分步求；详细的请看图。。。

#include<iostream>
#include<string>
#include<cstdio>
#include<cstring>
#include<queue>
#include<map>
#include<cmath>
#include<stack>
#include<set>
#include<vector>
#include<algorithm>
#define LL long long
#define inf 1<<30
using namespace std;
const int N=205;
int n;
double y[N];
struct LINE     //  存储线段信息；
{
    double x;   //  该线段所在的位置；
    double y_up,y_down;     //  竖向线段的上下端点；
    int flag;
}line[N];
struct node
{
    double l,r;
    double x;       //  记录上一个横坐标位置，用于求面积；
    int cover;      //  记录覆盖的线段数；即同一方向的线段数；
    bool flag;      //  标记只有一个区间的节点，即10-15，15-20这是一个区间，我们将一个一个连续的区间离散化成一个节点；
}node[N<<2];
bool cmp(LINE a,LINE b)
{
    return a.x<b.x;
}
void build(int rt,int l,int r)      //  建树；
{
    node[rt].l=y[l];    //  维护区间；
    node[rt].r=y[r];
    node[rt].x=-1;
    node[rt].flag=false;
    node[rt].cover=0;
    if(l+1==r){             //  区间是连续的，即10-15,15-20;
        node[rt].flag=true; //  标记为节点；
        return;
    }
    int mid=(l+r)>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid,r);   //  同42行，所以此处mid不需要+1；
}
double Insert_query(int rt,double x,double l,double r,int flag) //  查询+更新x处（l,r）区间面积；
{
    if(l>=node[rt].r||r<=node[rt].l) return 0;  //  该方向节点不包含所要查询的区间；
    if(node[rt].flag){  //  找到只有一个区间的叶子节点；
        if(node[rt].cover>0){
            double pre=node[rt].x;
            double ans=(x-pre)*(node[rt].r-node[rt].l); //  计算面积；
            node[rt].x=x;       //  更新定位上一下x位置，便于下次计算面积；
            node[rt].cover+=flag;   //  更新覆盖的线段数；
            return ans;
        }else{
            node[rt].x=x;
            node[rt].cover+=flag;
            return 0;
        }
    }
    double ans1,ans2;
    ans1=Insert_query(rt<<1,x,l,r,flag);    //  直接往两个方向查，算有符合区间的面积；
    ans2=Insert_query(rt<<1|1,x,l,r,flag);  //  52行保证查询的可行性；
    return ans1+ans2;
}
int main()
{
    int Case=0;
    double x1,x2,y1,y2;
    while(~scanf("%d",&n)&&n){
        int cnt=-1;
        for(int i=0;i<n;i++){
            scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
            y[++cnt]=y1;
            line[cnt].x=x1;
            line[cnt].y_down=y1;
            line[cnt].y_up=y2;
            line[cnt].flag=1;   //  表示左边线段；
            y[++cnt]=y2;
            line[cnt].x=x2;
            line[cnt].y_down=y1;
            line[cnt].y_up=y2;
            line[cnt].flag=-1;  //  表示右边线段；
        }
        sort(y,y+cnt+1);        //  将所有高度由小到大排序，将区间建树表示；
        sort(line,line+cnt+1,cmp);      //  排序，返回坐标x靠左的点；
        build(1,0,cnt);
        double area=0;
        for(int i=0;i<=cnt;i++){
            area+=Insert_query(1,line[i].x,line[i].y_down,line[i].y_up,line[i].flag);
        }
        printf("Test case #%d\nTotal explored area: %.2lf\n\n",++Case,area);
    }
    return 0;
}