poj 1743 Musical Theme 较为简单的后缀数组+高度数组的应用

传送门：poj 1743 Musical Theme

题目大意

题意：有N(1 <= N <=20000)个音符的序列来表示一首乐曲，每个音符都是1..88范围内的整数，现在要找一个重复的主题。“主题”是整个音符序列的一个子串，它需要满足如下条件：
1. 长度至少为5个音符。
2. 在乐曲中重复出现。(可能经过转调，“转调”的意思是主题序列中每个音符都被加上或减去了同一个整数值)
3. 重复出现的同一主题不能有公共部分。

理解后缀数组

后缀数组就是比较难理解的一个算法。
在理解后缀数组和高度数组中，要理解下面几个变量：

要理解的变量

1. 字符串s表示输入的字符串也就是相当于原串
2. sa[i]这个数组里面存放的是后缀数组，不必存放的是后缀字符串，只要保存后缀字符串的起始位置就可以了 相当于”排第几的是谁”
3. rank[j]表示后缀数组起始位j的是第几小，相当于”你排第几”
4. height[i] 表示相邻的两个后缀的最长公共前缀
5. h[i] = height[rank[i]] 表示和他一个的sa[i-1]的最长公共前缀，h[i]就是按照没有排序的后缀来比较
6. suffix(i)就表示从i位置开始后缀数组
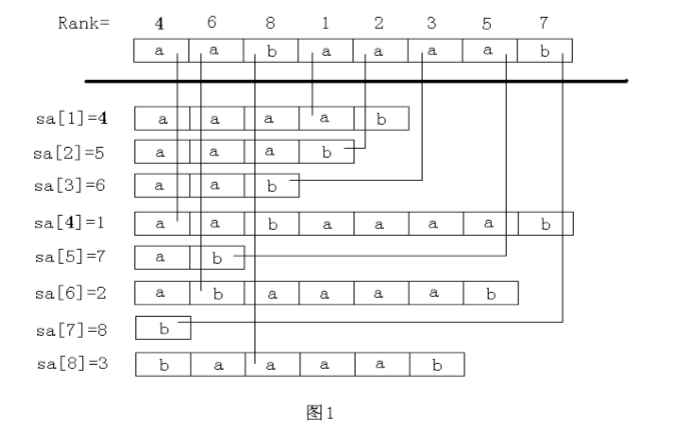
   下面举个例子[图1]来说明几个变量，以a = aabaaaab，sa的顺序如下
   
   rank数组的的排列是按照从上到下的顺序排列的，也就是rank[aaaab] = 1(rank[4] = 1)rank[aaab]=2(rank[5] = 2)
   下图就展示了什么是height数组
   
   下面在说一下最后一个变量h[i] = height[rank[i]]，比如当i==1的时候rank[1]=4也就是想当与h[1] = height[4] = 3,h[2] = height[6] = 2这样类推下去
   还要弄懂下面的几个关系：

要弄懂的关系

• .rank[sa[i]] = i 这个关系就说明了rank和sa这两个数组是相互逆运算的
• . height[i]等于sa[i]和sa[i-1]的最长公共前缀
• . h[i] = height[rank[i]] 这个有一个性质h[i]>=h[i-1]-1，在这里不做证明

几个原理

1. 怎么计算sa，倍增法

倍增算法的主要思想 ：对于一个后缀Suffix[i],如果想直接得到Rank比较困难，但是我们可以对每个字符开始的长度为2^k的字符串求出排名，k从0开始每次递增1(每递增1就成为一轮)，当2^k大于Len时，所得到的序列就是Rank，而SA也就知道了。O(logLen)枚举k
第k轮的rank是可以有第k-1轮的rank快速得到的，我们用s[i,len]表示从i位置开始长度为k的字符串子串，长度为len的字符串，我们可以把第k轮的s[i,len]看做s[i,2^(k-1)]和s[i+2^(k-1),2^(k-1)]拼凑而成的。为什么这么拼凑呢?因为长度为2^(k-1)的子串在上一轮已经遇到过了，理所当然的上一轮对应的rank也是计算出来的了如果每一轮都是这样的操作这就显然变为了第一关键字和第二关键字表大小了么！看下面这个经典的图就能理解：

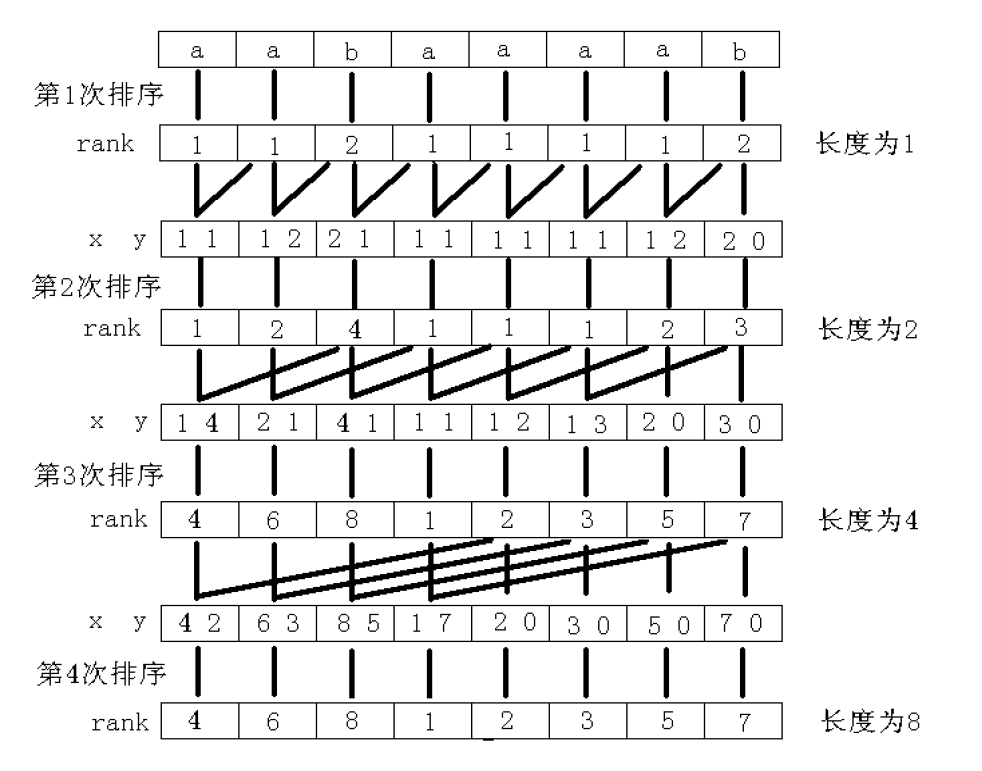
字符的比较和普通的整数比较是一样的。然后按照这种思路顺理成章就使用基数排序就能完成。
我们来看一下用代码怎么计算sa的

int cmp(int *r,int a,int b,int k)
{
    return r[a]==r[b]&&r[a+k]==r[b+k];
}

void getsa(int *r,int *sa,int n,int m)//n要包含末尾添加的0
{
    int i,j,p,*x=wa,*y=wb,*t;
    /*下面的四行是对长度为1的字符串进行排序*/
    for(i=0; i<m; i++)  wsf[i]=0;
    for(i=0; i<n; i++)  wsf[x[i]=r[i]]++;
    for(i=1; i<m; i++)  wsf[i]+=wsf[i-1];
    for(i=n-1; i>=0; i--)  sa[--wsf[x[i]]]=i;
    p=1;
    j=1;
    for(; p<n; j*=2,m=p)
    {
        for(p=0,i=n-j; i<n; i++)  y[p++]=i;
        for(i=0; i<n; i++)  if(sa[i]>=j)  y[p++]=sa[i]-j;
        for(i=0; i<n; i++)  wv[i]=x[y[i]];
        for(i=0; i<m; i++)  wsf[i]=0;
        for(i=0; i<n; i++)  wsf[wv[i]]++;
        for(i=1; i<m; i++)  wsf[i]+=wsf[i-1];
        for(i=n-1; i>=0; i--)  sa[--wsf[wv[i]]]=y[i];
        t=x;
        x=y;
        y=t;
        x[sa[0]]=0;
        for(p=1,i=1; i<n; i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
    }
}

怎么求高度数组

height数组：定义height[i]= suffix(sa[i-1])和 suffix(sa[i])的最长公
共前缀，也就是排名相邻的两个后缀的最长公共前缀，对于j和k如果有rank[j] < rank[k]则有下面的性质：

suffix(j) 和 suffix(k) 的 最 长 公 共 前 缀 为 height[rank[j]+1],height[rank[j]+2], height[rank[j]+3], … ,height[rank[k]]中的最小值.
以字符串为“aabaaaab”，求后缀“abaaaab”和后缀“aaab”的最长公
共前缀为例

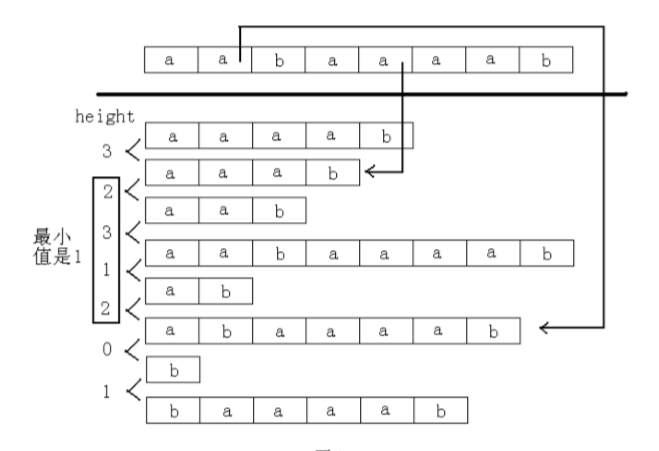
由于我们知道性质h[i]>=h[i-1]-1，按照这个性质计算h我们能把时间复杂度降低到o(n)
看代码是怎么得到高度数组的：

void getheight(int *r,int n)//n不保存最后的0
{
    int i,j,k=0;
    for(i=1; i<=n; i++) rank[sa[i]]=i;
    for(i=0; i<n; height[rank[i++]]=k)
        for(k?k--:0,j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++);
    return;
}

解题思路

在理解了上面的过程之后就大致的了解这个题目的思路了。
应该先二分答案，把题目变为判定性的问题：判断是否存在两个长度为k的子串是相同的，并且不重叠。解决这个问题还是要用到后缀数组和高度数组的结合，把sa分为若干组，其中每组的height的值不小于k，例如，字符串aabaaaab，当k=2的时候，后缀分为了四组，如下图所示：

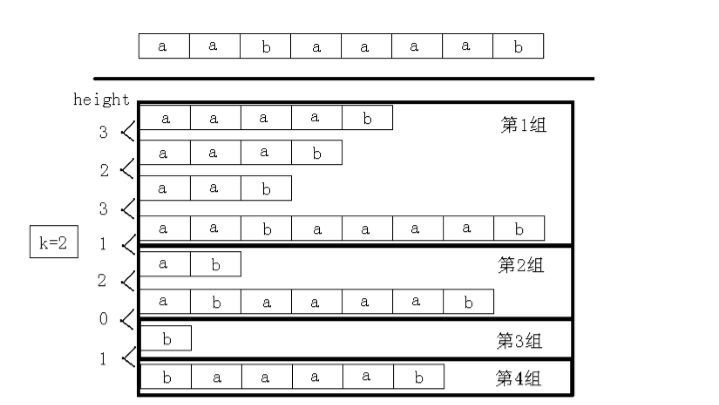
这就很容易看出来，有希望成为最长公共前缀不小于k的两个后缀一定在同一个组。然后只需要判断每个组的sa的最大值和最小值的差是不是不小于k，如果有一组满足则说明存在，否则不存在。对sa进行分组这个方法很重要

AC代码

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define N 20005
int wa[N],wb[N],wsf[N],wv[N],sa[N];
int rank[N],height[N],s[N],a[N],n;
char str1[N],str2[N];
//sa:字典序中排第i位的起始位置在str中第sa[i]
//rank:就是str第i个位置的后缀是在字典序排第几
//height：字典序排i和i-1的后缀的最长公共前缀
int cmp(int *r,int a,int b,int k)
{
    return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)//n要包含末尾添加的0
{
    int i,j,p,*x=wa,*y=wb,*t;
    for(i=0; i<m; i++)  wsf[i]=0;
    for(i=0; i<n; i++)  wsf[x[i]=r[i]]++;
    for(i=1; i<m; i++)  wsf[i]+=wsf[i-1];
    for(i=n-1; i>=0; i--)  sa[--wsf[x[i]]]=i;
    p=1;
    j=1;
    for(; p<n; j*=2,m=p)
    {
        for(p=0,i=n-j; i<n; i++)  y[p++]=i;
        for(i=0; i<n; i++)  if(sa[i]>=j)  y[p++]=sa[i]-j;
        for(i=0; i<n; i++)  wv[i]=x[y[i]];
        for(i=0; i<m; i++)  wsf[i]=0;
        for(i=0; i<n; i++)  wsf[wv[i]]++;
        for(i=1; i<m; i++)  wsf[i]+=wsf[i-1];
        for(i=n-1; i>=0; i--)  sa[--wsf[wv[i]]]=y[i];
        t=x;
        x=y;
        y=t;
        x[sa[0]]=0;
        for(p=1,i=1; i<n; i++)
            x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
    }
}
void getheight(int *r,int n)//n不保存最后的0
{
    int i,j,k=0;
    for(i=1; i<=n; i++) rank[sa[i]]=i;
    for(i=0; i<n; height[rank[i++]]=k)
        for(k?k--:0,j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++);
    return;
}
int ans;
int check(int k)
{
    int maxn,minn;
    maxn = minn = sa[1];
    for(int i = 2;i<=n;i++)
    {
        if(height[i]>=k && i<n)
        {
            minn = min(minn,sa[i]);
            maxn = max(maxn,sa[i]);
            continue;
        }
        if(maxn-minn>=k) return 1;
        maxn = minn = sa[i];
    }
    return 0;
}

void findAns()
{
    int l = 4,r = n;
    while(l<=r)
    {
        int mid = (l+r)/2;
        if(check(mid))
        {
            ans = mid;
            l=mid+1;
        }
        else r = mid-1;
    }
}

int main()
{
    int i,j,k;
    while((~scanf("%d",&n),n))
    {
        for(int i=0;i<n;i++) scanf("%d",&s[i]);
        for(int i=0;i<n-1;i++) s[i] = s[i+1]-s[i]+100;
        s[--n] = 0;
        getsa(s,sa,n+1,200);
        getheight(s,n);
        findAns();
        ans++;
        printf("%d\n",ans<5?0:ans);
    }
    return 0;
}