hdu 2050 折线分割平面

折线分割平面

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 20315    Accepted Submission(s): 13928

Problem Description

我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。

 

Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。

 

Output

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

 

Sample Input

  
  

   
   2
1
2
  
  

 

Sample Output

  
  

   
   2
7
  
  

 

Source

递推求解专题练习（For Beginner）

 

         对于递推问题 ，无非就是一个找规律，递推递推，顾名思义就是从前往后一次的推导。因此，递推问题，通常都能够有两种解法，一种是求其通项公式，某些的递推题能够求的它的递推公式，另外一种则是利用n-1项的或更多项推导第n项与其他项的关系，从而推导出递推公式。（显然后者更跟递推问题的本意符合，当然，后者的方法也是解答递推问题的主要方法。）

        本题的解答以上两种方法都是可以解答出来的。
 
        下面我们就来推导一下的他们的解题公式（先附上两条折线和三条折线的画法）

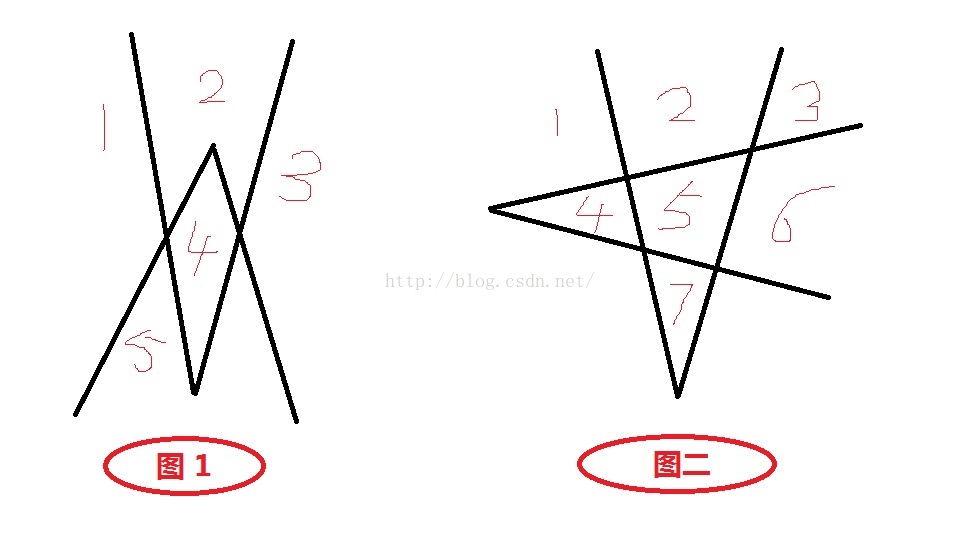
两条折线的画法（有多种画法，这里就画两种画法（最为对比推理），要求最多故需要的是图二的画法，也是原题给出的图）


以下是三条折线的画法（当然三条折线的画法有很多，这里就只给大家画出来正确的一种）

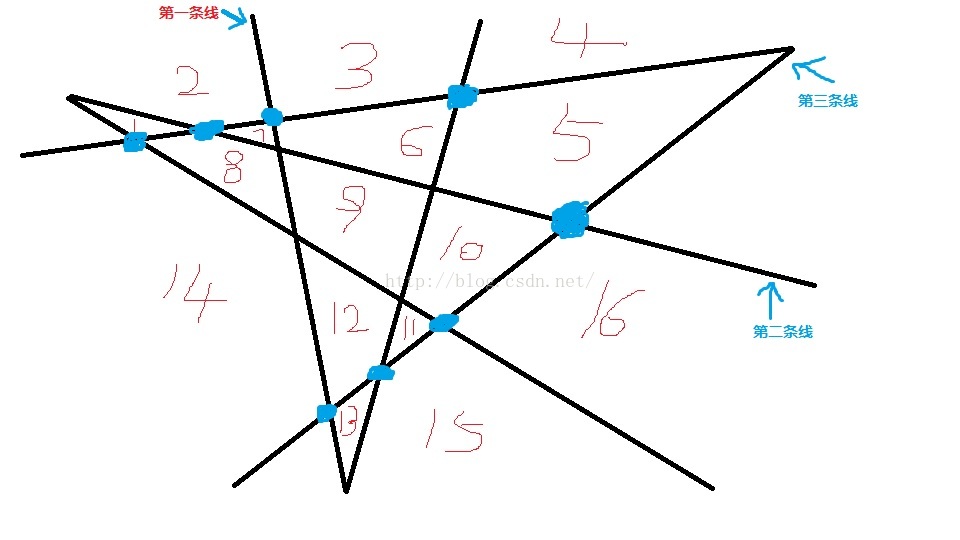
          这里我给大家推导以下递推公式的推导步骤：
         上面看到了两条折线 和三条折线的画法，我们先来考虑以下两条折线的画法，同样是两条折线为什么图二的就比图一的要多呢，我们这里仔细的分析以下两个图的不同，经过观察，不难发现，图二的交点比图一的交点多了两个，那是不是这个原因呢？回答是当然！那么问题又来了  交点的数目与分割的数量的增加有关系么？回答仍然是当然！那么交点数目与分割的数量到底有什么关系呢？我们再来看看图。
                    经过观察，你可以发现，如果在相邻的两个线段（或者射线）上任选取两个点，将这两点连线，那么原来的一个区域就会多被分割出来一个。所以每次所有的交点的之间的区域的数量的增加量就为 （交点的数量 - 1） ，那么交点的数量的增加量到底是多少呢？因为是一个折线（在这里我们可以将其近似考虑成两条直线），下面大家考虑以下“一条直线与n条直线能有几个交点?"答案必然是n个 ，所以当一个折线就可以形成2*n（这里的n表示的是n条直线，所以对于原题的来说一条折线与n条折线的交点数目就为 2*（2*n））个交点，所以第n条折线所有交点间比第n-1的折线的区域数量增加了4*（n-1） - 1 (交点的数量 - 1 )块，另外需要注意的是，这是一条折线，所以当与其他的线相交过后必然会在其两端都形成一条射线，这两条射线也是能够将区域分割开的，所以分割的增加量除了前面交点形成的增加量意外，还有这两个射线的增加的  2  块。
          
             所以就有f(n) = f(n-1) + 4 * (n-1) - 1 + 2;
              化简的  f(n) = (n-1) + 4 * n - 3;
            

      附上源代码：

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
	long long s[10050] = {1,2,7};
	for(int i = 3;i < 10001;i++)
	{
		s[i] = s[i-1] + 4 * i - 3;
	}
	int n;
	cin >> n;
	while(n--)
	{
		int a;
		cin >> a;
		cout << s[a] << endl;
	}
	return 0;
}

另外还有一种就是求其通项公式：

根据直线分平面可知，由交点决定了射线和线段的条数，进而决定了新增的区域数。当n-1条折线时，区域数为f（n-1）。为了使增加的区域最多，则折线的两边的线段要和n-1条折线的边，即2*（n-1）条线段相交。那么新增的线段数为4*（n-1），射线数为2。但要注意的是，折线本身相邻的两线段只能增加一个区域。

       

       故：f(n)=f(n-1)+4(n-1)+2-1

                      =f(n-1)+4(n-1)+1

                     =f(n-2)+4(n-2)+4(n-1)+2

                     ……

                     =f(1)+4+4*2+……+4(n-1)+(n-1)   

                     =2n^2-n+1

通项公式为：2 * n^2 - n + 1

      附上源代码：

 

#include <iostream>
using namespace std;

int main()
{
	int n, m;
	cin >>n;

	while(n--)
	{
		cin >>m;
		cout <<2*m*m - m + 1 <<endl;
	}
	return 0;
}