C++ 堆排序

最新推荐文章于 2024-09-03 13:49:44 发布
最新推荐文章于 2024-09-03 13:49:44 发布
阅读量2k 收藏 13
点赞数 3
分类专栏： C++ 算法思维和数据结构 文章标签： C++ 堆排序
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/emaste_r/article/details/7098285
版权

1.要看堆，先看完全二叉树


如果对第一节的完全二叉树不感兴趣，请用目录跳到第二节。


事实上，本人对二叉树的高度和深度一直搞不太清楚。

我发现没有一个统一的定义，连代码都不知道怎么写了，那我们定义：

（1）一颗完全二叉树层数从0开始计算，第 i 层最多有 2^i 个结点

（2）结点的高度：从本结点到叶子的最长简单下降路径边的数目

（3）基于第2点，空的完全二叉树高度为-1，只有根结点的高度为0（没有边），高度为k（k>=-1）的二叉树的最大结点2^(k+1) - 1

（4）具有n个结点的完全二叉树高度 ceil（ log2(n)+1）,ceil()是向下取整 

（5）树的深度：树的所有结点的最大层数（照这么定义，树的深度 == 根的高度，深度形容树，高度形容结点）



完全二叉树定义

（第一种）二叉树深度为H，结点数为N，它与一棵深度为H的满二叉树的【1..N】结点，唯一对应，这样的二叉树叫完全二叉树。

（第二种）二叉树的每一层除了最后一层都是满的，最后一层的结点连续集中在最左侧。

.


完全二叉树特点


能回到这些问题吗？
（1）想到完全二叉树，你会想到什么数据结构来描述它
（2）高度为h，那么每一层 最多有多少结点？总共 最多有多少结点？
（3）知道了父结点，怎么求孩子结点吗？
（4）知道了孩子结点，怎么求父结点吗？
（5）怎么立刻知道一个父结点是否拥有两个孩子结点？拥有一个孩子结点呢？
（6）怎么立刻确定一个结点是叶子结点呢？
如果你不懂，以上问题都是很简单的问题，只要你跟着以下几张图走，就明白了！
如果你懂，请跳过 第 1 大节！


（一）基于完全二叉树的特性，很明显地，我们用数组而不是链表来描述它

（二）高度为h，每一层有2^(h)个结点，总共最多有2^(h+1) - 1个结点

 

（三）知道父亲结点，求孩子结点？

如果父亲是i且2*i<=n（边界条件），那么左孩子就是2*i
如果孩子是i且2*i+1 <= n（边界条件），那么右孩子就是2*i+1
 

（四）知道孩子结点，求父亲结点？

i结点的父亲是i/2，取整，其中i>1（边界条件）
 

（五）立刻确定某父亲结点 i 拥有两个孩子？

  2*i+1 <= n
 

（六）立刻确定某结点为叶子结点？

 2*i > n

 

我们可以很明显的推导出来，叶子结点：[n/2],[n/2]+1,[n/2]+2,..,n          

(后面BuildMaxHeap()要用到哦~)



完全二叉树叶子结点数算法

n0 =  floor（n/2）
证明：
已知共有结点n，度为0的结点为n0（也就是叶结点），度为1的结点为n1，度为2的结点为n2
（1）n = n0+ n1+n2
（2）二叉树特性：入度 =出度（入的分支数 = 出的分支数） => n-1 = 2*n2 + 1* n1 + 0*n0
那么：n-1 = n0+n1+n2-1 = 2*n2 + n1
那么：n2 +1 = n0
（3）在完全二叉树中，n1的个数要么为0，要么为1
n = n0 + n2 + n1
   = n0 + n0-1 + 0 （ n0 + n0-1 +1）
   = 2*n0 -1 （2*n0）
那么 n0 = floor（n/2），floor() 向上取整



2.堆排序-一个时间复杂度为O(nlgn)的排序


为了方便以及可移植性，我们定义一个 CHeap类： 
class CHeap
{
public:
    CHeap(int heapSize):mHeapSize(heapSize)
    {
        mHeap = new int[heapSize];
        if(NULL != mHeap)
        {
            memset(mHeap,0,sizeof(int)*heapSize);
        }
    }

    ~CHeap()
    {
        delete[] mHeap;
    }

    void MaxHeapify(int i);
    void MaxHeapify_iteration(int i);
    void MaxHeapify_iteration_2(int i);
    void BuildMaxHeap();
    void HeapSort();

    inline void SetMHeapValue(int *a,int size)
    {
        for(int i=0; i<size;i++ )
        {
            mHeap[i] = a[i];
        }
    }
    inline int LeftChild(int i)
    {
        return (i<<1)+1;
    }
    inline int RightChild(int i)
    {
        return (i<<1)+2;
    }
    inline void Swap(int &a,int &b)
    {
        int tmp = a;
        a=b;
        b=tmp;
    }

public:
    int mHeapSize;
    int* mHeap;
};



MaxHeapify(int i)


功能：使以 i 为祖先的分支成为最大堆。 

void CHeap::MaxHeapify(int i)
{
    int left = LeftChild(i);
    int right = RightChild(i);
    int max = i;

    //父亲，左孩子，右孩子 三者取MAX
    if(left < mHeapSize && mHeap[i] < mHeap[left]) { max = left;}
    if(right < mHeapSize && mHeap[max] < mHeap[right]) { max = right;}
    //如果父亲没有孩子大，就和孩子换
    if(max != i)
    {
        Swap(mHeap[max],mHeap[i]);
        //交换后可能破坏了最大堆性质，还要对交换后的父亲结点MaxHeapify
        MaxHeapify(max);
    }
}

解读：
（1）在二叉树中像这种从上到下的算法，很明显时间复杂度就是lg(n)。
（2）就是保证父亲比两个孩子都大，小了就交换，换完再次确保被换下来的父亲依旧满足这个规则即可。

重点解读：
（1）T(n)时间复杂度，可以分解为规模为T(2n/3)的子情况+执行必要代码的Θ(1)
（2）为什么是2n/3的子情况呢？因为最后一层刚刚半满，子情况中结点数为总的结点数的2/3
（3）T(n) = T(2n/3) +Θ1 
（4）递归式的主方法可得：g(n) = n^(log2/3(1)) = n^0 = 1 = f(n)  
           T(n) = O(lgn) 


BuildMaxHeap()


功能：建立最大堆。 

void CHeap::BuildMaxHeap()
{
    for(int i = mHeapSize/2 -1  ; i >= 0;i--)
    {
        MaxHeapify(i);
    }
}

解读：
（1）我们分析过了，叶子结点：[n/2],[n/2]+1,[n/2]+2,...n
（2）我们在建立最大堆的时候，要从有孩子的父结点开始从底往上建立！
（3）单个叶子结点因为没有孩子而被默认为最大堆了（想想看，建堆的时候有一个过程：父，左，右三者取大）

重点解读：
（1）根据0x13-1节的重点解读，我们知道MaxHeapify()的时间复杂度为 O(lgn)
（2）明显，BuildMaxHeap() 时间复杂度为 nlgn，但是《算法导论》说，呵呵，可以逼近
（3） 然后用了个级数的积分和微分公式，逼近成了O(n)



HeapSort()


功能：堆排序。 

void CHeap::HeapSort()
{
    BuildMaxHeap();
    for(int i = mHeapSize-1; i >= 1 ; i--)
    {
        Swap(mHeap[i],mHeap[0]);
        mHeapSize --;
        MaxHeapify(0);
    }
}

解读：
（1）BuildMaxHeap()建立最大堆之后，根元素就是最大的！我们取出来，放到堆尾巴
（2）放完根元素后，堆的规模减1
           因为本来的堆尾跑到了堆的根，我们要来一次MaxHeapify(0);保持堆的性质（爸爸比孩子大）
（3）直到堆的规模为1的时候结束（留下的最后一个不用排）

重点解读：
（1）BuildMaxHeap() 时间复杂度为O(n)
（2）MaxHeapify() 时间复杂度为O(lgn)，加个循环：O(nlgn)
（3）加起来是O(n) + O(nlgn) = O(nlgn)



迭代版MaxHeapify()

实际上，迭代版本避免了进出函数所费的时间，比递归版本要高效些。
我们可以用循环来代替递归： 
void CHeap::MaxHeapify_iteration(int i)
{
    int left = LeftChild(i);
    int right = RightChild(i);
    int max = i;
    if(left < mHeapSize && mHeap[i] < mHeap[left]) { max = left;}
    if(right < mHeapSize && mHeap[max] < mHeap[right]) { max = right;}
    //和递归版本区别在置换后对"堆结构的破坏"的修复

    while(max != i)
    {
        swap(mHeap[i], mHeap[max]);
        i = max;
        left = LeftChild(i);
        right = RightChild(i);
        if(left < mHeapSize && mHeap[left] > mHeap[i])  {  max = left;}
        if(right < mHeapSize && mHeap[right] > mHeap[max])  {  max = right;}
    }
}

算法导论给出的迭代版： 
void CHeap::MaxHeapify_iteration_2(int i)
{
    int left = LeftChild(i);
    int right = RightChild(i);
    while(left < mHeapSize)
    {
        int max = i;
        if(left < mHeapSize && mHeap[left] > mHeap[i]){ max = left;}
        if(right < mHeapSize && mHeap[right] > mHeap[max]){max = right;}
        if(max != i)
        {
            Swap(mHeap[max],mHeap[i]);

            i = max;
            left = LeftChild(i);
            right = RightChild(i);
        }
        else
            break;
    }
}


不稳定的排序


如果两个相同的值，排序后位置不变，则稳定。
否则，不稳定。
我们看看HeapSort()，为了方便说明，举个例子：
序列：39,27,36,27（用二叉树建立）


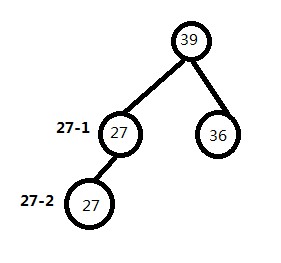
这是一个最大堆！为了方便，我们把第一个27标志位27_1，第二个27标志位27_2
（1）排序的时候把根元素39放到堆尾巴
（2）27_2会被提到根元素，进行一轮排序，27_2在与27_1比较的时候并不用调换位置
（3）轮到27输出的时候，27_2先于27_1输出

结论：堆排序是不稳定的排序！


编程应用


使用方法：


本人把代码放到一个CHeap.h文件中，使用方法是导入：#include"CHeap.h"
使用代码如： 
int size = 5;
CHeap heap(size);
int A[5]={3,21,1,51,42};
heap.SetMHeapValue(A,size);
heap.HeapSort();


导入CHeap.h


#ifndef CHEAP_H_INCLUDED
#define CHEAP_H_INCLUDED
#include <memory.h>
#include <string.h>
#include <iostream>

class CHeap
{
public:
    CHeap(int heapSize):mHeapSize(heapSize)
    {
        mHeap = new int[heapSize];
        if(NULL != mHeap)
        {
            memset(mHeap,0,sizeof(int)*heapSize);
        }
    }

    ~CHeap()
    {
        delete[] mHeap;
    }

    void MaxHeapify(int i);
    void MaxHeapify_iteration(int i);
    void MaxHeapify_iteration_2(int i);
    void BuildMaxHeap();
    void HeapSort();

    inline void SetMHeapValue(int *a,int size)
    {
        for(int i=0; i<size;i++ )
        {
            mHeap[i] = a[i];
        }
    }
    inline int LeftChild(int i)
    {
        return (i<<1)+1;
    }
    inline int RightChild(int i)
    {
        return (i<<1)+2;
    }
    inline void Swap(int &a,int &b)
    {
        int tmp = a;
        a=b;
        b=tmp;
    }

public:
    int mHeapSize;
    int* mHeap;
};

void CHeap::MaxHeapify(int i)
{
    int left = LeftChild(i);
    int right = RightChild(i);
    int max = i;

    //父亲，左孩子，右孩子 三者取MAX
    if(left < mHeapSize && mHeap[i] < mHeap[left]) { max = left;}
    if(right < mHeapSize && mHeap[max] < mHeap[right]) { max = right;}
    //如果父亲没有孩子大，就和孩子换
    if(max != i)
    {
        Swap(mHeap[max],mHeap[i]);
        //交换后可能破坏了最大堆性质，还要对交换后的父亲结点MaxHeapify
        MaxHeapify(max);
    }

}


void CHeap::MaxHeapify_iteration(int i)
{
    int left = LeftChild(i);
    int right = RightChild(i);
    int max = i;
    if(left < mHeapSize && mHeap[i] < mHeap[left]) { max = left;}
    if(right < mHeapSize && mHeap[max] < mHeap[right]) { max = right;}
    //和递归版本区别在置换后对"堆结构的破坏"的修复

    while(max != i)
    {
        Swap(mHeap[i], mHeap[max]);
        i = max;
        left = LeftChild(i);
        right = RightChild(i);
        if(left < mHeapSize && mHeap[left] > mHeap[i])  {  max = left;}
        if(right < mHeapSize && mHeap[right] > mHeap[max])  {  max = right;}
    }
}

//算法导论上给出的迭代版本
void CHeap::MaxHeapify_iteration_2(int i)
{
    int left = LeftChild(i);
    int right = RightChild(i);
    while(left < mHeapSize)
    {
        int max = i;
        if(left < mHeapSize && mHeap[left] > mHeap[i]){ max = left;}
        if(right < mHeapSize && mHeap[right] > mHeap[max]){max = right;}
        if(max != i)
        {
            Swap(mHeap[max],mHeap[i]);

            i = max;
            left = LeftChild(i);
            right = RightChild(i);
        }
        else
            break;
    }
}


void CHeap::BuildMaxHeap()
{
    for(int i = mHeapSize/2 -1  ; i >= 0;i--)
    {
        MaxHeapify(i);
    }
}

void CHeap::HeapSort()
{
    BuildMaxHeap();
    for(int i = mHeapSize-1; i >= 1 ; i--)
    {
        Swap(mHeap[i],mHeap[0]);
        mHeapSize --;
        MaxHeapify(0);
    }
}


#endif // CHEAP_H_INCLUDED


ouyangbro
关注
专栏目录
C++堆排序C++堆排序.zip
01-18
**C++堆排序详解** 堆排序是一种基于比较的排序算法，它的主要思想是利用数据结构中的堆特性来实现数组或序列的排序。在C++中，我们可以通过标准库中的`<algorithm>`头文件来实现堆排序，但更深入的理解和自定义...
C++堆排序算法的实现方法
12-26
本文实例讲述了C++实现堆排序算法的方法，相信对于大家学习数据结构与算法会起到一定的帮助作用。具体内容如下：  首先，由于堆排序算法说起来比较长，所以在这里单独讲一下。堆排序是一种树形选择排序方法，它的...
堆排序c++
weixin_39608351的博客
05-27 263
#include <iostream> #include <algorithm> using namespace std; void max_heapify(int arr[], int start, int end) { // 建立父節點指標和子節點指標 int dad = start; int son = dad * 2 + 1; w...
【C++】堆排序
Ljnoit
04-15 214
堆排序百科名片排序操作动图演示代码实现 百科名片 堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。 排序操作 在堆的数据结构中，堆中的最大值总是位于根节点（在优先队列中使用堆的话堆中的最小值位于根节点）。堆中定义以下几种操作： 最大堆调整（Max Heapify）：...
C++中堆排序详解
最新发布
qq_56740121的博客
09-03 249
堆（Heap）是一种特殊的完全二叉树结构，它通常被用作优先队列的实现，或者是在实现如堆排序这样的算法时用到。堆有两种主要的类型：最大堆（Max Heap）和最小堆（Min Heap）。完全二叉树：除了最后一层外，每一层都被完全填满，并且所有节点都尽可能地向左对齐。也就是说，除最后一层外，所有层均为满层。最后一层，所有节点的排布都要靠左，直至排满。（个人理解）。最大堆：每个父节点的值都大于其子节点的值。（所有父亲都比儿子大）根节点最大最小堆：每个父节点的值都小于其子节点的值。
堆排序(C++版)
weixin_46269257的博客
08-07 103
//堆排序->完全二叉树 //时间复杂度都是nlogn 空间复杂度是O(n) #include <iostream> #include <vector> using namespace std; void print(vector<int>& nums){ for(auto a: nums){ cout<<a<<" "; } cout<<endl; } //对每个节点做heap
C++——堆排序
Shirven
05-15 165
堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了 #include <iostream> #include <cstdlib> using namespace std;...
C++：堆排序
luzhongshan的博客
06-05 3243
目录 什么是堆排序： 堆排序步骤： 步骤一 、构造初始堆。将给定无序序列构造成一个大顶堆 步骤二 、将堆顶元素与末尾元素进行交换，使末尾元素最大。 最后结果： 再简单总结下堆排序的基本思路： 代码： 　堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。 什么是堆排序：...
C++堆排序实现算法
06-01
简单的堆排序算法：以定长数组为例，动态数组等可以以此类推
C++堆排序算法的实现
10-09
在C++中，堆排序可以通过创建一个最大堆（或最小堆）并反复调整堆来实现数组的排序。最大堆是一个完全二叉树，其中每个父节点的值都大于或等于其子节点的值。最小堆则相反，父节点的值小于或等于子节点的值。本文...
C++堆排序算法实例详解
08-29
C++堆排序算法实例详解 C++堆排序算法是基于完全二叉树结构的排序算法，它将数组看作是一个完全二叉树，然后通过调整节点的顺序来实现排序。下面将详细介绍C++堆排序算法的原理和实现。 一、堆排序算法的原理 堆...
堆排序（c++）
Kmp算法C语言简单实现
11-14 386
堆排序是选择排序的一种 堆排序只需要一个记录大小的辅助空间，每个待排序的记录只需要一个空间大小即可 堆的定义如下： n个元素的序列{k1,k2,…,kn}当且仅当满足以下关系时，称之为堆： 用一维数组来存储元素，可以将对应的一维数组看成是一个完全二叉树，则堆的含义证明：完全二叉树中的所有非终端结点的值均不小于（或不大于）其左右孩子结点的值 也就是，若序列{k1,k2,…,kn}是堆，则堆顶元素必为序列中的n个元素的最大（最小）值，如下： {96，83，27，38，11，9} 图上对应的红标代表用于存储的
C++ 堆排序
辛旭东小小工作室
03-13 315
堆排序的原理： 堆是一棵完全二叉树，堆满足两个属性： （1）堆的每一个父节点的值都大于（或小于）其子节点； （2）树是完全平衡的，最底层的叶节点都位于最左边的位置上。 大顶堆： （1）首先，通过“左右节点”与“父节点”不断地进行比较，得出最大值作为根节点，这样就形成了一个大顶堆。 （2）然后把最大值拿出来，放到后面的位置，这样元素就减少一个，之后再去重新建堆。 （3）不断的重复...
c++ 堆排序
weixin_39849839的博客
10-26 167
topk 最小 class Solution { public: void sift_up(vector<int> vec, int size){ int cur=size; int p,tmp; while(cur>=1){ p=cur>>1; if(vec[cur]>vec[p]){ tmp=vec[p];
C++堆排序算法详解与实践.zip
资源摘要信息:"C++堆排序C++堆排序.zip" 堆排序是计算机科学中的一种排序算法，它是基于比较的排序算法，通过构建二叉堆数据结构来实现。堆是一种特殊的完全二叉树，所以它满足完全二叉树的性质：每一层的节点都是...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值