Problem Description
Input
The first line of input gives the number of cases, T. T test cases follow, each on a separate line. Each test case contains one positive integer n. (1 <= n <= 10^9)
Output
For each input case, you should output the answer in one line.
Sample Input
3
1
2
5
Sample Output
9
97
841
Source
HDOJ 2008 Summer Exercise(4)- Buffet Dinner
Recommend
lcy
计算
⌊(2√+3√)2n⌋mod1024
思路:
∵f(n)=(2√+3√)2n=(5+2∗6√)n=An+Bn6√
∴f(n−1)=An−1+Bn−16√
又 ∵f(n)=(5+26√)f(n−1)
∴f(n)=(5An−1+12Bn−1)+(2An−1+5Bn−1)6√
所以递推矩阵就是:
A1=5,B1=2.
然后套矩阵快速幂模板即可求出An,Bn.
又 ∵(5+26√))n=An+Bn6√
∴(5−26√))n=An−Bn6√
∴(5+26√))n+(5−26√)n=2An
又 ∵(5−26√))n<1
∴⌊(5+26√))n⌋=2An−1
所以最后答案就是 2An−1
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<queue>
#include<vector>
#include<map>
#include<stack>
#include<set>
using namespace std;
#define pi acos(-1.0)
#define EPS 1e-6 //log(x)
#define e exp(1.0); //2.718281828
//#define mod 1000000007
#define INF 0x7fffffff
#define inf 0x3f3f3f3f
#pragma comment(linker,"/STACK:102400000,102400000")
typedef long long LL;
#define debug(x) cout<<x<<endl;
#define debug2(x) cout<<x<<" ";
//#define MOD 10000007
LL MOD;
struct Mat{
int n,m;
LL mat[9][9];
};
Mat operator *(Mat a,Mat b){
Mat c;
memset(c.mat,0,sizeof(c.mat));
c.n = a.n,c.m = b.m;
for(int i=1;i<=a.n;i++){
for(int j=1;j<=b.m;j++){
for(int k=1;k<=a.m;k++){
c.mat[i][j] += (a.mat[i][k]*b.mat[k][j])%MOD;
c.mat[i][j] %= MOD;
}
}
}
return c;
}
Mat operator +(Mat a,Mat b){
Mat c;
memset(c.mat,0,sizeof(c.mat));
c.n = a.n,c.m = a.m;
for(int i=1;i<=a.n;i++){
for(int j=1;j<=a.m;j++){
c.mat[i][j] = (a.mat[i][j]+b.mat[i][j])%MOD;
}
}
return c;
}
Mat operator ^(Mat a,LL k){
Mat c;
memset(c.mat,0,sizeof(c.mat));
c.n = a.n,c.m = a.n;
for(int i=1;i<=a.n;i++)c.mat[i][i] = 1;
while(k){
if(k&1){
c = c*a;
}
a = a*a;
k>>=1;
}
return c;
}
void out(Mat a){
for(int i=1;i<=a.n;i++){
for(int j=1;j<=a.m;j++){
printf(j==a.m? "%I64d\n":"%I64d ",a.mat[i][j]);
}
}
}
LL quickPow(LL x, LL n, LL mm)
{
LL a = 1;
while (n)
{
a *= n&1 ? x : 1;
a %= mm;
n >>= 1 ;
x *= x;
x %= mm;
}
return a;
}
int main()
{
int T_T;
scanf("%d",&T_T);
MOD=1024;
Mat pp;
pp.n=pp.m=2;
pp.mat[1][1]=5;
pp.mat[1][2]=12;
pp.mat[2][1]=2;
pp.mat[2][2]=5;
while(T_T--){
scanf("%d",&n);
Mat ans=pp^(n-1);
LL out=(ans.mat[1][1]*5+ans.mat[1][2]*2)%MOD;
printf("%I64d\n",(2*out-1+MOD)%MOD);
}
return 0;
}
/*
_ooOoo_
o8888888o
88" . "88
(| -_- |)
O\ = /O
____/`---'\____
.' \\| |// `.
/ \\||| : |||// \
/ _||||| -:- |||||- \
| | \\\ - /// | |
| \_| ''\---/'' | |
\ .-\__ `-` ___/-. /
___`. .' /--.--\ `. . __
."" '< `.___\_<|>_/___.' >'"".
| | : `- \`.;`\ _ /`;.`/ - ` : | |
\ \ `-. \_ __\ /__ _/ .-` / /
======`-.____`-.___\_____/___.-`____.-'======
`=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
I have a dream!A AC deram!!
orz orz orz orz orz orz orz orz orz orz orz
orz orz orz orz orz orz orz orz orz orz orz
orz orz orz orz orz orz orz orz orz orz orz
*/








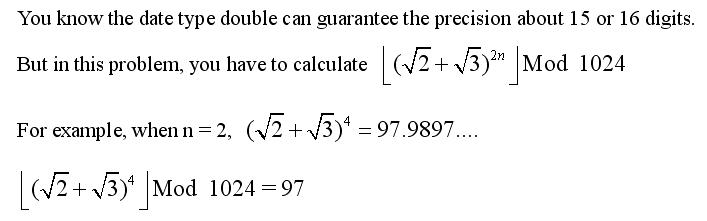
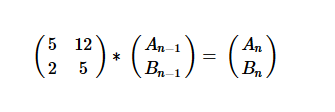














 970
970

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








