1.简单理论介绍
1.1 k-近邻算法的工作原理
k-近邻算法(KNN)的工作原理是:我们有一个样本集,里面的每个数据都存在标签,即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后,依据数据的特征来计算新数据和样本集中数据的距离(这儿采用欧式距离),将计算后的距离按升序排序,选取距离最近的前k(一般小于20)个样本数据,将新数据的类别划分到这k个样本数据中所属类别最多的类。
1.2 欧氏距离
1.3 k-近邻算法优缺点
优点:精度高、对异常值不敏感、无数据输入假定
缺点:计算复杂度高、空间复杂度高、无法给出数据的基础结构信息
适用数据范围:数值型和标称型
2.伪代码
对未知类别属性的数据集中的每个点依次执行以下操作:
1)计算已知类别数据集中的点与当前点之间的距离;
2)按照距离递增次序排序;
3)选取与当前点距离最小的k个点;
4)确定前k个点所在类别的出现频率;
5)返回前k个点出现频率最高的类别作为当前点的预测分类。
3.算法实现
import numpy as np
import operator
# k-NearestNeighbor分类器
# inX:用于分类的输入向量(1xN),dataSet:输入的训练样本(MxN),labels:标签向量(1xM),k:确定最后选择的最邻近邻居的数目。其中,M为样本数目,N为特征个数
def classify(inX,dataSet,labels,k):
#计算欧式距离
m = dataSet.shape[0]#得到输入训练样本的行数,即M
diffMat = np.tile(inX,(m,1)) - dataSet#以inX为模板,复制M行,构成一个新的矩阵,然后减去训练样本矩阵
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)# 1xM
distances = sqDistances**0.5
#选择距离最小的k个点
sortedDistIndicies = distances.argsort()# 将距离进行排序,然后把排序后的距离原来位置的索引存入。
classCount={}# dict
for i in range(k):
voteIlabel =labels[sortedDistIndicies[i]] # 得到所属标签
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1# 将所属标签存入classCount字典中,以voteIlabel为健,以频数为值
sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1), reverse=True)# 将classCount转为iterable,指定以它的第二个域(即值)降序排序
return sortedClassCount[0][0]4. 测试算法
# 创建训练样本
def createDataSet():
group = np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels = ['A','A','B','B']
return group, labels
group,labels = createDataSet()
print 'group:',group
print 'labels:',labels
data = [0,0]# 新数据
data_label = classify(data,group,labels,3)
print 'data_label:',data_label运行结果:
group: [[ 1. 1.1]
[ 1. 1. ]
[ 0. 0. ]
[ 0. 0.1]]
labels: ['A', 'A', 'B', 'B']
data_label: B
5.示例:改进约会网站的配对效果
有1000行如下格式的数据:
40920 8.326976 0.953952 3
14488 7.153469 1.673904 2
26052 1.441871 0.805124 1
75136 13.147394 0.428964 1
38344 1.669788 0.134296 1
72993 10.141740 1.032955 1前三列数据为特征,最后一列数据为类别。详细的来说,第一列数据表示每年获得的飞行常客里程数,第二列数据表示玩视频游戏所耗时间百分比,第三列数据表示每周消费的冰激凌公升数,现在要做的是根据这三个特征,来判断这个人所属类别。
5.1 将文本内容转为矩阵/向量
由于使用向量计算会提升速度,所以需要将文本内容转为向量格式。
代码实现:
#text-->matrix
#将文本转为特征矩阵和标签向量
#filename:数据文件路径
def file2matrix(filename):
fr = open(filename)
arrayOLines = fr.readlines()#一次读取所有内容,并按行将内容存入list
numberOfLines = len(arrayOLines)#文件行数,这儿即训练样本个数M
returnMat = np.zeros((numberOfLines,3))#创建一个M行,3列的矩阵
classLabelVector = []
index = 0
for line in arrayOLines:
line = line.strip()
listFromLine = line.split('\t')
returnMat[index,:] = listFromLine[0:3]# 将前3个元素存入到特征矩阵中
classLabelVector.append(np.int(listFromLine[-1]))
index += 1
return returnMat,classLabelVector
path = r'D:\machine learning\machine learning in action\ch02\data\datingTestSet2.txt'
datingDataMat,datingLabels = file2matrix(path)
print 'data:',datingDataMat
print 'label:',datingLabels[:20]运行结果:
data: [[ 4.09200000e+04 8.32697600e+00 9.53952000e-01]
[ 1.44880000e+04 7.15346900e+00 1.67390400e+00]
[ 2.60520000e+04 1.44187100e+00 8.05124000e-01]
...,
[ 2.65750000e+04 1.06501020e+01 8.66627000e-01]
[ 4.81110000e+04 9.13452800e+00 7.28045000e-01]
[ 4.37570000e+04 7.88260100e+00 1.33244600e+00]]
label: [3, 2, 1, 1, 1, 1, 3, 3, 1, 3, 1, 1, 2, 1, 1, 1, 1, 1, 2, 3]5.2 归一化数据
由于第一个特征的的数值比第二个和第三个特征的数值大很多,为了避免这种情况对最后距离计算的影响,需要对数据进行归一化处理,即将所有数据归一化到0到1之间。归一化可以使用下面的公式:
代码实现:
# normalization
# formula:newValue = (oldValue-min)/(max-min)
# dataSet:给定的数据集
def autoNorm(dataSet):
minVals = dataSet.min(axis=0)#取得每个每一列的最小值,即每个特征中的最小值(1xN)
maxVals = dataSet.max(axis=0)#取得每个每一列的最大值,即每个特征中的最大值(1xN)
ranges = maxVals - minVals#得到每个特征的range(1xN)
normDataSet = np.zeros(dataSet.shape)
m = dataSet.shape[0]
normDataSet = dataSet - np.tile(minVals,(m,1))# MxN
normDataSet = normDataSet/np.tile(ranges,(m,1))# numpy“/”表示具体特征值相除
return normDataSet,ranges,minVals
norMat,ranges,minVals = autoNorm(datingDataMat)
print 'norMat:',norMat
print 'ranges:',ranges
print 'minVals:',minVals运行结果:
norMat: [[ 0.44832535 0.39805139 0.56233353]
[ 0.15873259 0.34195467 0.98724416]
[ 0.28542943 0.06892523 0.47449629]
...,
[ 0.29115949 0.50910294 0.51079493]
[ 0.52711097 0.43665451 0.4290048 ]
[ 0.47940793 0.3768091 0.78571804]]
ranges: [ 9.12730000e+04 2.09193490e+01 1.69436100e+00]
minVals: [ 0. 0. 0.001156]5.3 测试算法
def datingClassTest():
hoRatio = 0.10 #使用90%的数据去训练,10%的数据去测试
path = r'D:\machine learning\machine learning in action\ch02\data\datingTestSet2.txt'
datingDataMat,datingLabels = file2matrix(path) #load data setfrom file
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
if (classifierResult != datingLabels[i]): errorCount += 1.0
print "the total error rate is: %f" % (errorCount/float(numTestVecs))
print errorCount
datingClassTest()运行结果:
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 2, the real answer is: 3
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 3
the classifier came back with: 3, the real answer is: 3
...
the classifier came back with: 2, the real answer is: 2
the classifier came back with: 1, the real answer is: 1
the classifier came back with: 3, the real answer is: 1
the total error rate is: 0.050000
5.0下一篇:决策树





 本文详细介绍了K-近邻算法的工作原理,包括欧氏距离的计算,以及算法的优缺点。通过伪代码展示了算法的执行过程,并提供了一个实际案例——用K-近邻算法改进约会网站的配对效果,包括数据预处理的文本转向量和归一化步骤,最后验证了算法的实施结果。
本文详细介绍了K-近邻算法的工作原理,包括欧氏距离的计算,以及算法的优缺点。通过伪代码展示了算法的执行过程,并提供了一个实际案例——用K-近邻算法改进约会网站的配对效果,包括数据预处理的文本转向量和归一化步骤,最后验证了算法的实施结果。
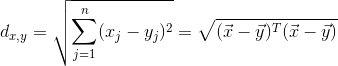
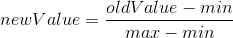
















 448
448

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








