[BZOJ 1013] JSOI 2008 球形空间产生器sphere · 高斯消元

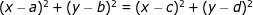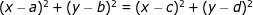预处理以后就是高斯消元模板了，而且还只有唯一解。。。n=2时，设球心是(x,y),则对于任意两个球面上的点(a,b) (c,d)，有，化简以后把每两个相邻的点做成一条方程，n+1个点就构成了n个方程。
然后就高斯消元搞起。

然后就没了。

#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <iostream>
#include <cmath>
using namespace std;
#define zero 1e-6
 
int n;
double ans[15],a[15][15],d[15][15];
//a为方程组矩阵 d为读入数据 
 
void init(){
    cin>>n;
    for (int i=1;i<=n+1;i++)
        for (int j=1;j<=n;j++) cin>>d[i][j];
    for (int i=1;i<=n;i++){
        for (int j=1;j<=n;j++) 
            a[i][j] = 2 * (d[i+1][j]-d[i][j]),
            a[i][n+1] += d[i+1][j] * d[i+1][j] - d[i][j] * d[i][j];
    }
    memset(ans,0,sizeof ans);
}
 
void gauss(){
    for (int i=1;i<n;i++){
        if (fabs(a[i][i])<zero)      //要保证当前 处理的这项系数不为0 
            for (int j=i+1;j<=n;j++)
                if (abs(a[j][i])>zero){
                    for (int k=1;k<=n+1;k++) swap(a[i][k],a[j][k]);
                    break;
                } 
        for (int j=i+1;j<=n;j++){
            double x = a[j][i] / a[i][i];
            for (int k=i;k<=n+1;k++) a[j][k] -= a[i][k] * x;
        }
    }
    ans[n]=a[n][n+1]/a[n][n];
    for (int i=n-1;i;i--){
        for (int j=i+1;j<=n;j++) a[i][n+1] -= ans[j]*a[i][j];
        ans[i] = a[i][n+1] / a[i][i];
    }
}
 
void print(){
    for (int i=1;i<n;i++) printf("%.3lf ",ans[i]);
    printf("%.3lf\n",ans[n]);
}
 
int main(){
    init();
    gauss();
    print();
    return 0;
}