C++ 最小生成树之Prim（普里姆）算法

最小生成树之Prim（普里姆）算法

最小生成树：是在一个给定的无向图G(V,E)中求一棵树T，使得这棵树拥有图G中的所有顶点，且所有边都是来自图G中的边，并且满足整棵树的边权之和最小。

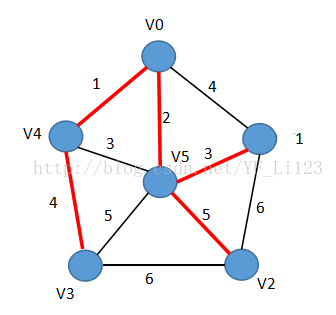
如上图给出了一个图G及其最小生成树T，其中红色的线即为最小生成树的边。最小生成树T包含了图G中所有的顶点，且由它们生成的树的边权之和为15，是所有生成树中权值最小的。

最小生成树有3个性质：

（1）最小生成树是树，因此其边数等于定点数减1，且树内一定不会有环；

（2）对给定的图G(V,E)，其最小生成树可以不唯一，但是其边权之和一定是唯一的；

（3）由于最小生成树是无向图上生成的，因此其根结点可以是这棵树上的任意一个结点。

Prim算法

Prim算法是用来解决最小生成树问题的。

基本思想：对图G（V,E）设置集合S，存放已经被访问的顶点，然后每次从集合V-S中选择与集合S的最短距离最小的一个顶点（记为u），访问并加入集合S。之后，令顶点u为中介点，优化所有从u能到达的顶点v与集合S之间的最短距离。这样的操作执行n次（n为顶点个数），直到集合S已包含所有顶点。

注意：可以发现，prim算法的思想和最短路径中Dijkstra算法的思想几乎完全相同，只是在涉及最短距离时使用了集合S代替Dijkstra算法中的起点s。

下面举例来说明一下prim是如何求最小生成树的。

假设从顶点V0开始， 当前集合V={V0,V1,V2,V3,V4,V5}（蓝色），集合S={}（黄色），顶点V0与集合S之间的距离为0，其它均为INF（一个很大的数） ：

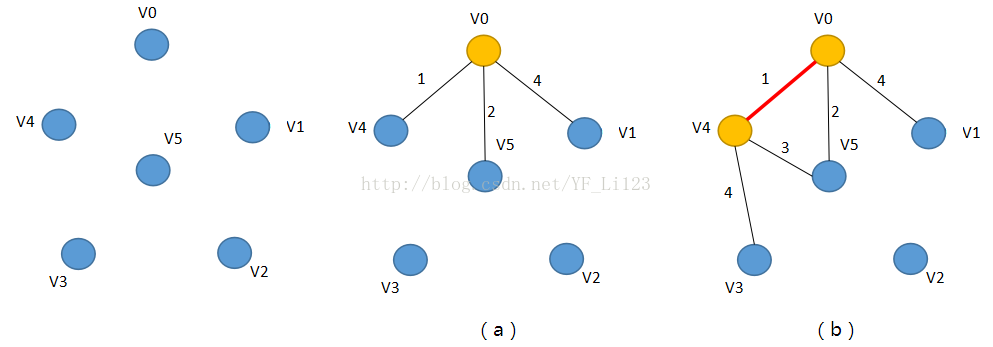
（1）如图(a)，选择与集合S距离最小的顶点V0，将其加入到集合S中，并连接顶点V0与其它顶点的边，此时 集合V={V1,V2,V3,V4,V5}，集合S={V0}；

（2）如图(b)，选择与集合S距离最小的顶点V4， 将其加入到集合S中，并连接顶点V4与其它顶点的边，此时 集合V={V1,V2,V3,V5}，集合S={V0,V4}；

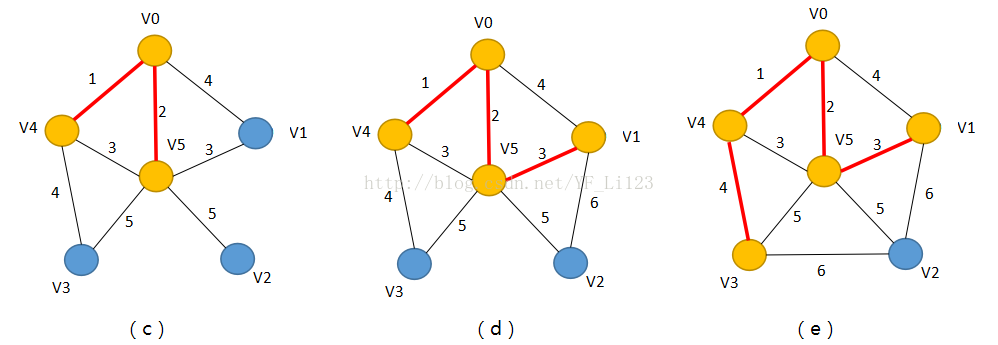
（3）如图(c)，选择与集合S距离最小的顶点V5， 将其加入到集合S中，并连接顶点V5与其它顶点的边，此时 集合V={V1,V2,V3}，集合S={V0,V4,V5}；

（4）如图(d)，选择与集合S距离最小的顶点V1， 将其加入到集合S中，并连接顶点V1与其它顶点的边，此时 集合V={V2,V3}，集合S={V0,V1,V4.V5}；

（5）如图(e)，选择与集合S距离最小的顶点V3， 将其加入到集合S中，并连接顶点V3与其它顶点的边，此时 集合V={V2}，集合S={V0,V1,V3,V4,V5}；

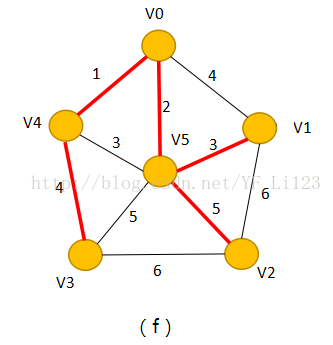
（6）如图(f)，最后选择顶点V2， 将其加入到集合S中，此时 集合V={}，集合S={V0,V1,V2,V3,V4,V5}；

此时集合S已经包含了所有的顶点，算法结束。

Prim算法流程：

对图G（V,E）设置集合S，存放已经被访问的顶点，然后执行n次下面的两个步骤（n为顶点个数）：

1. 每次从集合V-S中选择与集合S的最短距离最小的一个顶点（记为u），访问并加入集合S，同时把这条离集合最近的边加入到最小生成树中。
2. 令顶点u为中介点，优化所有从u能到达的未访问的顶点v与集合S之间的最短距离。

具体实现：

prim算法需要实现两个关键的概念，即集合S的实现，顶点Vi(0<=i<=n-1)与集合S的最短距离。

• 集合S的实现使用一个bool型数组vis[]表示顶点是否已经被访问，其中vis[i]=true表示顶点Vi已被访问，vis[i]=false则表示顶点Vi未被访问；
• 令int型数组d[]来存放顶点Vi与集合S的最短距离。初始时除了起点s的d[s]=0，其余顶点赋值为一个很大的数来表示INF，即不可达。

伪代码如下：

//G为图，数组d为顶点与集合S的最短距离
Prim(G, d[]){
     初始化;
     for(循环n次){
          u = 使d[u]最小的未被访问的顶点的标号;
          记u已被访问;
          for(从u出发能到达的所有顶点v){
               if(v未被访问 && 以u为中介点使得v与集合S的最短距离d[v]更优){
                    将G[u][v]赋值给v与集合S的最短距离d[v]; 
               } 
          } 
     }
}

具体代码实现：

邻接矩阵版：

const int INF = 1000000000;

/*Prim算法求无向图的最小生成树，返回最小生成树的边权之和*/
int Prim(int n, int s, vector<vector<int>> G, vector<bool>& vis, vector<int>& d)
{
       /*
       param
       n:                                     顶点个数
       s:                                     初始点
       G:                                     图的邻接矩阵
       vis:                                   标记顶点是否已被访问
       d:                                     存储顶点与集合S的最短距离
       return:                                最小生成树的边权之和
       */
       fill(d.begin(), d.end(), INF);                                        //初始化最短距离，全部为INF
       d[s] = 0;                                                             //初始点与集合S的距离为0
       int sum = 0;                                                          //记录最小生成树的边权之和
       for (int i = 0; i < n; ++i)
       {
              int u = -1;                                                    //u使得d[u]最小
              int MIN = INF;                                                 //记录最小的d[u]
              for (int j = 0; j < n; ++j)                                    //开始寻找最小的d[u]
              {
                     if (vis[j] == false && d[j] < MIN)
                     {
                           MIN = d[j];
                           u = j;
                     }
              }
              //找不到小于INF的d[u]，则剩下的顶点与集合S不连通
              if (u == -1)
                     return -1;
              vis[u] = true;                                                  //标记u为已访问
              sum += d[u];                                                    //将与集合S距离最小的边加入到最小生成树
              for (int v = 0; v < n; ++v)
              {
                     //v未访问 && u能够到达v && 以u为中介点可以使v离集合S更近
                     if (vis[v] == false && G[u][v] != INF && G[u][v] < d[v])
                           d[v] = G[u][v];                                    //更新d[v]
              }
       }
       return sum;                                                            //返回最小生成树的边权之和
}

邻接表版

const int INF = 1000000000;
struct Node
{
       int v;
       int dis;
       Node(int x, int y):v(x),dis(y){}
};

int Prim(int n, int s, vector<vector<Node>> Adj, vector<bool>& vis, vector<int>& d)
{
       /*
       param
       n：                       顶点个数
       s：                       初始点
       Adj：                     图的邻接表
       vis：                     标记顶点是否被访问
       d：                       存储起点s到其他顶点的最短距离
       return:                   最小生成树的边权之和
       */
       fill(d.begin(), d.end(), INF);                                //初始化最短距离，全部为INF
       d[s] = 0;                                                     //初始点与集合S的距离为0
       int sum = 0;                                                  //记录最小生成树的边权之和
       for (int i = 0; i < n; ++i)
       {
              int u = -1;                                            //u使得d[u]最小
              int MIN = INF;                                         //记录最小的d[u]
              for (int j = 0; j < n; ++j)                            //开始寻找最小的d[u]
              {
                     if (vis[j] == false && d[j] < MIN)
                     {
                           MIN = d[j];
                           u = j;
                     }
              }
              //找不到小于INF的d[u]，则剩下的顶点与集合S不连通
              if (u == -1)
                     return -1;
              vis[u] = true;                                          //标记u为已访问
              sum += d[u];                                            //将与集合S距离最小的边加入到最小生成树
              for (int j = 0; j < Adj[u].size(); ++j)
              {
                     int v = Adj[u][j].v;
                     if (vis[v] == false && Adj[u][j].dis < d[v])
                           d[v] = Adj[u][j].dis;                      //更新d[v]
              }
       }
       return sum;
}

测验上面的例子代码如下：

int main()
{
	int n = 6;
	/*邻接矩阵*/
	//vector<vector<int>> G = { {0,4,INF,INF,1,2},
	//											{4,0,6,INF,INF,3},
	//											{INF,6,0,6,INF,5},
	//											{INF,INF,6,0,4,5},
	//											{1,INF,INF,4,0,3},
	//											{2,3,5,5,3,0} };

	/*邻接表*/
	vector<vector<Node>> Adj = { {Node(4,1),Node(5,2),Node(1,4)},
	{Node(0,4),Node(5,3),Node(2,6)},
	{Node(1,6),Node(3,6),Node(5,5)},
	{Node(2,6),Node(4,4),Node(5,5)},
	{Node(0,1),Node(5,3),Node(3,4)},
	{Node(0,2),Node(1,3),Node(2,5),Node(3,5),Node(4,3)} };
	/*for (auto x : Adj)
	{
		for (auto y : x)
			cout << y.v<<"-"<<y.dis << "  ";
		cout << endl;
	}*/
	vector<bool> vis(n);
	vector<int> d(n);
//	int res = Prim(n, 0, G, vis, d);				//邻接矩阵版
	int res = Prim1(n, 0, Adj, vis, d);		//邻接表版
	cout << res << endl;

	return 0;
}

运行结果如下：

时间复杂度为O(n^2)，只与图中顶点个数有关，与边数无关，因此prim算法适用于稠密图。