拉普拉斯矩阵/映射/聚类

　　拉普拉斯矩阵是个非常巧妙的东西，它是描述图的一种矩阵，在降维，分类，聚类等机器学习的领域有很广泛的应用。

什么是拉普拉斯矩阵

拉普拉斯矩阵

　　先说一下什么是拉普拉斯矩阵，英文名为Laplacian matrix，其具体形式得先从图说起，假设有个无向图如下所示，
　　

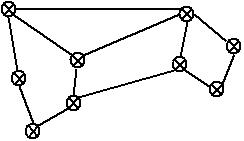
　　其各个点之间的都有相应的边连接，我们用某个指标（这地方可以任意选择，比如欧氏距离、测地距离、或者高斯相似度等）来衡量两个点的相似度，表示为 $W=\sum w_{ij}$，没有边连接的其相似度自然为零， $W$是个对称矩阵；某个点的与所有点的相似度之和，表示为 $D=dig(d); d = rowSum(W)$； $D$是个对角阵；我们的拉普拉斯矩阵则是 $L=D-W$

拉普拉斯矩阵的性质

　　性质：
　　（1）$L$是半正定矩阵。
　　（2）$L$的最小特值为0，对应特向为全1列向量。
　　（3）对$Lf=\lambda Df$有$m$个非负实特征值，$0=\lambda_1 \leq \lambda_2 \leq ... \leq \lambda_m$.
　　（4）对于任意一个属于实向量$f \in R^m$，都有此公式成立：
　　$f^TLf = \frac{1}{2}\sum_{i,j=1}^m w_{ij}(f_i-f_j)^2$
　　它又有什么用处呢？跟目标是有关系的，哈哈~
　　证明如下：　　$f$为$m*1$的实数列向量
　　$f^TLf=f^TDf-f^TWf$
　　$=f^T*dig(d)*f-f^TWf$
　　 =∑mi=1dif2i−∑mj=1[∑i=1fj∗wij]fj