题目大意
现在有
N
个正整数
N<=105
Ai<=106
解题思路
这道题我们可以用贪心的思想去完成。因为题目要求代价最小,那么对于我们每一个位置i,在花费相同的时候,我们肯定让 Ai 的值越大越好(结论一)。那我们就根据这个思想对于整个序列进行操作。
假设我们已经对于前k个数计算出了最优解,把序列变成了若干个 A 值相等的块。那么我们可以讨论一下第k + 1个数的情况。
1. Ak+1<= 最后一个块的高度
因为前面的操作对这个数没有影响,所以代价不变。
2.
Ak+1>
最后一个块的高度
对于这种情况分析比较复杂,我们先分两种情况讨论。
1. 对于只有两个数时,我们肯定是将第一个数增加,因为对于两个数我把第一个数增加和把第二个数减小的代价是一样的,对于相对高度的影响也是一样,那么根据结论一,我们是将第一个数增加。(情况一)
2. 那么假如前面有两个没有改变过的相同的数,现在加入一个比他们都大的数,那么应该怎么变化?因为我们现在只考虑前k + 1个数的情况,我们首先要求权值最小,那么肯定是让第三个数减少到与前两个数的相等。因为我这里少减少1,那么前面就要多增加2,需要的权值就增加了。所以不满足只有两个数的性质。(情况二)
现在我们对推广到一般情况:我们考虑将新加入的一个数合并到最后一个块。对于值相等的一块,其中的某些数可能改变过,我们设修改后的数为
Bi
。那么就要考虑所有
Ai
和
Bi
的关系。我们设
Ai<=Bi
个数为x,
Ai>Bi
个数为y。(这一组数的所有
Bi
相等,下面称这组的
Bi
值为
B
)
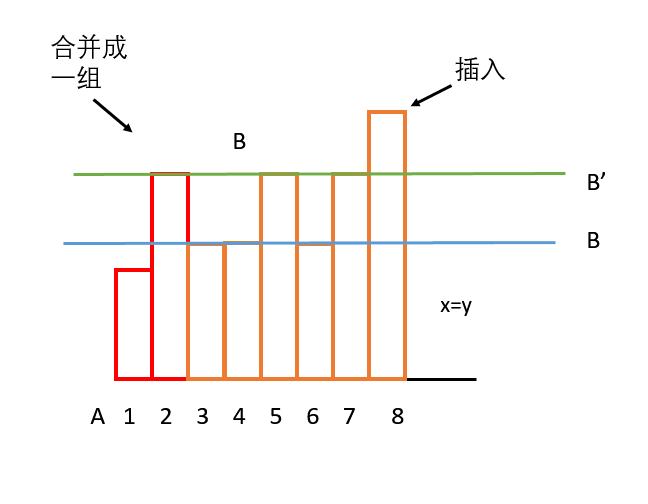
1. x = y:那么我们可以把他们两两分组,那么就跟情况一类似。但是我们新的B 最大只能增加到这组中大于原来的
B
的最小Ai (这个可以用主席树维护),当然如果上一组的
B
值小于最小的Ai 那么就要将上这一组与上一组合并(把高度增加到上一组的
B
值),因为再增加的话就会破坏x = y的前提。这种情况代价不变,只是把当前最后一个数的高度尽量抬高。
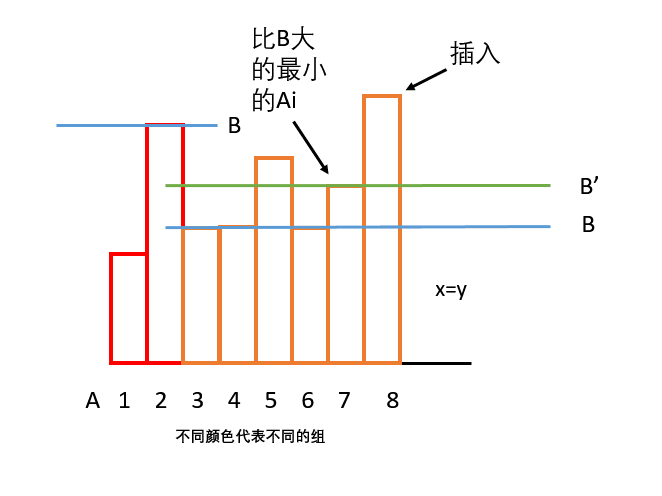
2. x > y:这种情况就跟上面提到的情况二类似,由于这些数不能两两匹配,而当前的首要条件是权值最小,所以我们不能改变B 的值,只能我把
Ak+1
改成
B
,并且增加代价。
3. x < y:不存在,因为在x = y是我们就增加了这组数现在的值进行了操作,至少我一个原来Ai>Bi 的
Ai
改成了
B
<script type="math/tex" id="MathJax-Element-31">B</script>,也就是说减少了y、增加了x。而对于这组的第一个数有是肯定属于x,所以这种情况不存在。
程序
//YxuanwKeith
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + 5, MAXM = 1e6 + 5;
struct Node{
int High, Num, Ok, Left;
Node(int high, int num, int ok, int left) {High = high, Num = num, Ok = ok, Left = left;}
Node(void) {}
};
struct Tree{
int l, r, Num;
} Tr[MAXM * 20];
Node D[MAXN];
int N, top, tot, Max, A[MAXN], Root[MAXN];
void Add(int &Rt, int Lst, int l, int r, int Num) {
Rt = ++ tot;
Tr[Rt] = Tr[Lst];
if (l == r) {
Tr[Rt].Num ++;
return;
}
int Mid = (l + r) >> 1;
if (Num <= Mid) Add(Tr[Rt].l, Tr[Lst].l, l, Mid, Num); else
Add(Tr[Rt].r, Tr[Lst].r, Mid + 1, r, Num);
Tr[Rt].Num = Tr[Tr[Rt].l].Num + Tr[Tr[Rt].r].Num;
}
int Query2(int R1, int R2, int l, int r) {
if (l == r) return l;
int Mid = (l + r) >> 1;
if (Tr[Tr[R1].l].Num - Tr[Tr[R2].l].Num > 0) return Query2(Tr[R1].l, Tr[R2].l, l, Mid); else
return Query2(Tr[R1].r, Tr[R2].r, Mid + 1, r);
}
int Query(int R1, int R2, int l, int r, int lx, int rx) {
if (l == lx && r == rx) {
if (Tr[R1].Num - Tr[R2].Num == 0) return 0; else
return Query2(R1, R2, l, r);
}
int Mid = (l + r) >> 1;
if (rx <= Mid) return Query(Tr[R1].l, Tr[R2].l, l, Mid, lx, rx); else
if (lx > Mid) return Query(Tr[R1].r, Tr[R2].r, Mid + 1, r, lx, rx); else {
int Num = Query(Tr[R1].l, Tr[R2].l, l, Mid, lx, Mid);
if (Num) return Num;
return Query(Tr[R1].r, Tr[R2].r, Mid + 1, r, Mid + 1, rx);
}
}
int Get(int R1, int R2, int l, int r, int Side) {
if (l == r) return Tr[R1].Num - Tr[R2].Num;
int Mid = (l + r) >> 1;
if (Side <= Mid) return Get(Tr[R1].l, Tr[R2].l, l, Mid, Side); else
return Get(Tr[R1].r, Tr[R2].r, Mid + 1, r, Side);
}
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; i ++) {
scanf("%d", &A[i]);
Max = max(Max, A[i]);
}
LL Ans = 0;
D[top = 1] = Node(A[1], 1, 0, 1);
for (int i = 2; i <= N; i ++) {
Root[i] = Root[i - 1];
if (A[i] < D[top].High) D[++ top] = Node(A[i], 1, 0, i); else {
if (A[i] == D[top].High) D[top].Num ++; else {
D[top].Ok ++;
D[top].Num ++;
Ans = Ans + A[i] - D[top].High;
Add(Root[i], Root[i - 1], 1, Max, A[i]);
if (D[top].Ok * 2 == D[top].Num) {
int Min = Query(Root[i], Root[D[top].Left - 1], 1, Max, D[top].High + 1, Max);
int Del = Get(Root[i], Root[D[top].Left - 1], 1, Max, Min);
if (top > 1 && D[top - 1].High <= Min) {
D[top - 1].Num += D[top].Num;
D[top - 1].Ok += D[top].Ok;
if (D[top - 1].High == Min) D[top - 1].Ok -= Del;
top --;
} else {
D[top].High = Min;
D[top].Ok -= Del;
}
}
}
}
}
printf("%lld", Ans);
}
1. 对于只有两个数时,我们肯定是将第一个数增加,因为对于两个数我把第一个数增加和把第二个数减小的代价是一样的,对于相对高度的影响也是一样,那么根据结论一,我们是将第一个数增加。(情况一)
2. 那么假如前面有两个没有改变过的相同的数,现在加入一个比他们都大的数,那么应该怎么变化?因为我们现在只考虑前k + 1个数的情况,我们首先要求权值最小,那么肯定是让第三个数减少到与前两个数的相等。因为我这里少减少1,那么前面就要多增加2,需要的权值就增加了。所以不满足只有两个数的性质。(情况二)
1. x = y:那么我们可以把他们两两分组,那么就跟情况一类似。但是我们新的
2. x > y:这种情况就跟上面提到的情况二类似,由于这些数不能两两匹配,而当前的首要条件是权值最小,所以我们不能改变
3. x < y:不存在,因为在x = y是我们就增加了这组数现在的值进行了操作,至少我一个原来


//YxuanwKeith
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 1e5 + 5, MAXM = 1e6 + 5;
struct Node{
int High, Num, Ok, Left;
Node(int high, int num, int ok, int left) {High = high, Num = num, Ok = ok, Left = left;}
Node(void) {}
};
struct Tree{
int l, r, Num;
} Tr[MAXM * 20];
Node D[MAXN];
int N, top, tot, Max, A[MAXN], Root[MAXN];
void Add(int &Rt, int Lst, int l, int r, int Num) {
Rt = ++ tot;
Tr[Rt] = Tr[Lst];
if (l == r) {
Tr[Rt].Num ++;
return;
}
int Mid = (l + r) >> 1;
if (Num <= Mid) Add(Tr[Rt].l, Tr[Lst].l, l, Mid, Num); else
Add(Tr[Rt].r, Tr[Lst].r, Mid + 1, r, Num);
Tr[Rt].Num = Tr[Tr[Rt].l].Num + Tr[Tr[Rt].r].Num;
}
int Query2(int R1, int R2, int l, int r) {
if (l == r) return l;
int Mid = (l + r) >> 1;
if (Tr[Tr[R1].l].Num - Tr[Tr[R2].l].Num > 0) return Query2(Tr[R1].l, Tr[R2].l, l, Mid); else
return Query2(Tr[R1].r, Tr[R2].r, Mid + 1, r);
}
int Query(int R1, int R2, int l, int r, int lx, int rx) {
if (l == lx && r == rx) {
if (Tr[R1].Num - Tr[R2].Num == 0) return 0; else
return Query2(R1, R2, l, r);
}
int Mid = (l + r) >> 1;
if (rx <= Mid) return Query(Tr[R1].l, Tr[R2].l, l, Mid, lx, rx); else
if (lx > Mid) return Query(Tr[R1].r, Tr[R2].r, Mid + 1, r, lx, rx); else {
int Num = Query(Tr[R1].l, Tr[R2].l, l, Mid, lx, Mid);
if (Num) return Num;
return Query(Tr[R1].r, Tr[R2].r, Mid + 1, r, Mid + 1, rx);
}
}
int Get(int R1, int R2, int l, int r, int Side) {
if (l == r) return Tr[R1].Num - Tr[R2].Num;
int Mid = (l + r) >> 1;
if (Side <= Mid) return Get(Tr[R1].l, Tr[R2].l, l, Mid, Side); else
return Get(Tr[R1].r, Tr[R2].r, Mid + 1, r, Side);
}
int main() {
scanf("%d", &N);
for (int i = 1; i <= N; i ++) {
scanf("%d", &A[i]);
Max = max(Max, A[i]);
}
LL Ans = 0;
D[top = 1] = Node(A[1], 1, 0, 1);
for (int i = 2; i <= N; i ++) {
Root[i] = Root[i - 1];
if (A[i] < D[top].High) D[++ top] = Node(A[i], 1, 0, i); else {
if (A[i] == D[top].High) D[top].Num ++; else {
D[top].Ok ++;
D[top].Num ++;
Ans = Ans + A[i] - D[top].High;
Add(Root[i], Root[i - 1], 1, Max, A[i]);
if (D[top].Ok * 2 == D[top].Num) {
int Min = Query(Root[i], Root[D[top].Left - 1], 1, Max, D[top].High + 1, Max);
int Del = Get(Root[i], Root[D[top].Left - 1], 1, Max, Min);
if (top > 1 && D[top - 1].High <= Min) {
D[top - 1].Num += D[top].Num;
D[top - 1].Ok += D[top].Ok;
if (D[top - 1].High == Min) D[top - 1].Ok -= Del;
top --;
} else {
D[top].High = Min;
D[top].Ok -= Del;
}
}
}
}
}
printf("%lld", Ans);
}























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








