Motion Analysis HTR (分等级模型运动分析)

最新推荐文章于 2021-05-21 09:01:28 发布

张赐

最新推荐文章于 2021-05-21 09:01:28 发布

阅读量5.3k

点赞数

分类专栏：计算机动画文章标签： translation header input 数据结构 vector 扩展

本文链接：https://blog.csdn.net/zhangci226/article/details/3403955

版权

计算机动画专栏收录该内容

5 篇文章 1 订阅

订阅专栏

Motion Analysis HTR

2008-11-17

HTR(Hierarchical Translation-Rotation)是一种分级的模型动画技术，它是从一种.htr文件中读取模型动画信息，然后采用分级模型动画的方法来处理复杂的模型动画。使用3DMAX可以导出这种文件，文件一般由Header，Segment names&hierarchy，Base position，Motion sections这几个部分组成，不同的部份分别记录不同的信息，Header中一般记录有文件类型，数据类型，关键帧数，分级的模型数等等，Segment names&hierarchy中记录了每级模型的名字和它的父节点，Base position中记录了本地变换信息(注意：记录的不是坐标，而是坐标变换)，Motion sections中记录了所有节点在每个关键帧的坐标变换。

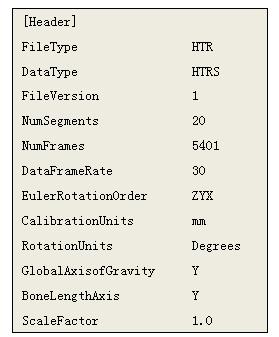
一个htr文件的Header部份

在HTR技术中，我们一般使用的变换都是刚体变换，顾名思义，刚体变换就是指在变换的过程中，模型的形状不发生改变。刚体变换一般指位移变换（Translation），旋转变换（Rotation）和等比的放缩变换（Scaling）。

◆ 旋转变换（Rotation）

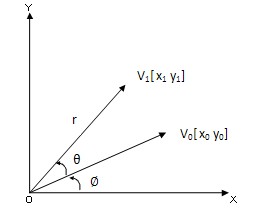
在上面的坐标中，向量V₀逆时针方向旋转到达V₁的位置，现在要用矩阵的乘法来表示这个向量的旋转。假设旋转半径是r，那么旋转后：

$x_{1}=rcos(/theta +/phi )$

$y_{1}=rsin(/theta +/phi )$

上式根据三角公式展开：

$x_{1}=rcos/theta cos/phi -rsin/theta sin/phi$

$x_{1}=rsin/theta cos/phi +rcos/theta sin/phi$

可以得到：

$x_{1}=x_{0}cos/theta -y_{0}sin/theta$

$y_{1}=x_{0}sin/theta -y_{0}cos/theta$

写成矩阵乘法形式，得到：

$/begin{bmatrix} x_{1}// y_{1} /end{bmatrix} = /begin{bmatrix} cos/theta & -sin/theta// sin/theta&cos/theta /end{bmatrix} /begin{bmatrix} x_{0}//y_{0} /end{bmatrix}$

这样就得到了旋转矩阵 $/begin{bmatrix} cos/theta & -sin/theta// sin/theta&cos/theta /end{bmatrix}$ ，实际应用的时候，一般要扩展到三维空间，下面分别是绕X，Y，Z轴旋转的

旋转矩阵：

$/begin{bmatrix} 1&0&0// cos/theta & -sin/theta &0// sin/theta & cos/theta &0 /end{bmatrix}$ $/begin{bmatrix} cos/theta &0& sin/theta // 0&1&0// -sin/theta & 0&/cos/theta /end{bmatrix}$ $/begin{bmatrix} cos/theta &-sin/theta& 0 // sin/theta & cos/theta&0// 0&0&1// /end{bmatrix}$

在计算机处理信息的时候，都采用4X4的矩阵，这就是仿射变换，如下面的形式。

$/begin{bmatrix} 1 &0 &0 &0 // 0&cos/theta &-sin/theta &0 // 0& sin/theta& cos/theta &0 // 0& 0 &0 &1 /end{bmatrix}$ $/begin{bmatrix} cos/theta& 0& sin/theta& 0// 0&1 &0 & 0// -sin/theta&0&cos/theta& 0// 0& 0& 0& 1 /end{bmatrix}$ $/begin{bmatrix} cos/theta& -sin/theta& 0& 0// sin/theta&cos/theta&0& 0// 0&0 &1 & 0// 0& 0& 0& 1 /end{bmatrix}$

◆ 放缩变换（Scaling）

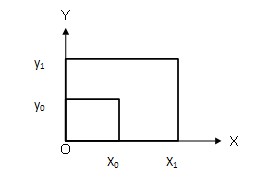
很明显，可以用倍数来描述x₀，x₁，y₀，y₁之间的关系

x₁ = S_x x₀

y₁ = S_y y₀

写成矩阵的形式

$/begin{bmatrix} x_{1}// y_{1} /end{bmatrix} =/begin{bmatrix} S_{x} &0 // 0&S_{y} /end{bmatrix} /begin{bmatrix} x_{0}// y_{0} /end{bmatrix}$

这样就得到了放缩矩阵，同样的也可以扩展到三维空间和它的仿射变换

$/begin{bmatrix} S_{x} &0 &0 // 0& S_{y}&0 // 0&0 & S_{z} /end{bmatrix}$ $/begin{bmatrix} S_{x} &0 &0 &0// 0& S_{y}&0 &0// 0&0 & S_{z}&0// 0&0&0&1 /end{bmatrix}$

◆ 位移变换（Translation）

位移变换是最简单的，但是也比较特殊，因为找不到一个3X3的矩阵来描述一个三维空间的位移变换。所以对于位移，必须使用仿射变换才能把位移描述为矩阵的乘法。也就是说，一个三维空间中的位移，我们用一个4X4的矩阵乘法来描述。也就是前面说的仿射变换。

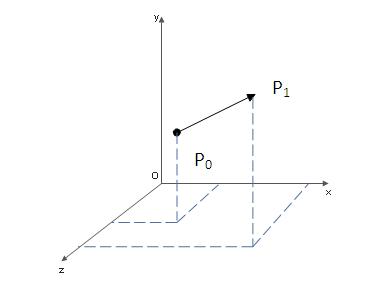
在上面的坐标系中，点P₀分别在X，Y，Z轴方向上移动了 Tx，Ty ， Tz到达点P₁，那么P₁可以表示为：

$/begin{bmatrix} x_{1}// y_{1}// z_{1} /end{bmatrix} = /begin{bmatrix} x_{0}// y_{0}// z_{0} /end{bmatrix} + /begin{bmatrix} T_{x}// T_{y}// T_{z} /end{bmatrix}$

因为不能找到一个3X3的矩阵将位移描述为矩阵的乘法形式，所以要使用仿射变换。它描述为下面的形式：

$/begin{bmatrix} x_{1}// y_{1}// z_{1} /end{bmatrix} = /begin{bmatrix} x_{0}// y_{0}// z_{0} /end{bmatrix} + /begin{bmatrix} T_{x}// T_{y}// T_{z} /end{bmatrix} = /begin{bmatrix} 1 & 0 & 0 & T_{x}// 0& 1 & 0 & T_{y}// 0 & 0& 1& T_{z}// 0&0 &0 & 1 /end{bmatrix} /begin{bmatrix} x_{0}// y_{0}// z_{0}// 1 /end{bmatrix}$

现在为止，所有的变换可以用一个变换矩阵来描述：

$M= /begin{bmatrix} R & T// 0& 1 /end{bmatrix}$

R表示旋转矩阵，T表示位移矩阵。常常我们会用到该变换矩阵的逆矩阵，它表示为：

$M^{-1}= /begin{bmatrix} R^T & -R^TT// 0& 1 /end{bmatrix}$

◆ 四元数（Quaternion）

现在已经有了旋转矩阵了，但是它们都是围绕坐标轴旋转，不能满足实际应用，实际情况中，很多时候我们要用想使一个物体绕任意轴旋转，下面是一个绕任意轴r旋转 $/theta$ 度的矩阵。

$R= /begin{bmatrix} cos/theta+(1-cos/theta)r^{2}_{x} &(1-cos/theta)r_{x}r_{y}-r_{z}sin/theta &(1-cos/theta)r_{x}r_{z}+r_{y}sin/theta // (1-cos/theta)r_{x}r_{y}+r_{z}sin/theta &cos/theta+(1-cos/theta)r^{2}_{y}& (1-cos/theta)r_{y}r_{z}-r_{x}sin/theta // (1-cos/theta)r_{x}r_{z}-r_{y}sin/theta&(1-cos/theta)r_{y}r_{z}+r_{x}sin/theta &cos/theta+(1-cos/theta)r^{2}_{z} /end{bmatrix}$

这个矩阵的计算相当复杂，且在实际的应用中，旋转矩阵一直不停的和其他矩阵或点相乘，不能够保证得到的矩阵永远是正交的，所以我们利用四元数来解决这个问题。一个四元数表示如下：

$q=(w,x,y,z)$

那么 $q = ( cos/theta,sin/theta(x,y,z))$ 就表示一个旋转变换，它表示绕轴xyz旋转2 $/theta$ 角度。现在变换矩阵可以写为

$M= /begin{bmatrix} Q & T// 0& 1 /end{bmatrix}$ $M^{-1}= /begin{bmatrix} Q^{T} & -Q^{T}T// 0& 1 /end{bmatrix}$

◆ Motion Analysis HTR

下面的模型展示了一个简单的动作，一个机械臂的上升并且旋转，如下图

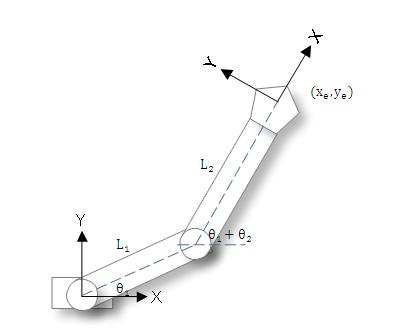
我们可以使用一连串的变换矩阵乘积来描述物体的运动。在该模型中，它的过程是先逆时针旋转 $/theta_{1}$ 角度，然后向X方向移动 $/L_{1}$ 的距离，再逆时针旋转 $/theta_{2}$ 角度，然后再向X方向移动 $/L_{2}$ 的距离。这个变换可以表示为下面的矩阵乘法。

$T=[R(/theta_{1})][T(L_{1})][R(/theta_{2})][T(L_{2})]$

$T= /begin{bmatrix} cos/theta_{1} &-sin/theta_{1} &0 // sin/theta_{1} &cos/theta_{1} &0 // 0& 0&1 /end{bmatrix} /begin{bmatrix} 1 &0 &L_{1} // 0& 1 &0 // 0& 0 &1 /end{bmatrix} /begin{bmatrix} cos/theta_{2} &-sin/theta_{2} &0 // sin/theta_{2} &cos/theta_{2} &0 // 0& 0&1 /end{bmatrix} /begin{bmatrix} 1 &0 &L_{2} // 0& 1 &0 // 0& 0 &1 /end{bmatrix}$

通过上面这个变换矩阵可以得到最后 $(x_{e},y_{e})$ 的世界坐标。

$/begin{bmatrix} x_{e}// y_{e} /end{bmatrix} =/begin{bmatrix} L_{1}cos/theta+L_{2}cos(/theta_{1}+/theta_{2})// L_{1}sin/theta+L_{2}sin(/theta_{1}+/theta_{2}) /end{bmatrix}$

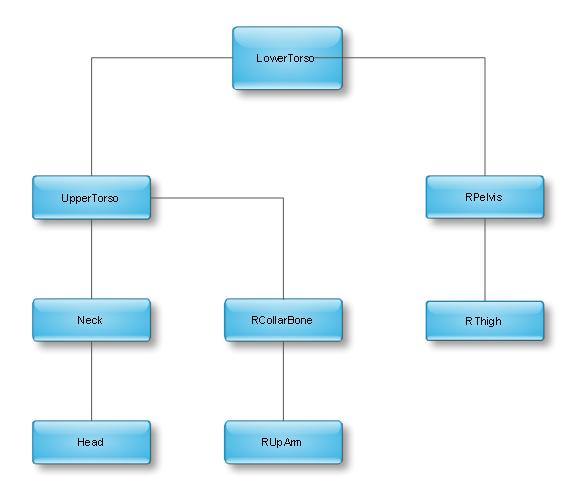
在HTR的方法中，通常要输入模型关键帧的变换，也就是说在这一关键帧中模型保持一个动作，我们要告诉它在下一帧中节点要怎样变换。注意这里指的是变换，而不是节点的坐标，这样做是因为在处理问题时变得简单一些，我们可以不必告诉它所在的世界坐标的位置，这个位置完全可以通过公式来计算，而不是计算后再告诉节点。就好象比如一个人学习跳舞的时候，老师告诉她把手再抬高一点点，这里的“一点点”不是一个坐标，而是“手”相对于它的父节点的变换。所以还要给每个节点指定它的父节点，每个节点都是以它的父节点为基础而变换的。其中有一个节点没有父节点，因为它要作为所有节点的根节点，所有节点都是以根节点为基础的。可以把任意一个节点看成是一个根节点，但是只能有一个根节点。比如一个人的模型动画，我们用LowerTorso作为根节点，像下面这个模型。

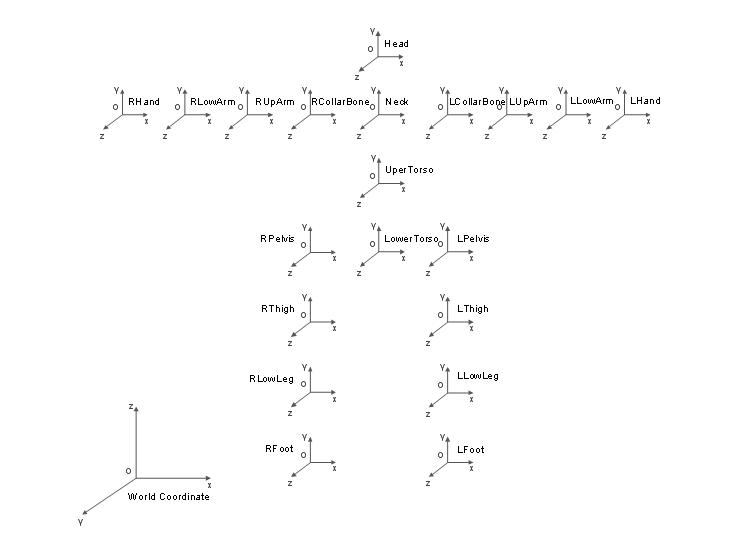
这里使用了20个节点来描述这个模型，每个节点代表人的一个关节，LowerTorso这个节点是所有节点的根节点，初始化的时候，只有它的变换是根据世界坐标变换来计算的，其它子节点都是根据根节点和本地坐标变换来实现的。

下面是htr文件中节点和父节点的信息，左边是节点名，右边是它的父节点。

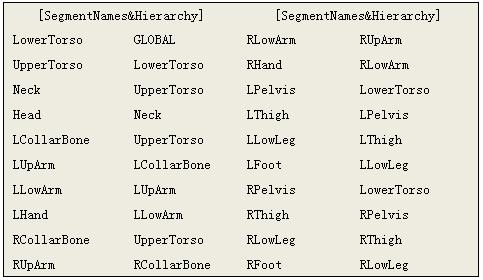
下面通过一个简单的模型来说明如何计算每个节点的本地坐标变换矩阵和世界坐标变换矩阵。

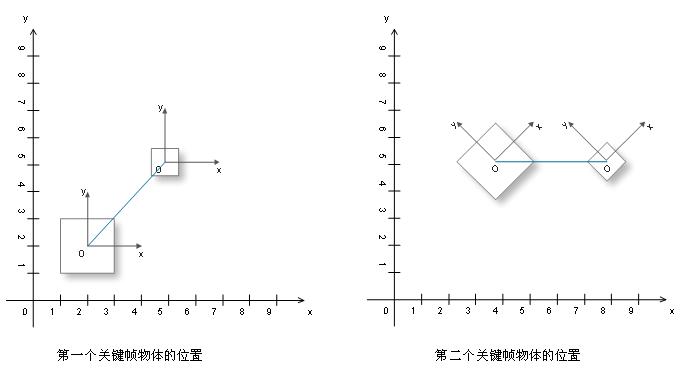
上面是一个由2个正方形组成的物体分别在第一个关键帧和第二个关键帧的位置。我们把大的正方形作为根节点，小正方形作为子节点，小正方形的父节点就是大正方形。所以小正方形一系列的变换都是相对于它的父节点大正方形而变换的。

在第一个关键帧里，我们能看到如上图的这个图形，实际上已经给了物体一些列变换后，物体在世界坐标中才能出如图所示的样子。下面是第一个关键中的变换信息。

这里QuadRoot是根节点，所以它的位置是根据世界坐标变换（Gobal Translation）来计算的。 QuadChild节点的父节点是QuadRoot，所以他的本地坐标变换（Local Translation）就是世界坐标变换。

$GM_{Root}=LM_{Root}= {/color{green} /begin{bmatrix} cos/theta &-sin/theta &0 // sin/theta& cos/theta &0 // 0&0 &1 /end{bmatrix} /begin{bmatrix} 1 & 0 &2 // 0 & 1 &2 // 0& 0 &1 /end{bmatrix} } =/begin{bmatrix} 1 & 0 &2 // 0 & 1 &2 // 0& 0 &1 /end{bmatrix}$

很容易得到了根节点在世界坐标中的位置[2，2]，根节点世界变换和本地变换都是一致的。上式中有绿色的部分就根节点是世界变换矩阵,常常把它写成一个矩阵 $/begin{bmatrix} cos/theta &-sin/theta &2 // sin/theta&cos/theta &2 // 0&0 & 1 /end{bmatrix}$ 这种形式。

有了根节点的世界变换和本地变换矩阵，现在就可以通过QuadRoot来计算QuadChild的变换了。先计算QuadChild的本地变换矩阵。用 $GM_{Child}$ 来表示子节点的世界变换矩阵， $LM_{Child}$ 表示子节点的本地变换矩阵， $LM_{Root}$ 表示父节点的本地变换矩阵，IM表示输入的变换矩阵。

初始化的时候输入的变换矩阵就是节点的本地变换矩阵，所以很容易得到子节点的本地变换矩阵

$LM_{Child}= /begin{bmatrix} 1&0 &3 // 0&1&3// 0&0 & 1 /end{bmatrix}$

接着再来计算它的世界变换矩阵。用下面这个等式。

$GM_{Child}=GM_{Child's Parent} /times LM_{Child}$

所以我们得到：

$GM_{Child}= /begin{bmatrix} 1 &0 &2 // 0&1 &2 // 0&0 &1 /end{bmatrix} /begin{bmatrix} 1 &0 &3 // 0&1 &3 // 0&0 &1 /end{bmatrix} = /begin{bmatrix} 1 &0 &5 // 0&1 &5 // 0&0 &1 /end{bmatrix}$

下面来看看第二个关键帧中的变换。

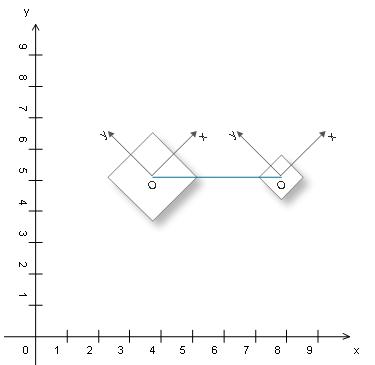
在第二个关键帧中，变换信息如下：

先计算根节点的变换矩阵。

$GM_{Root}=ML_{Root}/times IM= /begin{bmatrix} 1 & 0 &2 // 0& 1 & 2// 0& 0 & 1 /end{bmatrix} /begin{bmatrix} cos45 & -sin45 &2 // sin45& cos45 & 3// 0& 0 & 1 /end{bmatrix} = /begin{bmatrix} cos45 & -sin45 &4 // sin45& cos45 & 5// 0& 0 & 1 /end{bmatrix}$

再通过QuadChild的父节点QuadRoot的本地变换矩阵乘以QuadChild的本地变换矩阵再乘以输入的变换矩阵就可以得世界变换矩阵。

$GM_{Child}=GM_{Child's Parent}/times LM_{Child}/times IM$

计算上面的等式可以得到

$GM_{Child}= /begin{bmatrix} 1 & 0 & 5// 0 & 1 & 5// 0 &0 & 1 /end{bmatrix} /begin{bmatrix} cos45 & -sin45 & 3// sin45 & cos45 & 0// 0 &0 & 1 /end{bmatrix} = /begin{bmatrix} cos45 & -sin45 & 8// sin45 & cos45 & 5// 0 &0 & 1 /end{bmatrix}$

以上的过程就是HTR技术中最核心的部分，通过每个节点的父节点，一直找到根节点，然后一级一级的计算出变换矩阵。这种数据结构可以用树来描述，然后使用深度优先的方法遍历树的节点。下面是个人体模型树形结构的例子。

◆ 实际应用

　　　　在实际的应用中，需要建立两个最主要类，一个是Joint类，它描述了模型的节点。还有一个是Model类，它描述了整个模型。下面的类图详细的描述这两个类。

在Model类中，JointList是用来保存节点信息的vector类型的数组。 GTransf是一个把向量和四元数组成为矩阵的类，frmMotion是自定义的结构体，用来保存htr文件中所有节点数据，它的结构如下。

frame是用来计算帧数， m_NumSegments，m_NumFrames，m_DataFrameRate分别保存了htr文件中[Header]部分的节点数，帧数和帧率。而公有方法FKSolver（）就是用来计算在每个关键帧里，每个节点的世界坐标变换。如果帧率是30，就要在每一秒内调用该方法30次，帧数的计数就用是frame这个参数，如果frame > m_NumFrames，那么frame就重置为0，这样动画就能再次重头开始。下面是设置timer，使FKSolver方法可以在一秒钟内连续调用30次。

下面是FKSolver方法

void Model::FKSolver() { int size = JointList.size(); //获得节点的个数 for (int i = 0; i < size; ++i) //每个节点的循环 { //首先使用GVector3类，GQuater类和GTransf类构造输入变换矩阵，2维数组arrfrmm中已经 //保存了所有输入的数据 GVector3 v(arrfrmm[i][frame].tx, arrfrmm[i][frame].ty, arrfrmm[i][frame].tz); GQuater q(arrfrmm[i][frame].rx, arrfrmm[i][frame].ry, arrfrmm[i][frame].rz, EULER_ZYX); GTransf input(v,q); if( i == 0 ) { //如果是根节点，那么它的世界变换矩阵等于它的本地变换矩阵乘以输入矩阵，就是前面 //等式中的GM_Root=LM_Root×IM JointList[i]->SetX( JointList[i]->GetDelX() * input ); } else { //如果不是根节点，那么 //GM_Child=GM_(Child^' sParent)×LM_Child×IM JointList[i]->SetX( JointList[i]->GetParent()->GetX() * JointList[i]->GetDelX() * input); } glPushMatrix(); GMatrix gmT = form_mat(JointList[i]->GetInX()); double *X = form_arr(gmT); glMultMatrixd( X ); glPopMatrix(); } if( ++frame > 5401 ) //如果帧播放完毕就重新开始 frame = 0; }

对于Joint类，主要是获取和设置每个节点的父节点的信息，并且设置初始状态的世界变换矩阵和本地变换矩阵。下面是主要代码部分。

// // Set up the Name and Parent of the Joint // if( str == "[SegmentNames&Hierarchy]" ) { for(int i =0;i<model.m_NumSegments ;++i) { string str1,str2; in >> str1 >>str2; Joint* joint = new Joint( str1 ); model.JointList.push_back(joint); if( str1 == "LowerTorso" ) { joint->SetParent(0);//如果是根节点，那么设置父节点为空 } else { //做一个循环，JointList中寻找和自己父节点名字相同的节点，并把这个点 //设置为自己的父节点 for( int j = 0; j<i; ++j ) { if( str2 == model.JointList[j]->GetName() ) { joint ->SetParent(model.JointList[j]); } } } } break; }

由于不能发布视频，使用HTR技术完成的骨骼动画请看这里　http://kr.youtube.com/watch?v=uzmQFWkEYFU

*原创文章，转载请注明出处*

int CViewerView::OnCreate(LPCREATESTRUCT lpCreateStruct) { 　　if (GView::OnCreate(lpCreateStruct) == -1) 　　　　return -1; 　　SetTimer(0,1000/30,NULL); //每秒执行30次　　return 0; }

void CViewerView::OnTimer(UINT_PTR nIDEvent) { 　　model.FKSolver(); 　　Invalidate(false); 　　GView::OnTimer(nIDEvent); }

张赐

关注

0
点赞
踩
7

收藏

觉得还不错? 一键收藏
打赏
2
评论
Motion Analysis HTR (分等级模型运动分析)

Motion Analysis HTR 2008-11-17 HTR(Hierarchical Translation-Rotation)是一种分级的模型动画技术，它是从一种.htr文件中读取模型动画信息，然后采用分级模型动画的方法来处理复杂的模型动画。使用3DMA
复制链接

扫一扫