平衡二叉树——AVL树的实现

AVL树是最先发明的自平衡二叉查找算法，是平衡二叉树的一种。在AVL中任何节点的两个儿子子树的高度最大差别为1，所以它又被成为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来平衡这棵树。

假设把AVL树构造过程中需要重新平衡的节点叫做α。由于任意节点最多有两个儿子，因此高度不平衡时，α点的两颗子树的高度差2。这种不平衡可能出现在下面这四种情况：

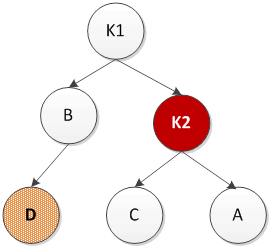
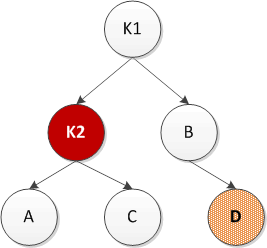
1）  对α的左儿子的左子树进行一次插入（左旋）

其中D是新插入的节点，红色节点K2是失去平衡的节点。需要对K1和K2进行左旋调整即将K1作为根，将K2作为K1的左子树，K1的右子树调整为K2的左子树。如下图所示

进行左旋变换   

代码如下：

static Position SingleRotateWithLeft(Position K2)
{
    Position K1;

    K1 = K2->Left;
    K2->Left = K1->Right;
    K1->Right = K2;
    //更新节点的高度
    return K1;
}

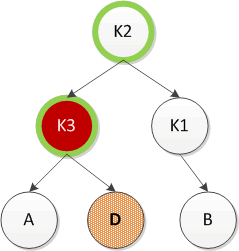
2）对α的左儿子的右子树进行一次插入（左右双旋）

左右双旋这里的左右指的是对α的左儿子的右子树进行插入时需要旋转。先对K1和K2进行右旋（跟第四种情况类似），然后再对K3和K2进行左旋，最终实现平衡。如下图所示

进行一次右旋进行一次左旋

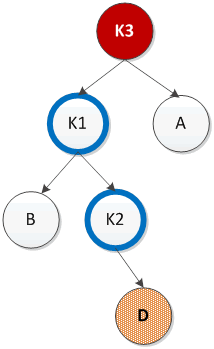
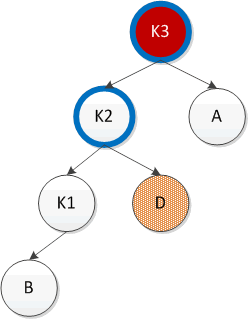
代码如下：

static Position DoubleRotateWithLeft(Position K3)
{
    K3->Left = SingleRotateWithRight(K3->Left);
    return SingleRotateWithLeft(K3);
}

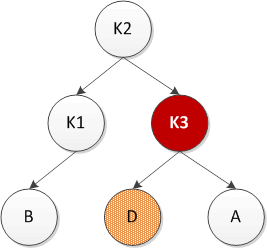
3）对α的右儿子的左子树进行一次插入（右左双旋）

右左双旋：先对K1和K2进行左旋，然后在对K2和K3进行右旋，最终实现平衡。如下图所示

进行一次左旋进行一次右旋

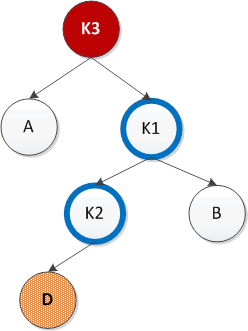
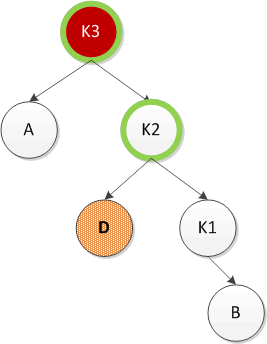
代码如下：

static Position DoubleRotateWithRight(Position K3)
{
    K3->Right = SingleRotateWithLeft(K3->Right);
    return SingleRotateWithRight(K3);
}

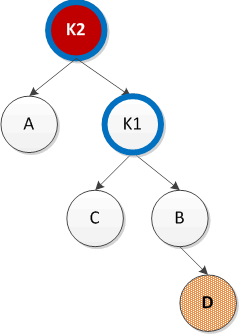
4）对α的右儿子的右子树进行一次插入（右旋）

将K2的右子树更改为K1的左子树，K1的左子树更改为K2即完成的右旋，如下图所示

进行右旋

代码如下：

static Position SingleRotateWithRight(Position K2)
{
	Position K1;

	K1 = K2->Right;
	K2->Right = K1->Left;
	K1->Left = K2;
	//更新节点高度
	return K1;
}

上面讲述了AVL树四种旋转情况，下面来实现一下AVL树。AVL树的实现跟上一章讲的二叉查找树相似，区别在于在插入和删除节点是需要对树进行调整以满足平衡条件。

avltree.h给出函数声明

typedef int ElementType;

#ifndef AVLTREE_H
#define AVLTREE_H

struct TreeNode
{
	ElementType Element;
	int Height;
	struct TreeNode *Left;
	struct TreeNode *Right;
};

typedef struct TreeNode *AvlTree;
typedef struct TreeNode *Position;

AvlTree MakeEmpty(AvlTree T);
AvlTree Insert(ElementType X, AvlTree T);
Position Find(ElementType X ,AvlTree T);
Position FindMax(AvlTree T);
Position FindMin(AvlTree T);

#endif

avltree.c函数实现

#include "fatal.h"
#include "avltree.h"

AvlTree MakeEmpty(AvlTree T)
{
	if(T != NULL)
	{
		MakeEmpty(T->Left);
		MakeEmpty(T->Right);
		free(T);
	}
	return NULL;
}

static int Height(Position P)
{
	if(P == NULL)
		return -1;
	else
		return P->Height;
}

static int Max(int Lhs, int Rhs)
{
	return Lhs > Rhs ? Lhs : Rhs;
}

static Position SingleRotateWithLeft(Position K2)
{
	Position K1;

	K1 = K2->Left;
	K2->Left = K1->Right;
	K1->Right = K2;

	K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1;
	K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;

	return K1;
}

static Position SingleRotateWithRight(Position K2)
{
	Position K1;

	K1 = K2->Right;
	K2->Right = K1->Left;
	K1->Left = K2;

	K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1;
	K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;

	return K1;
}

static Position DoubleRotateWithLeft(Position K3)
{
	K3->Left = SingleRotateWithRight(K3->Left);
	return SingleRotateWithLeft(K3);
}

static Position DoubleRotateWithRight(Position K3)
{
	K3->Right = SingleRotateWithLeft(K3->Right);
	return SingleRotateWithRight(K3);
}

AvlTree Insert(ElementType X, AvlTree T)
{
	if(T == NULL)
	{
		T = (Position)malloc(sizeof(struct TreeNode));
		if(T == NULL)
			FatalError("Out of space");
		T->Element = X;
		T->Height = 0;
		T->Left = T->Right = NULL;
	}
	else if(X < T->Element)//左子树插入新节点
	{
		T->Left = Insert(X, T->Left);
		if(Height(T->Left) - Height(T->Right) == 2)//左子树插入节点所以高度是左子树高于右子树
		{
			if(X < T->Left->Element)//对α的左儿子的左子树进行一次插入，需要左旋
				T = SingleRotateWithLeft(T);
			else //对α的左儿子的右子树进行一次插入，需要双旋
				T = DoubleRotateWithLeft(T);
		}
	}
	else if(X > T->Element)//右子树插入新节点
	{
		T->Right = Insert(X, T->Right);
		if(Height(T->Right) - Height(T->Left) == 2)//因为是右子树插入新节点，所以高度是右子树高于左子树
		{
			if(X > T->Right->Element)//对α的右儿子的右子树进行一次插入，需要右旋
				T = SingleRotateWithRight(T);
			else//对α的右儿子的左子树进行一次插入，需要双旋
				T = DoubleRotateWithRight(T);
		}
	}
	T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
	return T;
}

Position Find(ElementType X, AvlTree T)
{
	if(T == NULL)
		return NULL;
	if(X < T->Element)
		return Find(X, T->Left);
	else if(X > T->Element)
		return Find(X, T->Right);
	else
		return T;
}

Position FindMin(AvlTree T)
{
	if(T == NULL)
		return NULL;
	else if(T->Left == NULL)
		return T;
	else
		return FindMin(T->Left); 
}

Position FindMax(AvlTree T)
{
	if(T == NULL)
		return NULL;
	else if(T->Right == NULL)
		return T;
	else
		return FindMax(T->Right);
}

testavl.c测试AVL树的实现

#include "avltree.h"
#include <stdio.h>
#include <stdlib.h>

void InOrder(AvlTree T)
{
	if(T != NULL)
	{
		InOrder(T->Left);
		printf("%d ", T->Element);
		InOrder(T->Right);
	}
}

void PreOrder(AvlTree T)
{
	if(T != NULL)
	{
		printf("%d ", T->Element);
		PreOrder(T->Left);
		PreOrder(T->Right);
	}
}

int main(void)
{
	AvlTree T;
	Position P;
	int i;

	T = MakeEmpty(NULL);
	for(i = 1; i <= 7; i++)
		T = Insert(i, T);
	for(i = 16; i >= 10; i--)
		T = Insert(i, T);
	T = Insert(8, T);
	T = Insert(9, T);
	printf("Root: %d\n", T->Element);
	printf("InOrder:  ");
	InOrder(T);
	printf("\nPreOrder: ");
	PreOrder(T);
	putchar('\n');
	system("Pause");

	return 0;
}

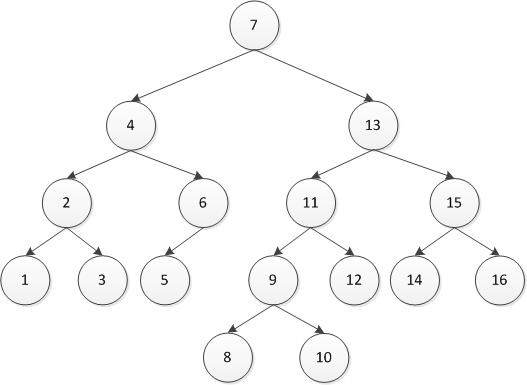
测试：首先插入1到7，然后插入16到10，最后插入8和9。AVL树的应该为下图所示

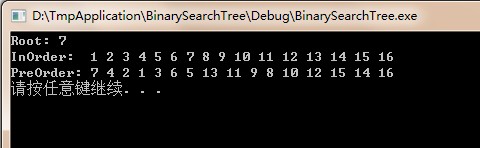
测试结果如下图所示