假期(Holiday)
健佳正在制定下个假期去台湾的游玩计划。在这个假期,健佳将会在城市之间奔波,并且参观这些城市的景点。
在台湾共有 n 个城市,它们全部位于一条高速公路上。这些城市连续地编号为0到n−1 。
对于城市 i(0<i<n−1) 而言,与其相邻的城市是 i−1 和 i+1 。但是对于城市 0 ,唯一与其相邻的是城市1 。而对于城市 n−1 ,唯一与其相邻的是城市 n−2 。
每个城市都有若干景点。健佳有 d 天假期并且打算要参观尽量多的景点。健佳已经选择了假期开始要到访的第一个城市。在假期的每一天,健佳可以选择去一个相邻的城市,或者参观所在城市的所有景点,但是不能同时进行。即使健佳在同一个城市停留多次,他也不会去重复参观该城市的景点。请帮助健佳策划这个假期,以便能让他参观尽可能多的景点。例子
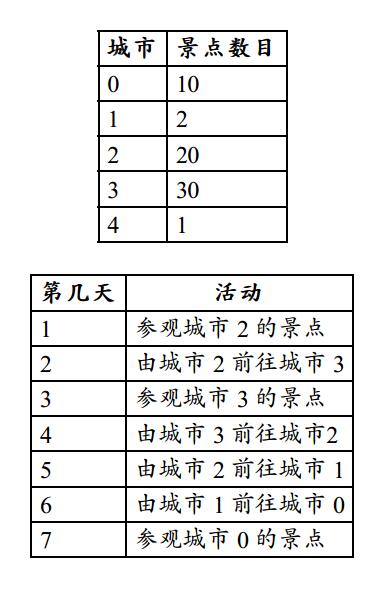
假设健佳有 7 天假期,有 5 个城市(参见下表),而且他由城市 2 开始。在第一天,健佳参
观城市2的 20 个景点。第二天,健佳由城市 2 去往城市 3。而在第三天,健佳参观城市 3 的
30 个景点。接下来的3天,健佳由城市 3 前往城市 0。而在第 7 天,健佳参观城市0的 10 个
景点。这样健佳参观的景点总数是20+30+10=60,这是他由城市 2 开始、在 7 天假期内最多
能参观的景点数目。
任务
请计算健佳最多可以参观多少个景点。
- n: 城市数。
- start: 起点城市的编号。
- d: 假期的天数。
- attraction: 长度为
n 的数组;attraction[i] 表示城市 i(0<=i<=n−1) 的景点数目。
Solution:
首先,我们先考虑最简单的一种情况,即子任务2,从0出发。
显然我们在这种情况下只会向一个方向前进,最终答案由最后的位置决定,因此我们枚举这个位置,然后路上花的时间
t
确定了,那么我们只需要求出从0到这个位置之间的城市中景点数前
至于子任务1,就算是使用
O(2n)
枚举选择的城市应该也是可以的,不再赘述。
然后,对于子任务3,就比较简单了。我们枚举左右到达的端点,再考虑是中->左->右还是中->右->左就好了,最大值可以用堆维护。复杂度
O(n2logn)
。
void solve(){
ll ans=0;
for(int l=s;l>=0;l--){
priority_queue<ll,vector<ll>,greater<ll> >Q;
ll sum=0;
for(int r=l;r<n;r++){
int k=d-(r-l)-(s-l);
if(k<=0)break;
sum+=A[r];
Q.push(A[r]);
if(r<s)continue;
if(k>=Q.size()){
if(sum>ans)ans=sum;
}else{
while(Q.size()>k){
sum-=Q.top();
Q.pop();
}
if(sum>ans)ans=sum;
}
}
}
for(int r=s;r<n;r++){
priority_queue<ll,vector<ll>,greater<ll> >Q;
ll sum=0;
for(int l=r;l>=0;l--){
int k=d-(r-l)-(r-s);
if(k<=0)break;
sum+=A[l];
Q.push(A[l]);
if(l>s)continue;
if(k>=Q.size()){
if(sum>ans)ans=sum;
}else{
while(Q.size()>k){
sum-=Q.top();
Q.pop();
}
if(sum>ans)ans=sum;
}
}
}
cout<<ans<<endl;
}然后我们来看正解的解法,首先我们能够发现一个单调性:
设
C[i]
表示向右花
i
天时间到达
可以证明:若
x<y
,则
C[x]<=C[y]
。
假设 c[x+1]<c[x] :
对于 x+1 :
在 [st,c[x+1]] 内选择 a=x+1−c[x+1] 个最多的景点总和 suma 大于在 [st,c[x]] 内选择 b=x+1−c[x] 个最多的景点总和 sumb .
设 A[i] 为在 [st,c[x+1]] 中第 i 大的数,B[i] 为 [st,c[x]] 中第 i 大的数.
因为[st,c[x]] 包含 [st,c[x+1]] ,所以 B[i]≥A[i] . 因为 c[x+1]<c[x] ,所以 a>b .
又因为 A,B 都是单调递减的序列,所以 suma−A[a]≥sumb−B[b] .
即在 [st,c[x+1]] 内选择 x−c[x+1] 个最多的景点和 suma−A[a] 大于等于在 [st,c[x]] 中选择 x−c[x] 个最多的景点和 sumb−B[b] .
所以对于 x 来说c[x+1] 比 c[x] 更优,那么对 x 最优的决策点就不是c[x] 了.所以 c[x] 随 x 变化的单调性是成立的.
By LINSY
因此,我们考虑分治,对于左端点
最后,我们只需要求出
C[mid]
即可,我们可以直接循环遍历右端点的区间,就可以得到能够用来观光的时间,然后求区间前k大值的和,则可以用主席树。
于是问题就被解决了,复杂度
O(nlog2n)
。
#include<stdio.h>
#include<iostream>
#include<algorithm>
#define LL long long
#define M 100005
#define MLOGM 2000000
using namespace std;
LL sum[MLOGM],ans=0;
int Lson[MLOGM],Rson[MLOGM],cnt[MLOGM],tot=0,A[M],B[M],rt[MLOGM];
int n,m,st,d;
void build(int L,int R,int &tid){
tid=++tot;
sum[tid]=cnt[tid]=0;
if(L==R)return;
int mid=(L+R)>>1;
build(L,mid,Lson[tid]);
build(mid+1,R,Rson[tid]);
}
void insert(int od,int &tid,int L,int R,int x){
tid=++tot;
Lson[tid]=Lson[od];
Rson[tid]=Rson[od];
cnt[tid]=cnt[od]+1;
sum[tid]=sum[od]+B[x];
if(L==R)return;
int mid=(L+R)>>1;
if(x<=mid)insert(Lson[od],Lson[tid],L,mid,x);
else insert(Rson[od],Rson[tid],mid+1,R,x);
}
LL query(int od,int id,int L,int R,int k){
if(cnt[id]-cnt[od]<=k)return sum[id]-sum[od];
if(L==R)return 1LL*B[L]*k;
int res=cnt[Rson[id]]-cnt[Rson[od]];
int mid=(L+R)>>1;
if(res>=k)return query(Rson[od],Rson[id],mid+1,R,k);
else return query(Rson[od],Rson[id],mid+1,R,res)+query(Lson[od],Lson[id],L,mid,k-res);
}
void solve(int ll,int lr,int rl,int rr){
if(ll>lr||rl>rr)return;
int mid=(ll+lr)>>1,x=rl;
LL res=0;
for(int i=rl;i<=rr;i++){
int rm=max(d-(st-mid)-(i-mid),d-(i-st)-(i-mid));
if(rm<=0)break;
LL rs=query(rt[mid-1],rt[i],0,m-1,rm);
if(rs>res){
x=i;res=rs;
}
}
if(res>ans)ans=res;
if(ll==lr)return;
solve(ll,mid-1,rl,x);
solve(mid+1,lr,x,rr);
}
int main(){
scanf("%d %d %d",&n,&st,&d);
st++;
for(int i=1;i<=n;i++){
scanf("%d",&A[i]);
B[i-1]=A[i];
}
sort(B,B+n);
m=unique(B,B+n)-B;
build(0,m-1,rt[0]);
for(int i=1;i<=n;i++){
A[i]=lower_bound(B,B+m,A[i])-B;
insert(rt[i-1],rt[i],0,m-1,A[i]);
}
solve(1,st,st,n);
cout<<ans<<endl;
return 0;
}























 1706
1706

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








