转载这一篇是为了与上一篇作对比:
一、误差准则函数与随机梯度下降:
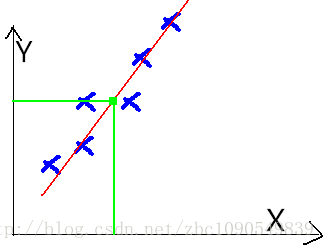
对于给定的一个点集(X,Y),找到一条曲线或者曲面,对其进行拟合之。同时称X中的变量为特征(Feature),Y值为预测值。
如图:
一个典型的机器学习的过程,首先给出一组输入数据X,我们的算法会通过一系列的过程得到一个估计的函数,这个函数有能力对没有见过的新数据给出一个新的估计Y,也被称为构建一个模型。
我们用X1、X2...Xn 去描述feature里面的分量,用Y来描述我们的估计,得到一下模型:
我们需要一种机制去评价这个模型对数据的描述到底够不够准确,而采集的数据x、y通常来说是存在误差的(多数情况下误差服从高斯分布),于是,自然的,引入误差函数:
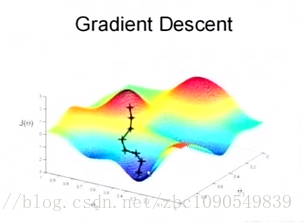
关键的一点是如何调整theta值,使误差函数J最小化。J函数构成一个曲面或者曲线,我们的目的是找到该曲面的最低点:
假设随机站在该曲面的一点,要以最快的速度到达最低点,我们当然会沿着坡度最大的方向往下走(梯度的反方向)
用数学描述就是一个求偏导数的过程:
这样,参数theta的更新过程描述为以下:
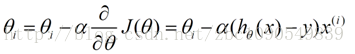
二、算法实现与测试:(相当于梯度下降,没有所谓的随机)
通过一组数据拟合 y = theta1*x1 +theta2*x2
- #Python 3.3.5
- # matrix_A 训练集
- matrix_A = [[1,4], [2,5], [5,1], [4,2]]
- Matrix_y = [19,26,19,20]
- theta = [2,5]
- #学习速率
- leraing_rate = 0.005
- loss = 50
- iters = 1
- Eps = 0.0001
- while loss>Eps and iters <1000 :
- loss = 0
- for i in range(3) :
- h = theta[0]*matrix_A[i][0] + theta[1]*matrix_A[i][1]
- theta[0] = theta[0] + leraing_rate*(Matrix_y[i]-h)*matrix_A[i][0]
- theta[1] = theta[1] + leraing_rate*(Matrix_y[i]-h)*matrix_A[i][1]
- for i in range(3) :
- Error = 0
- Error = theta[0]*matrix_A[i][0] + theta[1]*matrix_A[i][1] - Matrix_y[i]
- Error = Error*Error
- loss = loss +Error
- iters = iters +1
- print ('theta=',theta)
- print ('iters=',iters)
- >>>
- theta= [2.9980959216157945, 4.001522800837675]
- iters= 75
- matrix_A = [[1.05,4], [2.1,5], [5,1], [4,2]]
- >>>
- theta= [3.0095950685197725, 3.944718521027671]
- iters= 1000








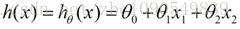
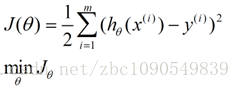
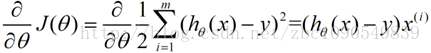














 1631
1631

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








